Đã trả lời bởi chuyên gia
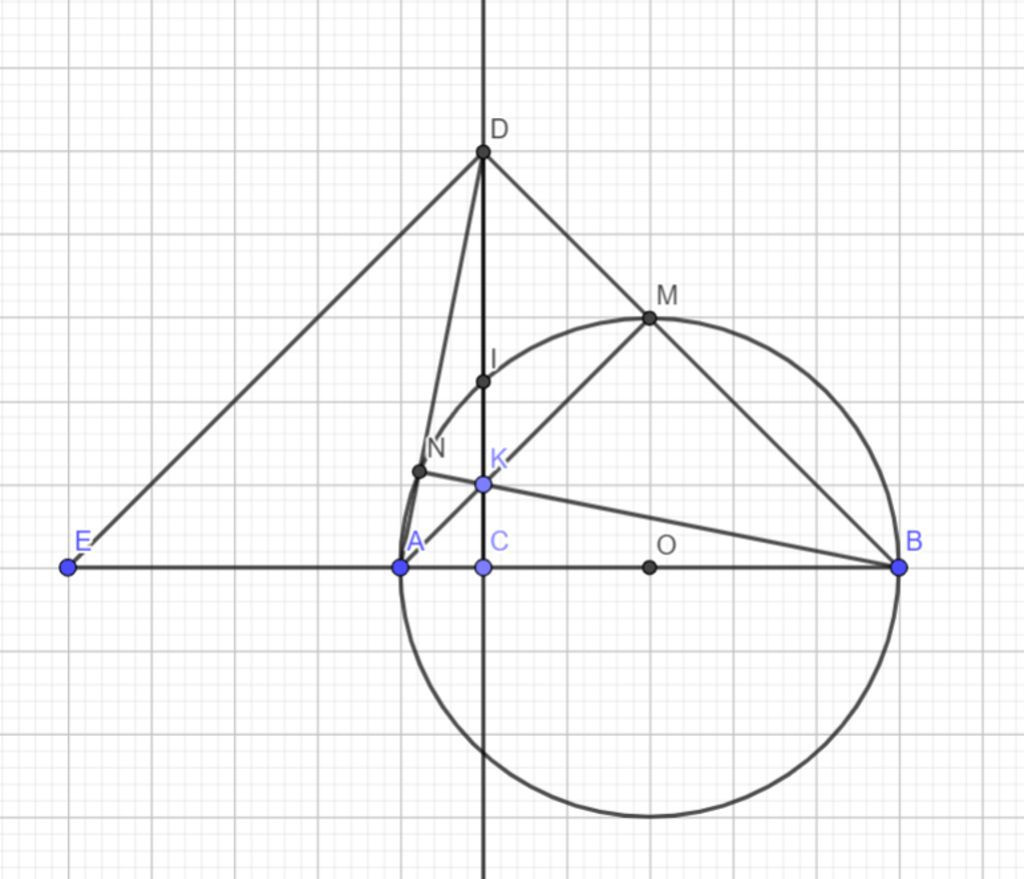
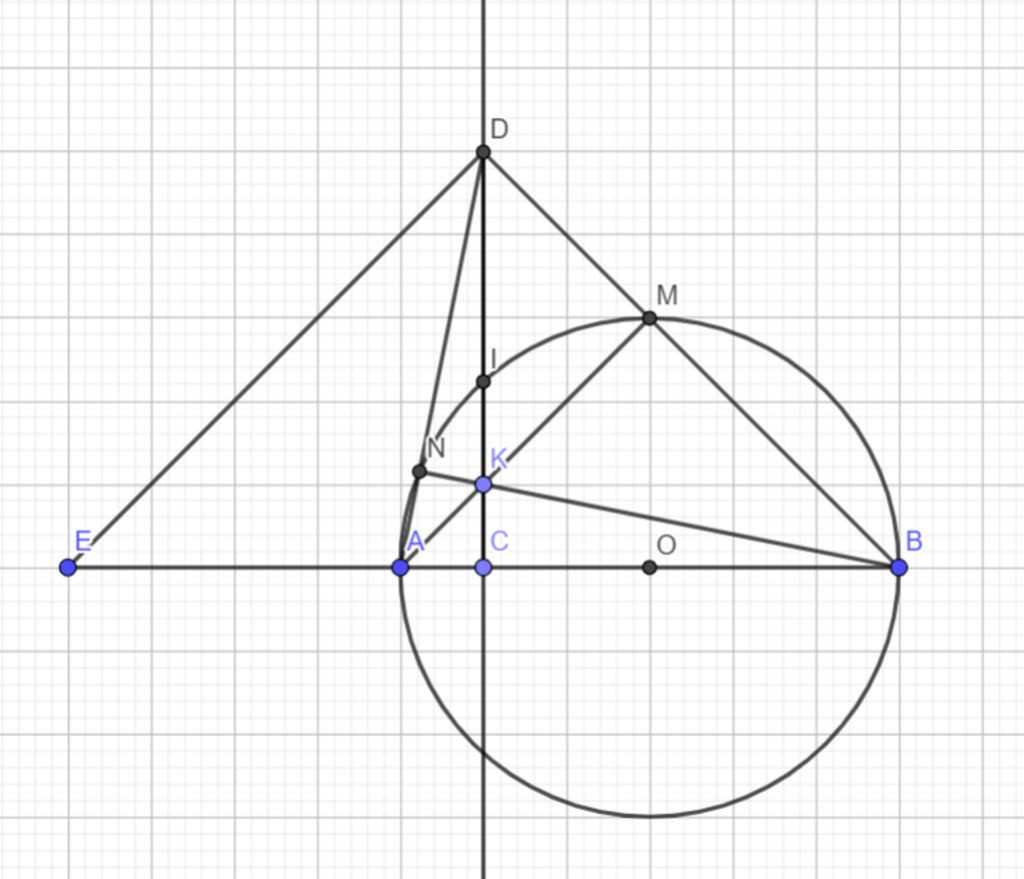
Cho nửa đường tròn tâm O đường kính AB, C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I, K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D.
Chứng minh :
a) Các tứ giác ACMD, BCKM nội tiếp đường tròn
b) CK.CD=CA.CB
c) Gọi N là giao điểm của AD và đường tròn O chứng minh B, K, N thẳng hàng
d) Tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định khi K di động trên đoạn thẳng CI
Quảng cáo
35 câu trả lời 105358
a. Ta có AB là đường kính của (O)→AM⊥MB
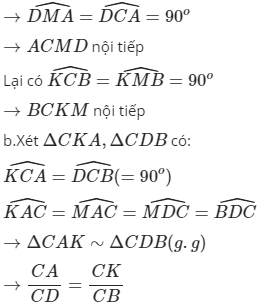
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
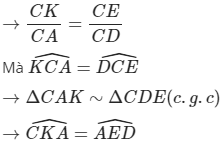
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
a.Ta có $AB$ là đường kính của $(O)\to AM\perp MB$
$\to \widehat{DMA}=\widehat{DCA}=90^o$
$\to ACMD$ nội tiếp
Lại có $\widehat{KCB}=\widehat{KMB}=90^o$
$\to BCKM$ nội tiếp
b.Xét $\Delta CKA, \Delta CDB$ có:
$\widehat{KCA}=\widehat{DCB}(=90^o)$
$\widehat{KAC}=\widehat{MAC}=\widehat{MDC}=\widehat{BDC}$
$\to\Delta CAK\sim\Delta CDB(g.g)$
$\to \dfrac{CA}{CD}=\dfrac{CK}{CB}$
$\to CK.CD=CA.CB$
c.Ta có $K\in(O)\to AN\perp NB\to BN\perp AD$
Vì $AM\perp BD, BN\perp AD, AM\cap BN=K\to K$ là trực tâm $\Delta DAB\to BK\perp AD$
$\to B, K, N$ thẳng hàng
d.Trên tia đối của tia $CB$ lấy điểm $E$ sao cho $CE=CB$
Ta có $CK.CD=CA.CB\to CK.CD=CA.CE$
$\to \dfrac{CK}{CA}=\dfrac{CE}{CD}$
Mà $\widehat{KCA}=\widehat{DCE}$
$\to\Delta CAK\sim\Delta CDE(c.g.c)$
$\to \widehat{CKA}=\widehat{AED}$
$\to AKDE$ nội tiếp
$\to E\in (AKD)$
$\to$Tâm đường tròn ngoại tiếp $\Delta AKD$ nằm trên trung trực $AE$ cố định
a. We have AB as the diameter of (O) → AM⊥MB
→ CK.CD=CA.CB
c. We have K∈(O)→AN⊥NB→BN⊥AD
Since AM⊥BD, BN⊥AD, AM∩BN={K} → K is orthocenter DAB
→BK⊥AD →B, K, N collinear
d. On the opposite ray of ray CB take point E such that CE=CB
We have CK.CD=CA.CB
→AKDE inline
→ E∈(AKD)
→ The center of the circumcircle ΔAKD lies on the orthocenter AE fixed
a. Ta có AB là đường kính của (O)→AM⊥MB
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
a. Ta có AB là đường kính của (O)→AM⊥MB
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
a. Ta có AB là đường kính của (O)→AM⊥MB
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
a. Ta có AB là đường kính của (O)→AM⊥MB
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
a. Ta có AB là đường kính của (O)→AM⊥MB
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
Đây ạ !
. Ta có AB là đường kính của (O)→AM⊥MB
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
a.Ta có ABAB là đường kính của (O)→AM⊥MB(O)→AM⊥MB
→ˆDMA=ˆDCA=90o→DMA^=DCA^=90o
→ACMD→ACMD nội tiếp
Lại có ˆKCB=ˆKMB=90oKCB^=KMB^=90o
→BCKM→BCKM nội tiếp
b.Xét ΔCKA,ΔCDBΔCKA,ΔCDB có:
ˆKCA=ˆDCB(=90o)KCA^=DCB^(=90o)
ˆKAC=ˆMAC=ˆMDC=ˆBDCKAC^=MAC^=MDC^=BDC^
→ΔCAK∼ΔCDB(g.g)→ΔCAK∼ΔCDB(g.g)
→CACD=CKCB→CACD=CKCB
→CK.CD=CA.CB→CK.CD=CA.CB
c.Ta có K∈(O)→AN⊥NB→BN⊥ADK∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD,BN⊥AD,AM∩BN=K→KAM⊥BD,BN⊥AD,AM∩BN=K→K là trực tâm ΔDAB→BK⊥ADΔDAB→BK⊥AD
→B,K,N→B,K,N thẳng hàng
d.Trên tia đối của tia CBCB lấy điểm EE sao cho CE=CBCE=CB
Ta có CK.CD=CA.CB→CK.CD=CA.CECK.CD=CA.CB→CK.CD=CA.CE
→CKCA=CECD→CKCA=CECD
Mà ˆKCA=ˆDCEKCA^=DCE^
→ΔCAK∼ΔCDE(c.g.c)→ΔCAK∼ΔCDE(c.g.c)
→ˆCKA=ˆAED→CKA^=AED^
→AKDE→AKDE nội tiếp
→E∈(AKD)→E∈(AKD)
→→Tâm đường tròn ngoại tiếp ΔAKDΔAKD nằm trên trung trực AEAE cố định
a.Ta có ABAB là đường kính của (O)→AM⊥MB(O)→AM⊥MB
→ˆDMA=ˆDCA=90o→DMA^=DCA^=90o
→ACMD→ACMD nội tiếp
Lại có ˆKCB=ˆKMB=90oKCB^=KMB^=90o
→BCKM→BCKM nội tiếp
b.Xét ΔCKA,ΔCDBΔCKA,ΔCDB có:
ˆKCA=ˆDCB(=90o)KCA^=DCB^(=90o)
ˆKAC=ˆMAC=ˆMDC=ˆBDCKAC^=MAC^=MDC^=BDC^
→ΔCAK∼ΔCDB(g.g)→ΔCAK∼ΔCDB(g.g)
→CACD=CKCB→CACD=CKCB
→CK.CD=CA.CB→CK.CD=CA.CB
c.Ta có K∈(O)→AN⊥NB→BN⊥ADK∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD,BN⊥AD,AM∩BN=K→KAM⊥BD,BN⊥AD,AM∩BN=K→K là trực tâm ΔDAB→BK⊥ADΔDAB→BK⊥AD
→B,K,N→B,K,N thẳng hàng
d.Trên tia đối của tia CBCB lấy điểm EE sao cho CE=CBCE=CB
Ta có CK.CD=CA.CB→CK.CD=CA.CECK.CD=CA.CB→CK.CD=CA.CE
→CKCA=CECD→CKCA=CECD
Mà ˆKCA=ˆDCEKCA^=DCE^
→ΔCAK∼ΔCDE(c.g.c)→ΔCAK∼ΔCDE(c.g.c)
→ˆCKA=ˆAED→CKA^=AED^
→AKDE→AKDE nội tiếp
→E∈(AKD)→E∈(AKD)
→→Tâm đường tròn ngoại tiếp ΔAKDΔAKD nằm trên trung trực AEAE cố định
a. We have AB as the diameter of (O) → AM⊥MB
→ CK.CD=CA.CB
c. We have K∈(O)→AN⊥NB→BN⊥AD
Since AM⊥BD, BN⊥AD, AM∩BN={K} → K is orthocenter DAB
→BK⊥AD →B, K, N collinear
d. On the opposite ray of ray CB take point E such that CE=CB
We have CK.CD=CA.CB
→AKDE inline
→ E∈(AKD)
→ The center of the circumcircle ΔAKD lies on the orthocenter AE fixed
a.Ta có ABAB là đường kính của (O)→AM⊥MB(O)→AM⊥MB
→ˆDMA=ˆDCA=90o→DMA^=DCA^=90o
→ACMD→ACMD nội tiếp
Lại có ˆKCB=ˆKMB=90oKCB^=KMB^=90o
→BCKM→BCKM nội tiếp
a. Ta có AB là đường kính của (O)→AM⊥MB
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
a. We have AB as the diameter of (O) → AM⊥MB
→ CK.CD=CA.CB
c. We have K∈(O)→AN⊥NB→BN⊥AD
Since AM⊥BD, BN⊥AD, AM∩BN={K} → K is orthocenter DAB
→BK⊥AD →B, K, N collinear
d. On the opposite ray of ray CB take point E such that CE=CB
We have CK.CD=CA.CB
→AKDE inline
→ E∈(AKD)
→ The center of the circumcircle ΔAKD lies on the orthocenter AE fixed
a. Ta có AB là đường kính của (O)→AM⊥MB
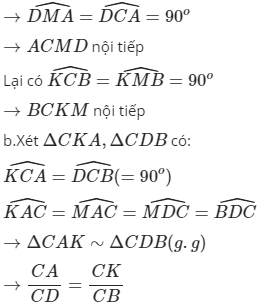
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
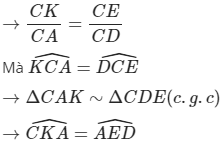
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
a.Ta có AB�� là đường kính của (O)→AM⊥MB(�)→��⊥��
→ˆDMA=ˆDCA=90o→���^=���^=90�
→ACMD→���� nội tiếp
Lại có ˆKCB=ˆKMB=90o���^=���^=90�
→BCKM→���� nội tiếp
b.Xét ΔCKA,ΔCDBΔ���,Δ��� có:
ˆKCA=ˆDCB(=90o)���^=���^(=90�)
ˆKAC=ˆMAC=ˆMDC=ˆBDC���^=���^=���^=���^
→ΔCAK∼ΔCDB(g.g)→Δ���∼Δ���(�.�)
→CACD=CKCB→����=����
→CK.CD=CA.CB→��.��=��.��
c.Ta có K∈(O)→AN⊥NB→BN⊥AD�∈(�)→��⊥��→��⊥��
Vì AM⊥BD,BN⊥AD,AM∩BN=K→K��⊥��,��⊥��,��∩��=�→� là trực tâm ΔDAB→BK⊥ADΔ���→��⊥��
→B,K,N→�,�,� thẳng hàng
d.Trên tia đối của tia CB�� lấy điểm E� sao cho CE=CB��=��
Ta có CK.CD=CA.CB→CK.CD=CA.CE��.��=��.��→��.��=��.��
→CKCA=CECD→����=����
Mà ˆKCA=ˆDCE���^=���^
→ΔCAK∼ΔCDE(c.g.c)→Δ���∼Δ���(�.�.�)
→ˆCKA=ˆAED→���^=���^
→AKDE→���� nội tiếp
→E∈(AKD)→�∈(���)
→→Tâm đường tròn ngoại tiếp ΔAKDΔ��� nằm trên trung trực AE�� cố định
a. We have AB as the diameter of (O) → AM⊥MB
→ CK.CD=CA.CB
c. We have K∈(O)→AN⊥NB→BN⊥AD
Since AM⊥BD, BN⊥AD, AM∩BN={K} → K is orthocenter DAB
→BK⊥AD →B, K, N collinear
d. On the opposite ray of ray CB take point E such that CE=CB
We have CK.CD=CA.CB
→AKDE inline
→ E∈(AKD)
→ The center of the circumcircle ΔAKD lies on the orthocenter AE fixed
a. Ta có AB là đường kính của (O)→AM⊥MB
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
a.Ta có AB𝐴𝐵 là đường kính của (O)→AM⊥MB(𝑂)→𝐴𝑀⊥𝑀𝐵
→ˆDMA=ˆDCA=90o→𝐷𝑀𝐴^=𝐷𝐶𝐴^=90𝑜
→ACMD→𝐴𝐶𝑀𝐷 nội tiếp
Lại có ˆKCB=ˆKMB=90o𝐾𝐶𝐵^=𝐾𝑀𝐵^=90𝑜
→BCKM→𝐵𝐶𝐾𝑀 nội tiếp
b.Xét ΔCKA,ΔCDBΔ𝐶𝐾𝐴,Δ𝐶𝐷𝐵 có:
ˆKCA=ˆDCB(=90o)𝐾𝐶𝐴^=𝐷𝐶𝐵^(=90𝑜)
ˆKAC=ˆMAC=ˆMDC=ˆBDC𝐾𝐴𝐶^=𝑀𝐴𝐶^=𝑀𝐷𝐶^=𝐵𝐷𝐶^
→ΔCAK∼ΔCDB(g.g)→Δ𝐶𝐴𝐾∼Δ𝐶𝐷𝐵(𝑔.𝑔)
→CACD=CKCB→𝐶𝐴𝐶𝐷=𝐶𝐾𝐶𝐵
→CK.CD=CA.CB→𝐶𝐾.𝐶𝐷=𝐶𝐴.𝐶𝐵
c.Ta có K∈(O)→AN⊥NB→BN⊥AD𝐾∈(𝑂)→𝐴𝑁⊥𝑁𝐵→𝐵𝑁⊥𝐴𝐷
Vì AM⊥BD,BN⊥AD,AM∩BN=K→K𝐴𝑀⊥𝐵𝐷,𝐵𝑁⊥𝐴𝐷,𝐴𝑀∩𝐵𝑁=𝐾→𝐾 là trực tâm ΔDAB→BK⊥ADΔ𝐷𝐴𝐵→𝐵𝐾⊥𝐴𝐷
→B,K,N→𝐵,𝐾,𝑁 thẳng hàng
d.Trên tia đối của tia CB𝐶𝐵 lấy điểm E𝐸 sao cho CE=CB𝐶𝐸=𝐶𝐵
Ta có CK.CD=CA.CB→CK.CD=CA.CE𝐶𝐾.𝐶𝐷=𝐶𝐴.𝐶𝐵→𝐶𝐾.𝐶𝐷=𝐶𝐴.𝐶𝐸
→CKCA=CECD→𝐶𝐾𝐶𝐴=𝐶𝐸𝐶𝐷
Mà ˆKCA=ˆDCE𝐾𝐶𝐴^=𝐷𝐶𝐸^
→ΔCAK∼ΔCDE(c.g.c)→Δ𝐶𝐴𝐾∼Δ𝐶𝐷𝐸(𝑐.𝑔.𝑐)
→ˆCKA=ˆAED→𝐶𝐾𝐴^=𝐴𝐸𝐷^
→AKDE→𝐴𝐾𝐷𝐸 nội tiếp
→E∈(AKD)→𝐸∈(𝐴𝐾𝐷)
→→Tâm đường tròn ngoại tiếp ΔAKDΔ𝐴𝐾𝐷 nằm trên trung trực AE𝐴𝐸 cố định
a.Ta có AB�� là đường kính của (O)→AM⊥MB(�)→��⊥��
→ˆDMA=ˆDCA=90o→���^=���^=90�
→ACMD→���� nội tiếp
Lại có ˆKCB=ˆKMB=90o���^=���^=90�
→BCKM→���� nội tiếp
b.Xét ΔCKA,ΔCDBΔ���,Δ��� có:
ˆKCA=ˆDCB(=90o)���^=���^(=90�)
ˆKAC=ˆMAC=ˆMDC=ˆBDC���^=���^=���^=���^
→ΔCAK∼ΔCDB(g.g)→Δ���∼Δ���(�.�)
→CACD=CKCB→����=����
→CK.CD=CA.CB→��.��=��.��
c.Ta có K∈(O)→AN⊥NB→BN⊥AD�∈(�)→��⊥��→��⊥��
Vì AM⊥BD,BN⊥AD,AM∩BN=K→K��⊥��,��⊥��,��∩��=�→� là trực tâm ΔDAB→BK⊥ADΔ���→��⊥��
→B,K,N→�,�,� thẳng hàng
d.Trên tia đối của tia CB�� lấy điểm E� sao cho CE=CB��=��
Ta có CK.CD=CA.CB→CK.CD=CA.CE��.��=��.��→��.��=��.��
→CKCA=CECD→����=����
Mà ˆKCA=ˆDCE���^=���^
→ΔCAK∼ΔCDE(c.g.c)→Δ���∼Δ���(�.�.�)
→ˆCKA=ˆAED→���^=���^
→AKDE→���� nội tiếp
→E∈(AKD)→�∈(���)
→→Tâm đường tròn ngoại tiếp ΔAKDΔ��� nằm trên trung trực AE�� cố định
a.Ta có AB là đường kính của (O)→AM⊥MB
→ˆDMA=ˆDCA=90o
→ACMD nội tiếp
Lại có ˆKCB=ˆKMB=90o
→BCKM nội tiếp
b.Xét ΔCKA,ΔCDB có:
ˆKCA=ˆDCB(=90o)
ˆKAC=ˆMAC=ˆMDC=ˆBDC
→ΔCAK∼ΔCDB(g.g)
→CACD=CKCB
→CK.CD=CA.CB
c.Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD,BN⊥AD,AM∩BN=K→K là trực tâm ΔDAB→BK⊥AD
→B,K,N thẳng hàng
d.Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB→CK.CD=CA.CE
→CKCA=CECD
Mà ˆKCA=ˆDCE
→ΔCAK∼ΔCDE(c.g.c)
→ˆCKA=ˆAED
→AKDE nội tiếp
→E∈(AKD)
→Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
a) Các tứ giác ACMD, BCKM nội tiếp đường tròn
Step 1: Chứng minh tứ giác ACMD nội tiếp
Góc ∠ACB=90∘angle cap A cap C cap B equals 90 raised to the composed with power
∠𝐴𝐶𝐵=90∘
(do CI⟂ABcap C cap I ⟂ cap A cap B
𝐶𝐼⟂𝐴𝐵
tại Ccap C
𝐶
).
Góc ∠AMB=90∘angle cap A cap M cap B equals 90 raised to the composed with power
∠𝐴𝑀𝐵=90∘
(góc nội tiếp chắn nửa đường tròn đường kính ABcap A cap B
𝐴𝐵
).
Do Mcap M
𝑀
nằm trên nửa đường tròn, ∠AMBangle cap A cap M cap B
∠𝐴𝑀𝐵
là góc vuông, suy ra AM⟂MBcap A cap M ⟂ cap M cap B
𝐴𝑀⟂𝑀𝐵
. Dcap D
𝐷
nằm trên tia BMcap B cap M
𝐵𝑀
, nên AM⟂BDcap A cap M ⟂ cap B cap D
𝐴𝑀⟂𝐵𝐷
.
Trong tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
, AC⟂BDcap A cap C ⟂ cap B cap D
𝐴𝐶⟂𝐵𝐷
(do Ccap C
𝐶
nằm trên ABcap A cap B
𝐴𝐵
và CI⟂ABcap C cap I ⟂ cap A cap B
𝐶𝐼⟂𝐴𝐵
, Dcap D
𝐷
nằm trên đường thẳng CIcap C cap I
𝐶𝐼
) và DM⟂ABcap D cap M ⟂ cap A cap B
𝐷𝑀⟂𝐴𝐵
(do Mcap M
𝑀
nằm trên nửa đường tròn).
Kcap K
𝐾
nằm trên CIcap C cap I
𝐶𝐼
, Dcap D
𝐷
nằm trên CIcap C cap I
𝐶𝐼
.
CI⟂ABcap C cap I ⟂ cap A cap B
𝐶𝐼⟂𝐴𝐵
tại Ccap C
𝐶
nên ∠ACD=90∘angle cap A cap C cap D equals 90 raised to the composed with power
∠𝐴𝐶𝐷=90∘
.
∠AMD=90∘angle cap A cap M cap D equals 90 raised to the composed with power
∠𝐴𝑀𝐷=90∘
(do ∠AMB=90∘angle cap A cap M cap B equals 90 raised to the composed with power
∠𝐴𝑀𝐵=90∘
và Dcap D
𝐷
thuộc BMcap B cap M
𝐵𝑀
).
Tứ giác ACMDcap A cap C cap M cap D
𝐴𝐶𝑀𝐷
có ∠ACD+∠AMD=90∘+90∘=180∘angle cap A cap C cap D plus angle cap A cap M cap D equals 90 raised to the composed with power plus 90 raised to the composed with power equals 180 raised to the composed with power
∠𝐴𝐶𝐷+∠𝐴𝑀𝐷=90∘+90∘=180∘
.
Tổng hai góc đối bằng 180∘180 raised to the composed with power
180∘
nên tứ giác ACMDcap A cap C cap M cap D
𝐴𝐶𝑀𝐷
nội tiếp đường tròn.
Step 2: Chứng minh tứ giác BCKM nội tiếp
Góc ∠BCK=90∘angle cap B cap C cap K equals 90 raised to the composed with power
∠𝐵𝐶𝐾=90∘
(do CI⟂ABcap C cap I ⟂ cap A cap B
𝐶𝐼⟂𝐴𝐵
tại Ccap C
𝐶
).
Góc ∠BMK=90∘angle cap B cap M cap K equals 90 raised to the composed with power
∠𝐵𝑀𝐾=90∘
(do ∠BMA=90∘angle cap B cap M cap A equals 90 raised to the composed with power
∠𝐵𝑀𝐴=90∘
và Kcap K
𝐾
nằm trên ADcap A cap D
𝐴𝐷
).
À không, Kcap K
𝐾
nằm trên CIcap C cap I
𝐶𝐼
.
∠BCK=90∘angle cap B cap C cap K equals 90 raised to the composed with power
∠𝐵𝐶𝐾=90∘
Góc ∠AMB=90∘angle cap A cap M cap B equals 90 raised to the composed with power
∠𝐴𝑀𝐵=90∘
, suy ra AM⟂BMcap A cap M ⟂ cap B cap M
𝐴𝑀⟂𝐵𝑀
.
Trong tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
, AMcap A cap M
𝐴𝑀
là đường cao thứ nhất, DCcap D cap C
𝐷𝐶
là đường cao thứ hai. Kcap K
𝐾
là trực tâm của tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
.
Do Kcap K
𝐾
là trực tâm, BK⟂ADcap B cap K ⟂ cap A cap D
𝐵𝐾⟂𝐴𝐷
.
Góc ∠BKN=90∘angle cap B cap K cap N equals 90 raised to the composed with power
∠𝐵𝐾𝑁=90∘
(do B,K,Ncap B comma cap K comma cap N
𝐵,𝐾,𝑁
thẳng hàng và AD⟂BKcap A cap D ⟂ cap B cap K
𝐴𝐷⟂𝐵𝐾
).
Góc ∠BKM=90∘angle cap B cap K cap M equals 90 raised to the composed with power
∠𝐵𝐾𝑀=90∘
(do BK⟂ADcap B cap K ⟂ cap A cap D
𝐵𝐾⟂𝐴𝐷
và Mcap M
𝑀
nằm trên ADcap A cap D
𝐴𝐷
).
Tứ giác BCKMcap B cap C cap K cap M
𝐵𝐶𝐾𝑀
có ∠BCK=90∘angle cap B cap C cap K equals 90 raised to the composed with power
∠𝐵𝐶𝐾=90∘
và ∠BMK=90∘angle cap B cap M cap K equals 90 raised to the composed with power
∠𝐵𝑀𝐾=90∘
.
Hai đỉnh Ccap C
𝐶
và Mcap M
𝑀
cùng nhìn cạnh BKcap B cap K
𝐵𝐾
dưới một góc 90∘90 raised to the composed with power
90∘
nên tứ giác BCKMcap B cap C cap K cap M
𝐵𝐶𝐾𝑀
nội tiếp đường tròn đường kính BKcap B cap K
𝐵𝐾
.
Answer:
Tứ giác ACMDcap A cap C cap M cap D
𝐴𝐶𝑀𝐷
có ∠ACD=90∘angle cap A cap C cap D equals 90 raised to the composed with power
∠𝐴𝐶𝐷=90∘
và ∠AMD=90∘angle cap A cap M cap D equals 90 raised to the composed with power
∠𝐴𝑀𝐷=90∘
, tổng hai góc đối bằng 180∘180 raised to the composed with power
180∘
nên tứ giác ACMD nội tiếp đường tròn. Tứ giác BCKMcap B cap C cap K cap M
𝐵𝐶𝐾𝑀
có ∠BCK=90∘angle cap B cap C cap K equals 90 raised to the composed with power
∠𝐵𝐶𝐾=90∘
và ∠BMK=90∘angle cap B cap M cap K equals 90 raised to the composed with power
∠𝐵𝑀𝐾=90∘
, hai đỉnh C,Mcap C comma cap M
𝐶,𝑀
cùng nhìn cạnh BKcap B cap K
𝐵𝐾
dưới góc 90∘90 raised to the composed with power
90∘
nên tứ giác BCKM nội tiếp đường tròn.
b) CK.CD=CA.CB
Step 1: Sử dụng hệ thức lượng trong tam giác vuông
Trong tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
vuông tại Acap A
𝐴
(không đúng, tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
không vuông tại Acap A
𝐴
).
Ta có CI⟂ABcap C cap I ⟂ cap A cap B
𝐶𝐼⟂𝐴𝐵
, nên ∠ACB=90∘angle cap A cap C cap B equals 90 raised to the composed with power
∠𝐴𝐶𝐵=90∘
(không đúng, ∠ACBangle cap A cap C cap B
∠𝐴𝐶𝐵
không nhất thiết là 90∘90 raised to the composed with power
90∘
). CI⟂ABcap C cap I ⟂ cap A cap B
𝐶𝐼⟂𝐴𝐵
tại Ccap C
𝐶
.
Trong tam giác ABDcap A cap B cap D
𝐴𝐵𝐷
, DC⟂ABcap D cap C ⟂ cap A cap B
𝐷𝐶⟂𝐴𝐵
tại Ccap C
𝐶
. AM⟂BDcap A cap M ⟂ cap B cap D
𝐴𝑀⟂𝐵𝐷
tại Mcap M
𝑀
. Kcap K
𝐾
là giao điểm của AMcap A cap M
𝐴𝑀
và DCcap D cap C
𝐷𝐶
, nên Kcap K
𝐾
là trực tâm. BK⟂ADcap B cap K ⟂ cap A cap D
𝐵𝐾⟂𝐴𝐷
.
Xét tam giác ACDcap A cap C cap D
𝐴𝐶𝐷
vuông tại Ccap C
𝐶
.
Xét tam giác BCKcap B cap C cap K
𝐵𝐶𝐾
vuông tại Ccap C
𝐶
.
Xét tam giác ADBcap A cap D cap B
𝐴𝐷𝐵
có đường cao DCcap D cap C
𝐷𝐶
.
Xét tam giác ACBcap A cap C cap B
𝐴𝐶𝐵
có đường cao CIcap C cap I
𝐶𝐼
.
Sử dụng tứ giác ACMDcap A cap C cap M cap D
𝐴𝐶𝑀𝐷
nội tiếp, ta có △ACK∼△DCBtriangle cap A cap C cap K tilde triangle cap D cap C cap B
△𝐴𝐶𝐾∼△𝐷𝐶𝐵
(không đúng).
Xét △ACKtriangle cap A cap C cap K
△𝐴𝐶𝐾
và △DCBtriangle cap D cap C cap B
△𝐷𝐶𝐵
.
Góc ∠KAC=∠KDCangle cap K cap A cap C equals angle cap K cap D cap C
∠𝐾𝐴𝐶=∠𝐾𝐷𝐶
(không đúng).
Xét hai tam giác vuông △ACKtriangle cap A cap C cap K
△𝐴𝐶𝐾
và △DCBtriangle cap D cap C cap B
△𝐷𝐶𝐵
(không đúng, chúng không vuông).
Sử dụng hệ thức lượng trong tam giác ADBcap A cap D cap B
𝐴𝐷𝐵
với đường cao DCcap D cap C
𝐷𝐶
. CD2=CA⋅CBcap C cap D squared equals cap C cap A center dot cap C cap B
𝐶𝐷2=𝐶𝐴⋅𝐶𝐵
(không đúng, chỉ đúng nếu △ADBtriangle cap A cap D cap B
△𝐴𝐷𝐵
vuông tại Dcap D
𝐷
).
Sử dụng tam giác đồng dạng: △ACK∼△BCDtriangle cap A cap C cap K tilde triangle cap B cap C cap D
△𝐴𝐶𝐾∼△𝐵𝐶𝐷
(không đúng).
Xét △ACKtriangle cap A cap C cap K
△𝐴𝐶𝐾
và △DCBtriangle cap D cap C cap B
△𝐷𝐶𝐵
(không đúng).
Xét △AKCtriangle cap A cap K cap C
△𝐴𝐾𝐶
và △DBCtriangle cap D cap B cap C
△𝐷𝐵𝐶
. ∠ACK=∠DCB=90∘angle cap A cap C cap K equals angle cap D cap C cap B equals 90 raised to the composed with power
∠𝐴𝐶𝐾=∠𝐷𝐶𝐵=90∘
. ∠KAC=∠CDBangle cap K cap A cap C equals angle cap C cap D cap B
∠𝐾𝐴𝐶=∠𝐶𝐷𝐵
(cùng phụ với ∠ABDangle cap A cap B cap D
∠𝐴𝐵𝐷
).
Vậy △AKC∼△DBCtriangle cap A cap K cap C tilde triangle cap D cap B cap C
△𝐴𝐾𝐶∼△𝐷𝐵𝐶
(g.g).
Tỉ số đồng dạng: AKDB=KCBC=ACDCthe fraction with numerator cap A cap K and denominator cap D cap B end-fraction equals the fraction with numerator cap K cap C and denominator cap B cap C end-fraction equals the fraction with numerator cap A cap C and denominator cap D cap C end-fraction
𝐴𝐾𝐷𝐵=𝐾𝐶𝐵𝐶=𝐴𝐶𝐷𝐶
.
Từ KCBC=ACDCthe fraction with numerator cap K cap C and denominator cap B cap C end-fraction equals the fraction with numerator cap A cap C and denominator cap D cap C end-fraction
𝐾𝐶𝐵𝐶=𝐴𝐶𝐷𝐶
, suy ra KC⋅DC=AC⋅BCcap K cap C center dot cap D cap C equals cap A cap C center dot cap B cap C
𝐾𝐶⋅𝐷𝐶=𝐴𝐶⋅𝐵𝐶
, hay CK⋅CD=CA⋅CBcap C cap K center dot cap C cap D equals cap C cap A center dot cap C cap B
𝐶𝐾⋅𝐶𝐷=𝐶𝐴⋅𝐶𝐵
.
Answer:
Xét △AKCtriangle cap A cap K cap C
△𝐴𝐾𝐶
và △DBCtriangle cap D cap B cap C
△𝐷𝐵𝐶
, có ∠ACK=∠DCB=90∘angle cap A cap C cap K equals angle cap D cap C cap B equals 90 raised to the composed with power
∠𝐴𝐶𝐾=∠𝐷𝐶𝐵=90∘
và ∠KAC=∠CDBangle cap K cap A cap C equals angle cap C cap D cap B
∠𝐾𝐴𝐶=∠𝐶𝐷𝐵
(cùng phụ với ∠ABCangle cap A cap B cap C
∠𝐴𝐵𝐶
). Do đó, △AKC∼△DBCtriangle cap A cap K cap C tilde triangle cap D cap B cap C
△𝐴𝐾𝐶∼△𝐷𝐵𝐶
(g.g). Từ tính chất tam giác đồng dạng, ta có tỉ số KCBC=ACDCthe fraction with numerator cap K cap C and denominator cap B cap C end-fraction equals the fraction with numerator cap A cap C and denominator cap D cap C end-fraction
𝐾𝐶𝐵𝐶=𝐴𝐶𝐷𝐶
, suy ra CK⋅CD=CA⋅CBcap C cap K center dot cap C cap D equals cap C cap A center dot cap C cap B
𝐶𝐾⋅𝐶𝐷=𝐶𝐴⋅𝐶𝐵
.
c) Gọi N là giao điểm của AD và đường tròn O chứng minh B, K, N thẳng hàng
Step 1: Sử dụng tính chất góc nội tiếp và trực tâm
Ncap N
𝑁
là giao điểm của ADcap A cap D
𝐴𝐷
và đường tròn (O)open paren cap O close paren
(𝑂)
.
Góc ∠ANB=90∘angle cap A cap N cap B equals 90 raised to the composed with power
∠𝐴𝑁𝐵=90∘
(góc nội tiếp chắn nửa đường tròn đường kính ABcap A cap B
𝐴𝐵
).
Suy ra BN⟂ADcap B cap N ⟂ cap A cap D
𝐵𝑁⟂𝐴𝐷
.
Ở phần a) đã chứng minh Kcap K
𝐾
là trực tâm của △ABDtriangle cap A cap B cap D
△𝐴𝐵𝐷
, nên BK⟂ADcap B cap K ⟂ cap A cap D
𝐵𝐾⟂𝐴𝐷
.
Cả BNcap B cap N
𝐵𝑁
và BKcap B cap K
𝐵𝐾
đều vuông góc với ADcap A cap D
𝐴𝐷
tại cùng một điểm Ncap N
𝑁
(hoặc Kcap K
𝐾
).
Do đó, ba điểm B,K,Ncap B comma cap K comma cap N
𝐵,𝐾,𝑁
phải thẳng hàng.
Answer:
Ncap N
𝑁
là giao điểm của ADcap A cap D
𝐴𝐷
và đường tròn (O)open paren cap O close paren
(𝑂)
, nên ∠ANB=90∘angle cap A cap N cap B equals 90 raised to the composed with power
∠𝐴𝑁𝐵=90∘
(góc nội tiếp chắn nửa đường tròn), suy ra BN⟂ADcap B cap N ⟂ cap A cap D
𝐵𝑁⟂𝐴𝐷
. Đã chứng minh Kcap K
𝐾
là trực tâm của △ABDtriangle cap A cap B cap D
△𝐴𝐵𝐷
, nên BK⟂ADcap B cap K ⟂ cap A cap D
𝐵𝐾⟂𝐴𝐷
. Vì BNcap B cap N
𝐵𝑁
và BKcap B cap K
𝐵𝐾
cùng vuông góc với ADcap A cap D
𝐴𝐷
, B,K,Ncap B comma cap K comma cap N
𝐵,𝐾,𝑁
thẳng hàng.
d) Tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định khi K di động trên đoạn thẳng CI
Step 1: Tìm tâm đường tròn ngoại tiếp tam giác AKD
Gọi O′cap O prime
𝑂′
là tâm đường tròn ngoại tiếp △AKDtriangle cap A cap K cap D
△𝐴𝐾𝐷
.
△AKDtriangle cap A cap K cap D
△𝐴𝐾𝐷
có ∠AKD=∠NKCangle cap A cap K cap D equals angle cap N cap K cap C
∠𝐴𝐾𝐷=∠𝑁𝐾𝐶
.
BK⟂ADcap B cap K ⟂ cap A cap D
𝐵𝐾⟂𝐴𝐷
, nên ∠BKD=90∘angle cap B cap K cap D equals 90 raised to the composed with power
∠𝐵𝐾𝐷=90∘
.
ACMDcap A cap C cap M cap D
𝐴𝐶𝑀𝐷
nội tiếp, BCKMcap B cap C cap K cap M
𝐵𝐶𝐾𝑀
nội tiếp.
Góc ∠ADK=∠ABKangle cap A cap D cap K equals angle cap A cap B cap K
∠𝐴𝐷𝐾=∠𝐴𝐵𝐾
(không đúng).
Tâm O′cap O prime
𝑂′
là giao điểm của các đường trung trực của AK,KD,ADcap A cap K comma cap K cap D comma cap A cap D
𝐴𝐾,𝐾𝐷,𝐴𝐷
.
Gọi M′cap M prime
𝑀′
là trung điểm của ADcap A cap D
𝐴𝐷
. Đường trung trực của ADcap A cap D
𝐴𝐷
đi qua O′cap O prime
𝑂′
và vuông góc với ADcap A cap D
𝐴𝐷
.
Ta biết BK⟂ADcap B cap K ⟂ cap A cap D
𝐵𝐾⟂𝐴𝐷
. Đường trung trực của ADcap A cap D
𝐴𝐷
song song với BKcap B cap K
𝐵𝐾
.
CK⋅CD=CA⋅CBcap C cap K center dot cap C cap D equals cap C cap A center dot cap C cap B
𝐶𝐾⋅𝐶𝐷=𝐶𝐴⋅𝐶𝐵
(hằng số).
Tâm đường tròn ngoại tiếp △AKDtriangle cap A cap K cap D
△𝐴𝐾𝐷
có tính chất gì?
Gọi Hcap H
𝐻
là trực tâm △ABDtriangle cap A cap B cap D
△𝐴𝐵𝐷
. Kcap K
𝐾
chính là Hcap H
𝐻
.
O′cap O prime
𝑂′
là tâm đường tròn ngoại tiếp △AKDtriangle cap A cap K cap D
△𝐴𝐾𝐷
.
O′cap O prime
𝑂′
nằm trên đường trung trực của ADcap A cap D
𝐴𝐷
.
O′cap O prime
𝑂′
nằm trên đường trung trực của AKcap A cap K
𝐴𝐾
.
Khi Kcap K
𝐾
di động, O′cap O prime
𝑂′
di động.
Ta có ∠AKD=90∘angle cap A cap K cap D equals 90 raised to the composed with power
∠𝐴𝐾𝐷=90∘
(không đúng, ∠BKD=90∘angle cap B cap K cap D equals 90 raised to the composed with power
∠𝐵𝐾𝐷=90∘
).
∠CAD=∠CBDangle cap C cap A cap D equals angle cap C cap B cap D
∠𝐶𝐴𝐷=∠𝐶𝐵𝐷
(không đúng).
∠KAD=∠KBDangle cap K cap A cap D equals angle cap K cap B cap D
∠𝐾𝐴𝐷=∠𝐾𝐵𝐷
(không đúng).
∠ADK=∠ABKangle cap A cap D cap K equals angle cap A cap B cap K
∠𝐴𝐷𝐾=∠𝐴𝐵𝐾
(không đúng).
Tâm O′cap O prime
𝑂′
của đường tròn ngoại tiếp △AKDtriangle cap A cap K cap D
△𝐴𝐾𝐷
có bán kính R=AD2sin(∠AKD)cap R equals the fraction with numerator cap A cap D and denominator 2 sine open paren angle cap A cap K cap D close paren end-fraction
𝑅=𝐴𝐷2sin(∠𝐴𝐾𝐷)
.
Ta biết ∠ACD=90∘angle cap A cap C cap D equals 90 raised to the composed with power
∠𝐴𝐶𝐷=90∘
. Tứ giác ACMDcap A cap C cap M cap D
𝐴𝐶𝑀𝐷
nội tiếp đường tròn đường kính ADcap A cap D
𝐴𝐷
.
Tâm đường tròn ngoại tiếp △AKDtriangle cap A cap K cap D
△𝐴𝐾𝐷
là trung điểm của ADcap A cap D
𝐴𝐷
(không đúng, chỉ đúng nếu Kcap K
𝐾
nằm trên đường tròn đó).
△AKDtriangle cap A cap K cap D
△𝐴𝐾𝐷
không nhất thiết là tam giác vuông.
∠ACD=90∘angle cap A cap C cap D equals 90 raised to the composed with power
∠𝐴𝐶𝐷=90∘
. Tứ giác ACMDcap A cap C cap M cap D
𝐴𝐶𝑀𝐷
nội tiếp đường tròn đường kính ADcap A cap D
𝐴𝐷
.
Tâm của đường tròn ngoại tiếp tứ giác ACMDcap A cap C cap M cap D
𝐴𝐶𝑀𝐷
là trung điểm O′cap O prime
𝑂′
của ADcap A cap D
𝐴𝐷
.
O′cap O prime
𝑂′
là trung điểm của ADcap A cap D
𝐴𝐷
.
Khi Kcap K
𝐾
di động, Dcap D
𝐷
di động, Acap A
𝐴
cố định. O′cap O prime
𝑂′
di động trên đường nào?
Ccap C
𝐶
cố định. CA⋅CB=CK⋅CDcap C cap A center dot cap C cap B equals cap C cap K center dot cap C cap D
𝐶𝐴⋅𝐶𝐵=𝐶𝐾⋅𝐶𝐷
.
CBcap C cap B
𝐶𝐵
cố định. CAcap C cap A
𝐶𝐴
cố định. CA⋅CBcap C cap A center dot cap C cap B
𝐶𝐴⋅𝐶𝐵
là hằng số. CK⋅CDcap C cap K center dot cap C cap D
𝐶𝐾⋅𝐶𝐷
là hằng số.
Kcap K
𝐾
di động trên CIcap C cap I
𝐶𝐼
. Dcap D
𝐷
di động trên tia CIcap C cap I
𝐶𝐼
.
CD=CA⋅CBCKcap C cap D equals the fraction with numerator cap C cap A center dot cap C cap B and denominator cap C cap K end-fraction
𝐶𝐷=𝐶𝐴⋅𝐶𝐵𝐶𝐾
Kcap K
𝐾
nằm giữa Ccap C
𝐶
và Icap I
𝐼
.
Dcap D
𝐷
nằm ngoài đoạn CKcap C cap K
𝐶𝐾
.
O′cap O prime
𝑂′
là trung điểm ADcap A cap D
𝐴𝐷
.
Tâm O′cap O prime
𝑂′
nằm trên đường trung trực của ADcap A cap D
𝐴𝐷
.
ACMDcap A cap C cap M cap D
𝐴𝐶𝑀𝐷
nội tiếp.
Gọi O′cap O prime
𝑂′
là tâm đường tròn ngoại tiếp △AKDtriangle cap A cap K cap D
△𝐴𝐾𝐷
.
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠ACDangle cap A cap K cap D equals angle cap A cap C cap D
∠𝐴𝐾𝐷=∠𝐴𝐶𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
∠AKD=∠AMDangle cap A cap K cap D equals angle cap A cap M cap D
∠𝐴𝐾𝐷=∠𝐴𝑀𝐷
(không đúng).
Related links
AI responses may include mistakes. Answers may be inaccurate or misleading. Double-check for accuracy.
Cho nữa đường tròn tâm O đường kính AB. C là một điểm ...
Aug 19, 2025 — Cho nữa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K ...
4.6(902)
Cho nửa đường tròn tâm O đường kính AB, C là một điểm ...
Mar 25, 2021 — Cho nửa đường tròn tâm O đường kính AB, C là một điểm nằm
a. Ta có AB là đường kính của (O)→AM⊥MB
→ CK.CD=CA.CB
c. Ta có K∈(O)→AN⊥NB→BN⊥AD
Vì AM⊥BD, BN⊥AD, AM∩BN={K} → K là trực tâm ΔDAB
→BK⊥AD →B, K, N thẳng hàng
d. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
Ta có CK.CD=CA.CB
→AKDE nội tiếp
→ E∈(AKD)
→ Tâm đường tròn ngoại tiếp ΔAKD nằm trên trung trực AE cố định
Tam giác AMNAMN đồng dạng với tam giác ABCABC, suy ra MN∥BCMN∥BC.
Một định lý quan trọng trong hình học tam giác phát biểu rằng đường thẳng nối tâm ngoại tiếp OO với đỉnh AA luôn vuông góc với đoạn thẳng MNMN nối chân các đường vuông góc từ trực tâm HH xuống hai cạnh kề AA.
Quảng cáo
Bạn hỏi - Chuyên gia trả lời
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
Đã trả lời bởi chuyên gia
70058
-
Đã trả lời bởi chuyên gia
58137
-
Đã trả lời bởi chuyên gia
49380
-
Đã trả lời bởi chuyên gia
48413
-
Đã trả lời bởi chuyên gia
37961
-
Đã trả lời bởi chuyên gia
37471
-
hoa nguyen 135 điểm
-
Kiều Anh
120 điểm
-
iu Uyên /vk iu/ >.<
95 điểm
-
omaichuoi
95 điểm
-
౨ৎʏᴜɴɴɪᴇ౨ৎ
85 điểm
-
I miss you
60 điểm
-
Thiên Bình
55 điểm
-
ngọc linh 50 điểm
-
axt.
35 điểm
-
Phương Anna Phạm 35 điểm
-
`d.`
25 điểm
Rút gọn
Bài viết mới nhất Lớp 9
-
4 năm trước6907
-
4 năm trước6265
-
4 năm trước5732
-
4 năm trước5733
