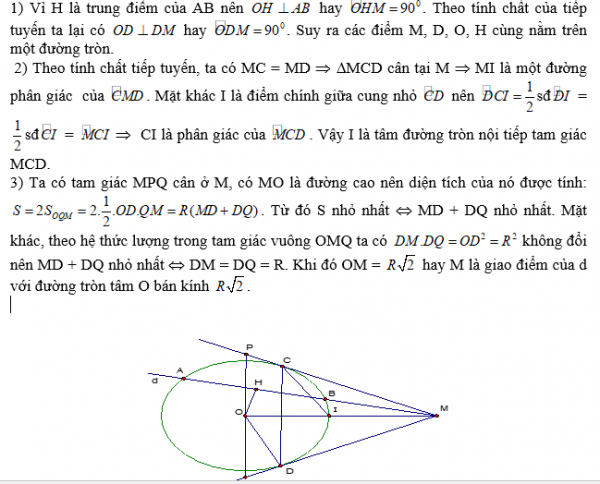
Cho đường trong (O, R) và đường thẳng d không qua O cắt đường tròn tại hai điểm A, B. Lấy một điểm M trên tia đối của tia BA kẻ hai tiếp tuyến MC, MD với đường tròn (C, D là các tiếp điểm). Gọi H là trung điểm của AB.
1) Chứng minh rằng các điểm M, D, O, H cùng nằm trên một đường tròn.
2) Đoạn OM cắt đường tròn tại I. Chứng minh rằng I là tâm đường tròn nội tiếp tam giác MCD.
3) Đường thẳng qua O, vuông góc với OM cắt các tia MC, MD thứ tự tại P và Q. Tìm vị trí của điểm M trên d sao cho diện tích tam giác MPQ bé nhất.
Quảng cáo
6 câu trả lời 57597
Cho đường trong (O, R) và đường thẳng d không qua O cắt đường tròn tại hai điểm A, B. Lấy một điểm M trên tia đối của tia BA kẻ hai tiếp tuyến MC, MD với đường tròn (C, D là các tiếp điểm). Gọi H là trung điểm của AB.
1) Chứng minh rằng các điểm M, D, O, H cùng nằm trên một đường tròn.
2) Đoạn OM cắt đường tròn tại I. Chứng minh rằng I là tâm đường tròn nội tiếp tam giác MCD.
3) Đường thẳng qua O, vuông góc với OM cắt các tia MC, MD thứ tự tại P và Q. Tìm vị trí của điểm M trên d sao cho diện tích tam giác MPQ bé nhất.
a) zì H là trung điểm của AB nên ��⊥��OH⊥ABhay ���^=900OHM=900
theo tính chất của tiếp tuyến ta lại có ��⊥��(ℎ��)���^=900OD⊥DM(hay)ODM=900
=> M,D,O,H cùng nằm trên 1đường tròn
b) Theo tính chất tiếp tuyến ta có
MC=MD=> tam giác MDC cân tại M
=> MI là 1 đương phân giác của CMD , MẶt khác I là điểm chính giữa cung nhỏ CD nên :
���^=12�đ\widebat��=12�đ\widebat��=���^DCI=21sđ\widebatDI=21sđ\widebatCI=MCI
=> CI là phân giác của góc MCD .
zậy I là tâm đường tròn nội tiếp tam giác MCD
Cho đường trong (O, R) và đường thẳng d không qua O cắt đường tròn tại hai điểm A, B. Lấy một điểm M trên tia đối của tia BA kẻ hai tiếp tuyến MC, MD với đường tròn (C, D là các tiếp điểm). Gọi H là trung điểm của AB.
1) Chứng minh rằng các điểm M, D, O, H cùng nằm trên một đường tròn.
2) Đoạn OM cắt đường tròn tại I. Chứng minh rằng I là tâm đường tròn nội tiếp tam giác MCD.
3) Đường thẳng qua O, vuông góc với OM cắt các tia MC, MD thứ tự tại P và Q. Tìm vị trí của điểm M trên d sao cho diện tích tam giác MPQ bé nhất.
Step 1: Chứng minh tứ giác MDOH nội tiếp
Theo tính chất hai tiếp tuyến cắt nhau, ta có ∠ODM=90∘angle cap O cap D cap M equals 90 raised to the composed with power
∠𝑂𝐷𝑀=90∘
.
Vì H là trung điểm của AB, nên OH⟂ABcap O cap H ⟂ cap A cap B
𝑂𝐻⟂𝐴𝐵
hay ∠OHM=90∘angle cap O cap H cap M equals 90 raised to the composed with power
∠𝑂𝐻𝑀=90∘
.
Tứ giác MDOH có ∠ODM+∠OHM=90∘+90∘=180∘angle cap O cap D cap M plus angle cap O cap H cap M equals 90 raised to the composed with power plus 90 raised to the composed with power equals 180 raised to the composed with power
∠𝑂𝐷𝑀+∠𝑂𝐻𝑀=90∘+90∘=180∘
.
Do đó, tứ giác MDOH nội tiếp một đường tròn.
Answer:
Các điểm M, D, O, H cùng nằm trên một đường tròn.
và đường thẳng d - d - không đi qua O - O - cắt đường tròn
Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt đường tròn. ... Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt ...
R ) và đường thẳng d không đi qua O cắt đường tròn tại hai ...
Mar 3, 2025 — * ĐHQG Hồ Chí Minh. 328 đề thi. * ĐH Bách Khoa. 342 đề thi. * ĐHQG Hà Nội. 361 đề thi. * Bộ Công an. 3 đề thi. * ĐHSP ...
2. Chứng minh I là tâm đường tròn nội tiếp tam giác MCD
Step 1: Chứng minh I thuộc phân giác của ∠CMDangle cap C cap M cap D
∠𝐶𝑀𝐷
Theo tính chất hai tiếp tuyến cắt nhau, OM là tia phân giác của ∠CMDangle cap C cap M cap D
∠𝐶𝑀𝐷
. Vì I nằm trên OM, nên CI là tia phân giác của ∠MCDangle cap M cap C cap D
∠𝑀𝐶𝐷
.
và đường thẳng d - d - không đi qua O - O - cắt đường tròn
Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt đường tròn. ... Cho đường tròn (O;R) và đường thẳng d không đi qua
R ) và đường thẳng d không đi qua O cắt đường tròn tại hai ...
Mar 3, 2025 — * ĐHQG Hồ Chí Minh. 328 đề thi. * ĐH Bách Khoa. 342 đề thi. * ĐHQG Hà Nội. 361 đề thi. * Bộ Công an. 3 đề thi. * ĐHSP ...
Step 2: Chứng minh I thuộc phân giác của ∠MDCangle cap M cap D cap C
∠𝑀𝐷𝐶
Ta có MC=MDcap M cap C equals cap M cap D
𝑀𝐶=𝑀𝐷
(tính chất hai tiếp tuyến cắt nhau), nên △MCDtriangle cap M cap C cap D
△𝑀𝐶𝐷
là tam giác cân tại M.
OM là đường cao, đường trung tuyến, và đường phân giác của △MCDtriangle cap M cap C cap D
△𝑀𝐶𝐷
.
I là giao điểm của phân giác góc M và đường trung trực của CD.
Xét đường tròn (O), ta có OC=OD=Rcap O cap C equals cap O cap D equals cap R
𝑂𝐶=𝑂𝐷=𝑅
.
Xét đường tròn đi qua M, D, O, H (đường tròn ngoại tiếp tứ giác MDOH), ta có MD=MCcap M cap D equals cap M cap C
𝑀𝐷=𝑀𝐶
.
Trong △ODCtriangle cap O cap D cap C
△𝑂𝐷𝐶
, OD=OCcap O cap D equals cap O cap C
𝑂𝐷=𝑂𝐶
, nên △ODCtriangle cap O cap D cap C
△𝑂𝐷𝐶
cân tại O.
∠IDC=∠IMCangle cap I cap D cap C equals angle cap I cap M cap C
∠𝐼𝐷𝐶=∠𝐼𝑀𝐶
(góc nội tiếp cùng chắn cung IC trong đường tròn ngoại tiếp tứ giác MDOH).
∠ICD=∠IDMangle cap I cap C cap D equals angle cap I cap D cap M
∠𝐼𝐶𝐷=∠𝐼𝐷𝑀
(OM là phân giác của ∠CMDangle cap C cap M cap D
∠𝐶𝑀𝐷
).
Do đó, I là giao điểm của các đường phân giác trong của △MCDtriangle cap M cap C cap D
△𝑀𝐶𝐷
.
và đường thẳng d - d - không đi qua O - O - cắt đường tròn
Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt đường tròn. ... Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt ...
R ) và đường thẳng d không đi qua O cắt đường tròn tại hai ...
Mar 3, 2025 — * ĐHQG Hồ Chí Minh. 328 đề thi. * ĐH Bách Khoa. 342 đề thi. * ĐHQG Hà Nội. 361 đề thi. * Bộ Công an. 3 đề thi. * ĐHQG
Answer:
I là tâm đường tròn nội tiếp tam giác MCD.
và đường thẳng d - d - không đi qua O - O - cắt đường tròn
Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt đường tròn. ... Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt ...
R ) và đường thẳng d không đi qua O cắt đường tròn tại hai ...
Mar 3, 2025 — * ĐHQG Hồ Chí Minh. 328 đề thi. * ĐH Bách Khoa. 342 đề thi. * ĐHQG Hà Nội. 361 đề thi. * Bộ Công an. 3 đề thi. * ĐHSP ...
3. Tìm vị trí của điểm M trên d sao cho diện tích tam giác MPQ bé nhất
Step 1: Thiết lập biểu thức diện tích tam giác MPQ
Gọi R là bán kính đường tròn (O). OM cắt CD tại K. OM⟂CDcap O cap M ⟂ cap C cap D
𝑂𝑀⟂𝐶𝐷
tại K.
Ta có MC=R⋅cot(∠CMD2)cap M cap C equals cap R center dot cotangent open paren the fraction with numerator angle cap C cap M cap D and denominator 2 end-fraction close paren
𝑀𝐶=𝑅⋅cot(∠𝐶𝑀𝐷2)
.
△MPQtriangle cap M cap P cap Q
△𝑀𝑃𝑄
vuông tại O. OK là đường cao.
△MOPtriangle cap M cap O cap P
△𝑀𝑂𝑃
vuông tại O. OK là đường cao. MC2=MK⋅MOcap M cap C squared equals cap M cap K center dot cap M cap O
𝑀𝐶2=𝑀𝐾⋅𝑀𝑂
.
Ta có MC=MDcap M cap C equals cap M cap D
𝑀𝐶=𝑀𝐷
. △MCDtriangle cap M cap C cap D
△𝑀𝐶𝐷
cân tại M.
△MPQtriangle cap M cap P cap Q
△𝑀𝑃𝑄
vuông tại O.
và đường thẳng d - d - không đi qua O - O - cắt đường tròn
Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt đường tròn. ... Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt ...
R ) và đường thẳng d không đi qua O cắt đường tròn tại hai ...
Mar 3, 2025 — * ĐHQG Hồ Chí Minh. 328 đề thi. * ĐH Bách Khoa. 342 đề thi. * ĐHQG Hà Nội. 361 đề thi. * Bộ Công an. 3 đề thi. * ĐHSP ...
SMPQ=12⋅OP⋅OQcap S sub cap M cap P cap Q end-sub equals one-half center dot cap O cap P center dot cap O cap Q
𝑆𝑀𝑃𝑄=12⋅𝑂𝑃⋅𝑂𝑄
và đường thẳng d - d - không đi qua O - O - cắt đường tròn
Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt đường tròn. ... Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt ...
R ) và đường thẳng d không đi qua O cắt đường tròn tại hai ...
Mar 3, 2025 — * ĐHQG Hồ Chí Minh. 328 đề thi. * ĐH Bách Khoa. 342 đề thi. * ĐHQG Hà Nội. 361 đề thi. * Bộ Công an. 3 đề thi. * ĐHSP ...
△MCO∼△OCPtriangle cap M cap C cap O tilde triangle cap O cap C cap P
△𝑀𝐶𝑂∼△𝑂𝐶𝑃
(g.g) ⇒MCOC=OCOP⇒OP=OC2MC=R2MCimplies the fraction with numerator cap M cap C and denominator cap O cap C end-fraction equals the fraction with numerator cap O cap C and denominator cap O cap P end-fraction implies cap O cap P equals the fraction with numerator cap O cap C squared and denominator cap M cap C end-fraction equals the fraction with numerator cap R squared and denominator cap M cap C end-fraction
⇒𝑀𝐶𝑂𝐶=𝑂𝐶𝑂𝑃⇒𝑂𝑃=𝑂𝐶2𝑀𝐶=𝑅2𝑀𝐶
.
Tương tự, OQ=R2MD=R2MCcap O cap Q equals the fraction with numerator cap R squared and denominator cap M cap D end-fraction equals the fraction with numerator cap R squared and denominator cap M cap C end-fraction
𝑂𝑄=𝑅2𝑀𝐷=𝑅2𝑀𝐶
.
và đường thẳng d - d - không đi qua O - O - cắt đường tròn
Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt đường tròn. ... Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt ...
R ) và đường thẳng d không đi qua O cắt đường tròn tại hai ...
Mar 3, 2025 — * ĐHQG Hồ Chí Minh. 328 đề thi. * ĐH Bách Khoa. 342 đề thi. * ĐHQG Hà Nội. 361 đề thi. * Bộ Công an. 3 đề thi. * ĐHSP ...
SMPQ=12⋅OP⋅OQ=12⋅R2MC⋅R2MC=R42⋅MC2cap S sub cap M cap P cap Q end-sub equals one-half center dot cap O cap P center dot cap O cap Q equals one-half center dot the fraction with numerator cap R squared and denominator cap M cap C end-fraction center dot the fraction with numerator cap R squared and denominator cap M cap C end-fraction equals the fraction with numerator cap R to the fourth power and denominator 2 center dot cap M cap C squared end-fraction
𝑆𝑀𝑃𝑄=12⋅𝑂𝑃⋅𝑂𝑄=12⋅𝑅2𝑀𝐶⋅𝑅2𝑀𝐶=𝑅42⋅𝑀𝐶2
và đường thẳng d - d - không đi qua O - O - cắt đường tròn
Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt đường tròn. ... Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt ...
R ) và đường thẳng d không đi qua O cắt đường tròn tại hai ...
Mar 3, 2025 — * ĐHQG Hồ Chí Minh. 328 đề thi. * ĐH Bách Khoa. 342 đề thi. * ĐHQG Hà Nội. 361 đề thi. * Bộ Công an. 3 đề thi. * ĐHSP ...
MC2=MO2−OC2=MO2−R2cap M cap C squared equals cap M cap O squared minus cap O cap C squared equals cap M cap O squared minus cap R squared
𝑀𝐶2=𝑀𝑂2−𝑂𝐶2=𝑀𝑂2−𝑅2
SMPQ=R42⋅(MO2−R2)cap S sub cap M cap P cap Q end-sub equals the fraction with numerator cap R to the fourth power and denominator 2 center dot open paren cap M cap O squared minus cap R squared close paren end-fraction
𝑆𝑀𝑃𝑄=𝑅42⋅(𝑀𝑂2−𝑅2)
và đường thẳng d - d - không đi qua O - O - cắt đường tròn
Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt đường tròn. ... Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt ...
R ) và đường thẳng d không đi qua O cắt đường tròn tại hai ...
Mar 3, 2025 — * ĐHQG Hồ Chí Minh. 328 đề thi. * ĐH Bách Khoa. 342 đề thi. * ĐHQG Hà Nội. 361 đề thi. * Bộ Công an. 3 đề thi. * ĐHSP ...
Step 2: Tìm điều kiện để diện tích bé nhất
Diện tích SMPQcap S sub cap M cap P cap Q end-sub
𝑆𝑀𝑃𝑄
bé nhất khi MO2−R2cap M cap O squared minus cap R squared
𝑀𝑂2−𝑅2
lớn nhất, tức là MO lớn nhất.
M nằm trên tia đối của tia BA. H là trung điểm AB. O không thuộc d. OH là khoảng cách từ O đến d.
MO≥OHcap M cap O is greater than or equal to cap O cap H
𝑀𝑂≥𝑂𝐻
(khoảng cách từ O đến điểm trên đường thẳng d).
MO lớn nhất khi M ở vô cực (không có vị trí cụ thể).
Tuy nhiên, nếu M chỉ di chuyển trên đường thẳng d, MO nhỏ nhất khi M trùng với điểm gần O nhất trên d, đó là H. Nhưng M nằm trên tia đối của tia BA.
Giả sử d là đường thẳng chứa AB.
Điểm M nằm trên tia đối của tia BA, tức là M nằm ngoài đoạn AB về phía A.
MO2=OH2+MH2cap M cap O squared equals cap O cap H squared plus cap M cap H squared
𝑀𝑂2=𝑂𝐻2+𝑀𝐻2
. MO lớn nhất khi MH lớn nhất, tức M càng xa H.
Có thể đề bài yêu cầu tìm giá trị nhỏ nhất của diện tích.
SMPQ=R42⋅MC2cap S sub cap M cap P cap Q end-sub equals the fraction with numerator cap R to the fourth power and denominator 2 center dot cap M cap C squared end-fraction
𝑆𝑀𝑃𝑄=𝑅42⋅𝑀𝐶2
. Để SMPQcap S sub cap M cap P cap Q end-sub
𝑆𝑀𝑃𝑄
nhỏ nhất thì MC2cap M cap C squared
𝑀𝐶2
phải lớn nhất, tức MO lớn nhất.
Nếu đề bài yêu cầu tìm giá trị lớn nhất của diện tích, thì SMPQcap S sub cap M cap P cap Q end-sub
𝑆𝑀𝑃𝑄
lớn nhất khi MC2cap M cap C squared
𝑀𝐶2
nhỏ nhất, tức MO nhỏ nhất.
MO nhỏ nhất khi M trùng với H (điểm gần O nhất trên d). Nhưng M nằm trên tia đối của tia BA.
Khoảng cách MO không có giá trị lớn nhất.
và đường thẳng d - d - không đi qua O - O - cắt đường tròn
Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt đường tròn. ... Cho đường tròn (O;R) và đường thẳng d không đi qua O cắt ...
R ) và đường thẳng d không đi qua O cắt đường tròn tại hai ...
Mar 3, 2025 — * ĐHQG Hồ Chí Minh. 328 đề thi. * ĐH Bách Khoa. 342 đề thi. * ĐHQG Hà Nội. 361 đề thi. * Bộ Công an. 3 đề thi. * ĐHSP ...
Answer:
Diện tích tam giác MPQ không có giá trị bé nhất vì MO có thể tăng vô hạn. Có thể đề bài yêu cầu tìm giá trị lớn nhất của diện tích, khi đó M nằm ở vị trí gần H nhất trên tia đối của tia BA.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
104666
Đã trả lời bởi chuyên gia
104666 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69578
Đã trả lời bởi chuyên gia
69578 -
 Đã trả lời bởi chuyên gia
48088
Đã trả lời bởi chuyên gia
48088 -
 Đã trả lời bởi chuyên gia
47019
Đã trả lời bởi chuyên gia
47019 -
 Đã trả lời bởi chuyên gia
37490
Đã trả lời bởi chuyên gia
37490 -
 Đã trả lời bởi chuyên gia
36573
Đã trả lời bởi chuyên gia
36573