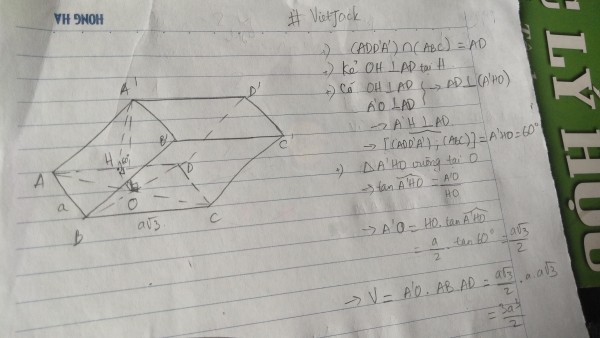Quảng cáo
4 câu trả lời 2429
Gọi $O$ là giao điểm của $AB$ và $BD$
$\Rightarrow A'O\perp (ABCD) \, (gt)$
Gọi $M$ là trung điểm của $AD$
$\Rightarrow OM\perp AD$
Ta có: $A'O$ chung; $OD = OA$ ($ABCD$ là hình chữ nhật)
$\Rightarrow A'A = A'B$
$\Rightarrow ΔA'AB$ cân tại $A'$
$\Rightarrow A'M \perp AD$
Xét hai mặt phẳng $(ADD'A')$ và $(ABCD)$ có:
$\begin{cases}(ADD'A') \cap (ABCD) = AD\\A'M \subset (ADD'A')\\A'M \perp AD \, (cmt)\\OM \subset (ABCD)\\OM \perp AD\end{cases}$
$\\\Rightarrow \widehat{((ADD'A');(ABCD))} = \widehat{A'MO} = 60^o$
$\Rightarrow A'O = OM\sqrt{3}$
mà $OM = \dfrac{1}{2}AB = \dfrac{a}{2}$ (tính chất đường trung bình)
nên $A'O = \dfrac{a\sqrt{3}}{2}$
Ta có: $B'D'//BD$
$\Rightarrow B'D'//(A'BD)$
$\Rightarrow d(B';(A'BD)) = d(B'D';(A'BD)) = d(O';(A'BD))$ $(1)$
Với $O'$ là giao điểm của $A'C'$ và $B'D'$
Mặt khác: $O'C//A'O$
$\Rightarrow O'C//(A'BD)$
$\Rightarrow d(O';(A'BD)) = d(C;(A'BD))$
Từ $C$ kẻ $CH\perp BD$
Ta có: $A'O\perp (ABCD)$
$\Rightarrow A'O\perp CH$
mà $CH\perp BD$ (cách dựng)
nên $CH\perp (A'BD)$
$\Rightarrow CH = d(C;(A'BD))$ $(2)$
$(1)(2) \Rightarrow d(B';(A'BD)) = CH$
Áp dụng định lý Pytago, ta được:
$BD^2 = AB^2 + AD^2 = a^2 + 3a^2 = 4a^2$
$\Rightarrow BD = 2a$
Ta có: $CD.BC = CH.BD = 2S_{BCD}$
$\Rightarrow CH = \dfrac{BC.CD}{BD} = \dfrac{a\sqrt{3}.a}{2a} = \dfrac{a\sqrt{3}}{2}$
Vậy $d(B';(A'BD)) = \dfrac{a\sqrt{3}}{2}$
$S_{ABCD} = AB \cdot AD = a \cdot a\sqrt{3} = a^2\sqrt{3}$
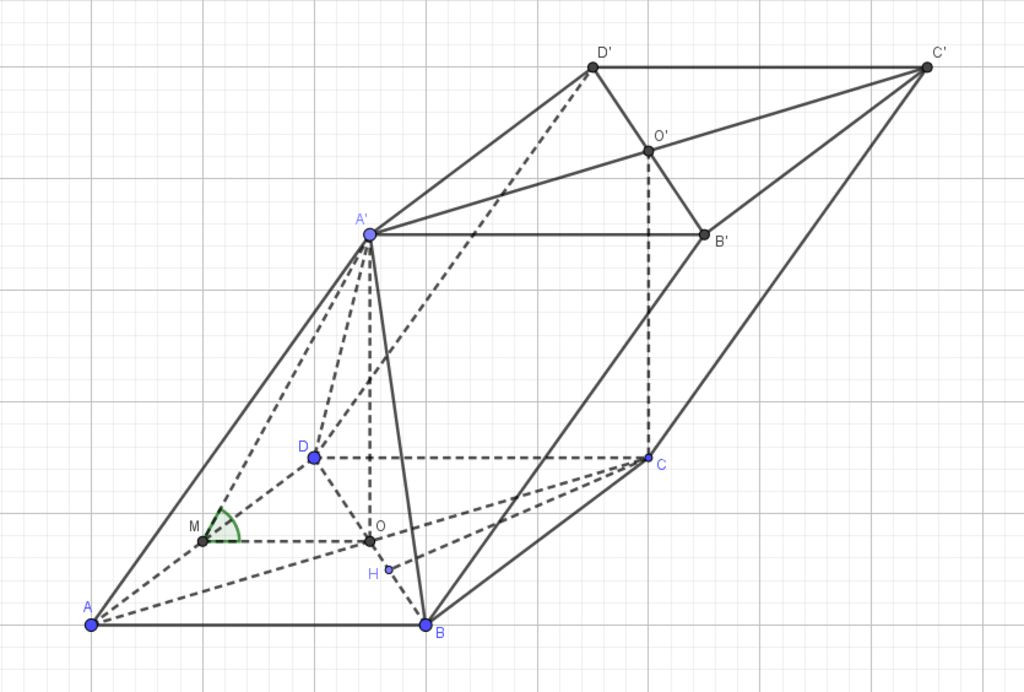
Gọi `O` là giao điểm của `AC` và `BD`. Theo giả thiết, hình chiếu vuông góc của `A'` lên mặt phẳng `(ABCD)` là `O`, do đó $A'O \perp (ABCD)$. Chiều cao của lăng trụ là $h = A'O$.
Góc giữa hai mặt phẳng `(ADD'A')` và `(ABCD)` được xác định như sau:
Giao tuyến của hai mặt phẳng là đường thẳng `AD`.
Trong mặt phẳng `(ABCD)`, kẻ $OM \perp AD$ tại `M`. Vì `ABCD` là hình chữ nhật và `O` là tâm, `M` là trung điểm của `AD` và `OM` song song với `AB`. Do đó, $OM = \frac{AB}{2} = \frac{a}{2}$.
Vì $A'O \perp (ABCD)$ và $OM \perp AD$, theo định lý ba đường vuông góc, ta có $A'M \perp AD$.
Góc giữa hai mặt phẳng `(ADD'A')` và `(ABCD)` là góc giữa hai đường thẳng `OM` và `A'M`, chính là góc $\widehat{A'MO} = 60^\circ$.
* Xét tam giác `A'OM` vuông tại `O`, ta có:
$\tan(\widehat{A'MO}) = \frac{A'O}{OM}$
$\Rightarrow A'O = OM \cdot \tan(60^\circ) = \frac{a}{2} \cdot \sqrt{3} = \frac{a\sqrt{3}}{2}$
Vậy, chiều cao của lăng trụ là $h = \frac{a\sqrt{3}}{2}$.
Thể tích của khối lăng trụ là:
$V = S_{ABCD} \cdot h = (a^2\sqrt{3}) \cdot \left(\frac{a\sqrt{3}}{2}\right) = \frac{3a^3}{2}$
SABCD=AB⋅AD=a⋅a√3=a2√3
Gọi O là giao điểm của AC và BD. Theo giả thiết, hình chiếu vuông góc của A' lên mặt phẳng (ABCD) là O, do đó A′O⊥(ABCD). Chiều cao của lăng trụ là h=A′O.
Góc giữa hai mặt phẳng (ADD'A') và (ABCD) được xác định như sau:
Giao tuyến của hai mặt phẳng là đường thẳng AD.
Trong mặt phẳng (ABCD), kẻ OM⊥AD tại M. Vì ABCD là hình chữ nhật và O là tâm, M là trung điểm của AD và OM song song với AB. Do đó, OM=AB2=a2.
Vì A′O⊥(ABCD) và OM⊥AD, theo định lý ba đường vuông góc, ta có A′M⊥AD.
Góc giữa hai mặt phẳng (ADD'A') và (ABCD) là góc giữa hai đường thẳng OM và A'M, chính là góc ˆA′MO=60∘.
* Xét tam giác A'OM vuông tại O, ta có:
tan(ˆA′MO)=A′OOM
⇒A′O=OM⋅tan(60∘)=a2⋅√3=a√32
Vậy, chiều cao của lăng trụ là h=a√32.
Thể tích của khối lăng trụ là:
V=SABCD⋅h=(a2√3)⋅(a√32)=3a32
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129857
Đã trả lời bởi chuyên gia
129857 -
 Đã trả lời bởi chuyên gia
104336
Đã trả lời bởi chuyên gia
104336 -
 Đã trả lời bởi chuyên gia
94255
Đã trả lời bởi chuyên gia
94255 -
 Đã trả lời bởi chuyên gia
70288
Đã trả lời bởi chuyên gia
70288