VuNguyen✓★
Kim cương đoàn
12,415
2483
Câu hỏi:
Câu trả lời của bạn: 08:20 22/04/2025
x-∞-226+∞\hlinex-6-|-|-0+(x+2)5-0+|+|+x-2-|-0+|+\hlinef'(x)-0+0-0+Biến thiên f(x)↘↗↘↗Cực tiểuCực đạiCực tiểu
Câu trả lời của bạn: 08:57 06/04/2025
Hàm số
y=(3−2m)x2 (với m≠32) đồng biến với mọi x>0
⇔ Hệ số a=3−2m>0
⇔3>2m
⇔m<32
0<m<32
Vậy, hàm số đồng biến với mọi x>0 khi 0<m<32.
Câu trả lời của bạn: 16:22 05/04/2025
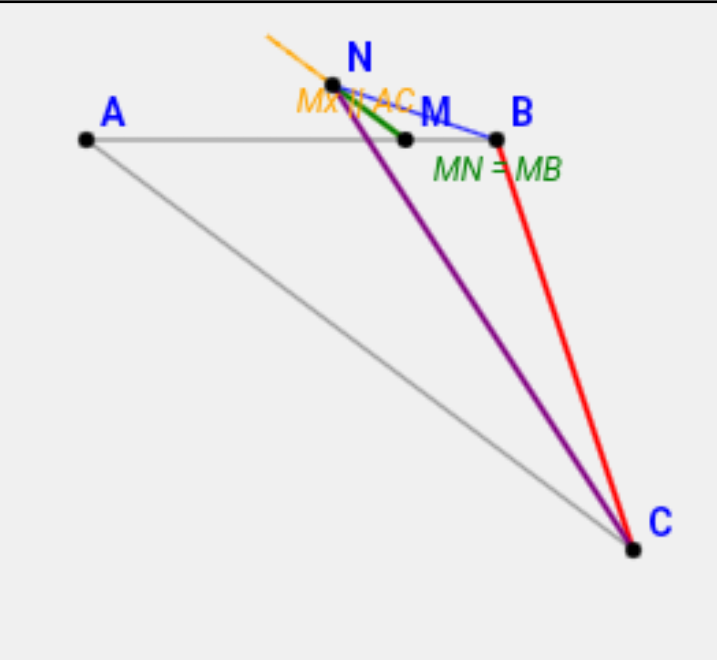
1.
Xét △MBN ta có :
MN=MB (gt - giả thiết).
Suy ra △MBN cân tại M.
Do đó, ^BNM=^NBM (góc ở đáy).
2.
Tia Mx nằm trên nửa mặt phẳng bờ AB không chứa C.
Do đó, N và C nằm khác phía đối với đường thẳng AB.
Vì M∈AB, tia BM và tia BA trùng nhau.
Suy ra, tia BN nằm giữa hai tia BA và BC.
Do đó, ^ABC+^NBM=^NBC.
3.
Ta có: ^NBC=^ABC+^NBM.
Mà ^NBM=^BNM (Cmt ).
Suy ra: ^NBC=^ABC+^BNM.
Góc ^BNC chính là góc ^BNM.
Vì ^ABC>0∘ (do A,B,C là 3 đỉnh tam giác), nên ^ABC+^BNM>^BNM.
Vậy, ^NBC>^BNC.
Câu trả lời của bạn: 16:14 05/04/2025
a)
Δ′=[−(m−1)]2−1⋅(m2−3)
Δ′=(m−1)2−(m2−3)
Δ′=m2−2m+1−m2+3
Δ′=−2m+4
Δ′≥0
⇔−2m+4≥0
⇔−2m≥−4
⇔m≤2
Vậy m≤2 thì phương trình có nghiệm.
b)
Δ′>0⇔−2m+4>0⇔m<2.
Gọi x1,x2 là hai nghiệm của phương trình.
{x1+x2=2(m−1)(1)x1x2=m2−3(2)
3x2+x2=2(m−1)
⇔4x2=2(m−1)
⇔x2=m−12
x1=3x2=3(m−1)2
3(m−1)2⋅m−12=m2−3
⇔3(m−1)24=m2−3
⇔3(m2−2m+1)=4(m2−3)
⇔3m2−6m+3=4m2−12
⇔m2+6m−15=0
Δm=62−4⋅1⋅(−15)=36+60=96
√Δm=√96=4√6
m=−6±4√62=−3±2√6
Kiểm tra điều kiện m<2:
m=−3+2√6≈−3+2(2.45)=−3+4.9=1.9<2 (Thỏa mãn)
m=−3−2√6<0<2 (Thỏa mãn)
Vậy m=−3±2√6
Câu hỏi:
Câu trả lời của bạn: 16:11 05/04/2025
x2≥0 với mọi x
|2x−1|≥0 với mọi x
⇒x2+|2x−1|≥0 với mọi x.
Do đó,
|x2+|2x−1||=x2+|2x−1|.
x2+|2x−1|=x2+3
⇒|2x−1|=(x2+3)−x2
⇒|2x−1|=3
Xét 2 TH
Th 1: 2x−1=3
⇒2x=3+1
⇒2x=4
⇒x=4÷2
⇒x=2
Th2: 2x−1=−3
⇒2x=−3+1
⇒2x=−2
⇒x=−2÷2
⇒x=−1
Vậy x∈{2;−1}.
Câu trả lời của bạn: 22:34 03/04/2025
Gọi x (ngày) là thời gian người thợ thứ nhất làm một mình xong công việc (x>6).
Gọi y (ngày) là thời gian người thợ thứ hai làm một mình xong công việc (y>6).
Trong 1 ngày, người thứ nhất làm được 1x công việc.
Trong 1 ngày, người thứ hai làm được 1y công việc.
Trong 1 ngày, cả hai người làm được 16 công việc.
ta có phương trình:
1x+1y=16 (1)
ta có phương trình:
5x+4y=79 (2)
Đặt u=1x và v=1y (với u>0,v>0). Hệ phương trình trở thành:
{u+v=165u+4v=79
5u+4(16−u)=79
5u+23−4u=79
u=79−23=79−69=19
Suy ra v=16−19=318−218=118
u=19⟹1x=19⟹x=9 (thỏa mãn điều kiện x>6)
v=118⟹1y=118⟹y=18 (thỏa mãn điều kiện y>6)
Câu trả lời của bạn: 10:44 02/04/2025
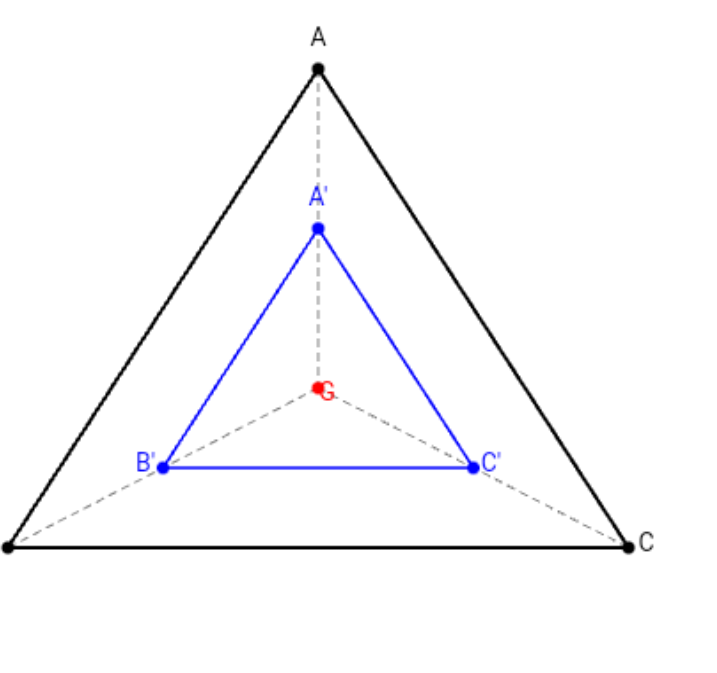
Xét △ABG:
A′ là trung điểm AG (giả thiết)
B′ là trung điểm BG (giả thiết)
⟹A′B′ là đường trung bình của △ABG.
⟹A′B′=12AB (Tính chất đường trung bình) (1)
Xét △BCG:
B′ là trung điểm BG (giả thiết)
C′ là trung điểm CG (giả thiết)
⟹B′C′ là đường trung bình của △BCG.
⟹B′C′=12BC (Tính chất đường trung bình) (2)
Xét △CAG:
C′ là trung điểm CG (giả thiết)
A′ là trung điểm AG (giả thiết)
⟹C′A′ là đường trung bình của △CAG.
⟹C′A′=12CA (Tính chất đường trung bình) (3)
Từ (1), (2) và (3) suy ra:
A′B′AB=B′C′BC=C′A′CA=12
Xét △A′B′C′ và △ABC có:
A′B′AB=B′C′BC=C′A′CA
Vậy △A′B′C′∼△ABC (trường hợp cạnh - cạnh - cạnh).
Câu trả lời của bạn: 08:34 31/03/2025
Yếu tố chính: Độ bền liên kết H-X (Năng lượng liên kết).
Xu hướng: Đi từ F đến I:
Bán kính nguyên tử Halogen (X) tăng: RF<RCl<RBr<RI.
Độ dài liên kết H-X tăng.
Năng lượng liên kết H-X giảm: EH−F>EH−Cl>EH−Br>EH−I.
Kết luận:
Liên kết H-X càng yếu (năng lượng liên kết càng thấp), càng dễ phân ly ra ion H+ trong dung dịch.
Do đó, tính acid tăng dần: HF≪HCl<HBr<HI.
HF: Liên kết H-F rất bền ⟹ khó phân ly H+ ⟹ acid yếu.
HCl,HBr,HI: Liên kết kém bền hơn đáng kể, dễ phân ly H+ hoàn toàn ⟹ acid mạnh. Độ mạnh tăng do năng lượng liên kết giảm dần.
Phương trình phân ly (minh họa):
Acid yếu: HF⇌H++F−
Acid mạnh: HX⟶H++X− (với X=Cl,Br,I)
Câu trả lời của bạn: 08:30 31/03/2025
Câu 1:
a) Đúng. Hàm số đồng biến trên (−∞;−1) ( y′>0 ).
b) Đúng. Hàm số nghịch biến trên (−1;1) ( y′<0 ).
c) Sai. Hàm số đồng biến trên (1;+∞) ( y′>0 ).
d) Sai. Hàm số không đồng biến trên (0;+∞) (nghịch biến trên (0;1) và đồng biến trên (1;+∞)).
Câu 2:
a) Đúng. y′ đổi dấu từ + sang − tại x=1.
b) Sai. Hàm số chỉ có một điểm cực đại tại x=1.
c) Sai. Hàm số có hai điểm cực trị là x=−1 (cực tiểu) và x=1 (cực đại).
d) Đúng. y′ đổi dấu từ − sang + tại x=−1.
Câu 3:
a) Đúng. Điểm cực đại của đồ thị hàm số là (−1;2).
b) Đúng. Điểm cực tiểu của đồ thị hàm số là (1;−2).
c) Sai. (2;−1) không phải điểm cực trị.
d) Sai. (1;−2) là điểm cực tiểu.
Câu 4:
a) Đúng. Đồ thị đi lên trên khoảng (−∞;0).
b) Đúng. Đồ thị đi xuống trên khoảng (0;2).
c) Sai. Hàm số nghịch biến trên (0;2) và đồng biến trên (2;+∞).
d) Sai. Đồ thị đi lên trên khoảng (2;+∞), hàm số đồng biến.
Câu 5:
a) Đúng. Hàm số đạt cực tiểu tại x=2.
b) Đúng. Giá trị cực đại của hàm số là yCĐ=2 (tại x=−2).
c) Sai. Điểm (−2;2) là điểm cực đại của đồ thị hàm số.
d) Đúng. Hàm số đạt cực đại tại x=−2.
Câu 6: Cho hàm số y=ax3+bx2+cx+d (a≠0).
a) Đúng. Đồ thị hàm bậc ba luôn có tâm đối xứng là điểm uốn I(x0,y0) với x0=−b3a.
b) Đúng. limx→±∞y=±∞ (hoặc ∓∞), hàm số liên tục nên đồ thị cắt trục hoành ít nhất 1 lần.
c) Sai. Hàm số có cực trị khi y′=3ax2+2bx+c=0 có 2 nghiệm phân biệt, tức là Δ′=b2−3ac>0. Nếu b2−3ac≤0 thì hàm số không có cực trị. Ví dụ: y=x3.
d) Sai. limx→+∞y=+∞ nếu a>0 và limx→+∞y=−∞ nếu a<0. Chưa đủ thông tin về a.
Câu 7: (Phân tích dựa trên đồ thị được cung cấp)
a) Sai. Đồ thị có tiệm cận đứng là x=1. Do a≠1 (theo đề bài), nên TCĐ không phải x=a.
b) Sai. Đồ thị có tiệm cận ngang là y=2.
c) Đúng. Đồ thị có tiệm cận đứng là x=1.
d) Đúng. Đồ thị có tiệm cận ngang là y=2.
(Lưu ý: Có sự mâu thuẫn giữa dạng hàm số y=x+1x−a,a≠1 (có TCĐ x=a, TCN y=1) và đồ thị được cho (có TCĐ x=1, TCN y=2). Đáp án dựa trên thông tin từ đồ thị.)
Câu 8: Cho hàm số y=x4−2x2+1.
Xét phương trình hoành độ giao điểm: x4−2x2+1=0.
Đặt t=x2 (t≥0). Phương trình trở thành t2−2t+1=0⇔(t−1)2=0⇔t=1.
Với t=1⇒x2=1⇔x=±1.
Phương trình có 2 nghiệm phân biệt.
a) Sai.
b) Đúng. Đồ thị cắt trục hoành tại 2 điểm phân biệt là x=1 và x=−1.
c) Sai.
d) Sai.
Câu trả lời của bạn: 08:26 31/03/2025
`python
import math
# --- Hàm kiểm tra số nguyên tố ---
# Định nghĩa: p là số nguyên tố nếu p > 1 và p chỉ có hai ước số dương là 1 và chính nó.
# LaTeX: p∈P⟺(p>1)∧(∀d∈Z+,d|p⟹d=1∨d=p)
def la_so_nguyen_to(num):
if num < 2:
return False
# Chỉ cần kiểm tra ước đến căn bậc hai của num
# LaTeX: ∀i∈[2,⌊√num⌋]
for i in range(2, int(math.sqrt(num)) + 1):
# Nếu num chia hết cho i (num % i == 0) thì không phải số nguyên tố
# LaTeX: num \pmod{i} == 0
if num % i == 0:
return False
return True
# --- Hàm kiểm tra số hoàn hảo ---
# Định nghĩa: n là số hoàn hảo nếu n > 0 và tổng các ước số dương thực sự của nó (không kể n) bằng chính n.
# LaTeX: n \text{ là số hoàn hảo} \iff (n > 0) \land (\sum_{d|n, d<n} d = n)
def la_so_hoan_hao(num):
if num < 2: # Số hoàn hảo nhỏ nhất là 6
return False
tong_uoc = 0
# Duyệt các số từ 1 đến num-1 để tìm ước
for i in range(1, num):
if num % i == 0:
tong_uoc += i
# So sánh tổng ước với chính số đó
return tong_uoc == num
# --- Chương trình chính ---
# 1. Nhập n
n = int(input("Nhập số nguyên dương n (n>=2): "))
# 2. Tạo danh sách a từ 2 đến n
# LaTeX: a = [2, 3, ..., n]
a = list(range(2, n + 1))
# 3. Khởi tạo biến đếm
dem_so_nguyen_to = 0
dem_so_hoan_hao = 0
# 4. Duyệt danh sách a và đếm
# LaTeX: \forall x \in a
for so in a:
if la_so_nguyen_to(so):
dem_so_nguyen_to += 1
if la_so_hoan_hao(so):
dem_so_hoan_hao += 1
# 5. In kết quả
# print(f"Danh sách a: {a}") # Bỏ dòng này để ngắn gọn
print(f"Số lượng số nguyên tố: {dem_so_nguyen_to}")
print(f"Số lượng số hoàn hảo: {dem_so_hoan_hao}")
`
Trọng tâm bài làm:
1. Nhập n: Lấy giá trị n từ người dùng.
2. Tạo danh sách a: Sử dụng range(2, n + 1) để tạo dãy số và chuyển thành danh sách. a = [2, 3, ..., n].
3. Hàm la_so_nguyen_to(num):
Kiểm tra num < 2 trả về False.
Duyệt i từ 2 đến \lfloor\sqrt{num}\rfloor.
Nếu num % i == 0, trả về False.
Nếu hết vòng lặp, trả về True.
4. Hàm la_so_hoan_hao(num):
Kiểm tra num < 2 trả về False.
Tính tổng các ước d của num sao cho 1 \le d < num. Kí hiệu tổng: S = \sum_{d|num, d<num} d.
Trả về True nếu S = num, ngược lại False.
5. Duyệt và đếm: Dùng vòng lặp for duyệt qua từng so trong danh sách a. Gọi các hàm kiểm tra và tăng biến đếm tương ứng.
6. In kết quả: Hiển thị hai giá trị đếm được.
Câu hỏi:
Câu trả lời của bạn: 08:23 31/03/2025
CH_3-C \equiv CH + AgNO_3 + NH_3 \rightarrow CH_3-C \equiv CAg \downarrow + NH_4NO_3
Số mol propyne:
n_{C_3H_4} = \frac{V}{22.4} = \frac{4.958}{22.4} \approx 0.2213 \text{ (mol)}
Số mol kết tủa:
Theo phương trình, n_{CH_3-C \equiv CAg} = n_{C_3H_4}
\Rightarrow n_{\downarrow} = 0.2213 \text{ (mol)}
Khối lượng kết tủa:
M_{CH_3-C \equiv CAg} = 12 \times 3 + 1 \times 3 + 108 = 147 \text{ (g/mol)}
m_{\downarrow} = n_{\downarrow} \times M_{CH_3-C \equiv CAg} = 0.2213 \times 147 \approx 32.54 \text{ (g)}
=>Vậy khối lượng kết tủa thu được là 32.54 gam.
Câu trả lời của bạn: 08:20 31/03/2025
Tóm tắt:
Khối lượng đạn: m_đ = 10 \text{ g} = 0.01 \text{ kg}
Khối lượng súng: m_s = 5 \text{ kg}
Vận tốc đạn (sau khi bắn): v_đ = 600 \text{ m/s}
Vận tốc súng (giật lùi): v_s = ?
---------
\vec{P}_{\text{trước}} = \vec{P}_{\text{sau}}
Vì ban đầu hệ đứng yên nên \vec{P}_{\text{trước}} = \vec{0}.
\vec{0} = m_đ \vec{v}_đ + m_s \vec{v}_s
0 = m_đ v_đ + m_s v_s
0 = (0.01 \text{ kg}) * (600 \text{ m/s}) + (5 \text{ kg}) * v_s
0 = 6 + 5 v_s
5 v_s = -6
v_s = -\frac{6}{5} = -1.2 \text{ m/s}
=>Vận tốc giật của súng là v_s = -1.2 \text{ m/s}. Dấu "-" cho biết súng giật lùi ngược chiều đạn bay. Độ lớn vận tốc giật là 1.2 \text{ m/s}.
Câu hỏi:
Câu trả lời của bạn: 20:52 30/03/2025
12x² + 7x + 4
____________________
x - 1 | 12x³ - 5x² - 3x - 4
- (12x³ - 12x²)
____________________
7x² - 3x
- (7x² - 7x)
____________________
4x - 4
- (4x - 4)
___________
0
Hoặc
(12x^3 - 5x^2 - 3x - 4) : (x - 1)
= 12x^2 + 7x + 4
Câu hỏi:
Câu trả lời của bạn: 17:29 18/03/2025
Đoạn dây đồng dài
l = 4m
tiết diện
S = 5mm^2 = 5.10^{-6}m^2. Điện trở suất
\rho = 1,7.10^{-8}\Omega m.
Điện trở của dây là :
R = \rho \frac{l}{S}
R = 1,7.10^{-8} \frac{4}{5.10^{-6}} = 0,0136 \Omega
Câu trả lời của bạn: 17:25 18/03/2025
Zn + H_2SO_4 \rightarrow ZnSO_4 + H_2
a)
- Số mol Zn:
n_{Zn} = \frac{m_{Zn}}{M_{Zn}} = \frac{3,25}{65} = 0,05 mol
- Thể tích H_2 (đktc):
V_{H_2} = n_{H_2} * 24,79 = 0,05 * 24,79 = 1,2395 (L)
b)
- Khối lượng H_2SO_4: m_{H_2SO_4} = n_{H_2SO_4} * M_{H_2SO_4} = 0,05 * 98 = 4,9 gam
c)
- Khối lượng ZnSO_4:
m_{ZnSO_4}=n_{ZnSO_4}*M_{ZnSO_4} = 0,05 * 161 = 8,05 gam
Câu hỏi:
Câu trả lời của bạn: 17:16 18/03/2025
`\begin{cases}\frac{x}{3} = \frac{y}{9} \\2x - y = -2\end{cases}`
y = 3x
2x - (3x) = -2 \\`-x = -2 \\x = 2
y = 3(2) \\y = 6
x = 2, \quad y = 6
Câu hỏi:
Câu trả lời của bạn: 18:28 04/03/2025
1,235 × 1,236 = 1,526,460
9,999 - 2,222 + 10,000 = 17,777
888,888 + 9,998 = 898,886
1,526,460 + 17,777 + 898,886 = 2,443,123
Câu trả lời của bạn: 18:24 04/03/2025
(x - 1)^2 + (y - 3)^2 = R^2
Từ 3x + 4y + 75 = 0 :
4y = -3x - 75 \implies y = -\frac{3}{4}x - \frac{75}{4}
(x - 1)^2 + \left(-\frac{3}{4}x - \frac{75}{4} - 3\right)^2 = R^2
\left(-\frac{3}{4}x - \frac{75}{4} - 3\right) = -\frac{3}{4}x - \frac{75}{4} - \frac{12}{4} = -\frac{3}{4}x - \frac{87}{4}
\left(-\frac{3}{4}x - \frac{87}{4}\right)^2 = \left(\frac{3}{4}x + \frac{87}{4}\right)^2 = \frac{9}{16}x^2 + \frac{261}{8}x + \frac{7569}{16}
(x - 1)^2 = x^2 - 2x + 1
x^2 - 2x + 1 + \frac{9}{16}x^2 + \frac{261}{8}x + \frac{7569}{16} = R^2
\frac{16}{16}x^2 + \frac{9}{16}x^2 - \frac{32}{16}x + \frac{261}{8}x + \frac{16}{16} + \frac{7569}{16} = R^2
\frac{25}{16}x^2 + \left(-\frac{32}{16} + \frac{522}{16}\right)x + \frac{7585}{16} = R^2
\frac{25}{16}x^2 + \frac{490}{16}x + \frac{7585}{16} = R^2
\frac{25}{16}x^2 + \frac{245}{8}x + \frac{7585}{16} = R^2
Gọi M(x_1, y_1) , N(x_2, y_2) :
\overrightarrow{AM} = (x_1 - 1, y_1 - 3), \quad \overrightarrow{AN} = (x_2 - 1, y_2 - 3)
\overrightarrow{AM} \cdot \overrightarrow{AN} = (x_1 - 1)(x_2 - 1) + (y_1 - 3)(y_2 - 3) = -\frac{R^2}{2}
Vì |AM| = |AN| = R :
(x_1 - 1)^2 + (y_1 - 3)^2 = R^2, \quad (x_2 - 1)^2 + (y_2 - 3)^2 = R^2
d = \frac{|3(1) + 4(3) + 75|}{\sqrt{3^2 + 4^2}} = \frac{|90|}{5} = 18
Giải \frac{25}{16}x^2 + \frac{245}{8}x + \frac{7585}{16} = R^2 với x_1, x_2 :
\frac{25}{16}x^2 + \frac{245}{8}x + \frac{7585}{16} - R^2 = 0
Phân biệt x_1, x_2 và tìm y_1, y_2 từ 3x + 4y + 75 = 0 .
MN = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} = R\sqrt{3}
Kết hợp với \overrightarrow{AM} \cdot \overrightarrow{AN} = -\frac{R^2}{2} .
Câu trả lời của bạn: 18:20 04/03/2025
a) ----------------------------------------------
1. \text{Khối lượng muối } M_2Cho_4 = 0,255W (nếu dung dịch W g).
2. Số mol CO₂ = \frac{0,88}{44} \approx 0,02 mol → Số mol Z trong ZCO_3 = 0,02 mol.
3. Nồng độ mol Z = \frac{\text{số mol } Z}{\text{thể tích dung dịch (L)}} .
b) ---------------------------------------------------
1. 100 g khoáng → 41,5 g cặn (ZO), bay hơi 58,5 g (CO₂, H₂O).
2. Số mol CO₂ = \frac{0,88}{44} ---\approx 0,02 mol (từ 24,3 g khoáng).
3. Tính x, y, z dựa trên phản ứng và khối lượng.
c) ----------------------------------------------------
1. Nung:
- ZCO_3 \rightarrow ZO + CO_2 \uparrow
- Z(OH)_2 \rightarrow ZO + H_2O \uparrow
- tH_2O \rightarrow H_2O \uparrow
2. Tác dụng HCl:
- ZCO_3 + 2HCl \rightarrow ZCl_2 + H_2O + CO_2 \uparrow
- Z(OH)_2 + 2HCl \rightarrow ZCl_2 + 2H_2O \uparrow


