Tam giác ABC có AB = 2 cm, BC = 3 cm. Đặt CA = b (cm). a) Chứng minh rằng 1 < b < 5

Lời giải Bài 9.12 trang 52 SBT Toán 7 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

371
« Trang trước
Chia sẻ
Trang sau »
Giải SBT Toán 7 Kết nối tri thức Bài 33: Quan hệ giữa ba cạnh trong một tam giác

Bài 9.12 trang 52 SBT Toán 7 Tập 2: Tam giác ABC có AB = 2 cm, BC = 3 cm. Đặt CA = b (cm).

a) Chứng minh rằng 1 < b < 5.

b) Giả sử rằng với 1 < b < 5, có tam giác ABC thỏa mãn AB = 2 cm, BC = 3 cm, CA = b (cm). Với mỗi tam giác đó, hãy sắp xếp ba góc A, B, C theo thứ tự từ bé đến lớn.

Lời giải:

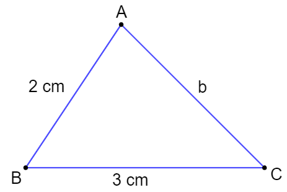
Sách bài tập Toán 7 Bài 33 (Kết nối tri thức): Quan hệ giữa ba cạnh trong một tam giác (ảnh 1)

a) Theo bất đẳng thức tam giác, ta có:

BC − AB < AC < BC + AB

Hay 3 − 2 < b < 3 + 2

Do đó 1 < b < 5 (đpcm).

b)

+) Với 1 < b ≤ 2, ta có: AC ≤ AB < BC.

Xét tam giác ABC có AC ≤ AB < BC nên suy ra B^≤C^<A^ .

+) Với 2 < b ≤ 3, ta có: AB ≤ AC < BC.

Xét tam giác ABC có AB ≤ AC < BC nên suy ra C^≤B^<A^ .

+) Với 3 < b < 5, ta có: AB ≤ BC < AC.

Xét tam giác ABC có AB ≤ BC < AC nên suy ra C^≤A^<B^ .

Xem thêm các bài giải sách bài tập Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

Bài viết liên quan

371
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm

    Bài viết có lượt xem cao