Hãy giải thích tại sao trong tam giác vuông, cạnh huyền dài nhất và trong tam giác tù

Lời giải Bài 9.3 trang 48 SBT Toán 7 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

164
« Trang trước
Chia sẻ
Trang sau »
Giải SBT Toán 7 Kết nối tri thức Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác

Bài 9.3 trang 48 SBT Toán 7 Tập 2: Hãy giải thích tại sao trong tam giác vuông, cạnh huyền dài nhất và trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

Lời giải:

Gọi tam giác ABC vuông tại A và tam giác MNP là tam giác tù tại đỉnh M.

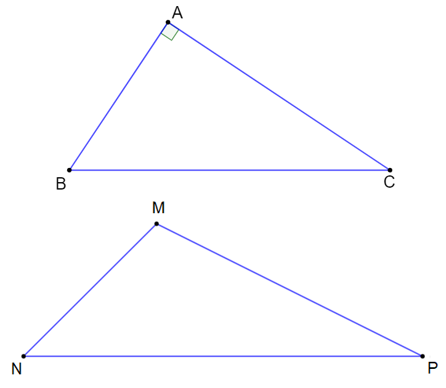
Sách bài tập Toán 7 Bài 31 (Kết nối tri thức): Quan hệ giữa góc và cạnh đối diện trong một tam giác (ảnh 1)

+) Giả sử tam giác ABC là tam giác vuông tại đỉnh A nên suy ra A^=90°  (1)

Lại có tam giác ABC có tổng ba góc trong tam giác bằng 180º nên suy ra: A^+B^+C^=180°

Hay A^=180°−B^+C^

Vậy suy ra  180°−B^+C^=90°⇔B^+C^=90°

Hay ta suy ra được 0°<B^<90°  và  0°<C^<90°(2)

Từ (1) và (2) ta có:

Theo định lí 2 ta có BC > AC và BC > AB nên BC là cạnh lớn nhất

Vậy trong tam giác vuông, cạnh huyền là cạnh lớn nhất (đpcm).

+) Giả sử tam giác MNP là tam giác tù tại đỉnh M nên suy ra 90°<M^<180°  (3)

Lại có tam giác MNP có tổng ba góc trong tam giác bằng 180º nên suy ra: M^+N^+P^=180°

Hay M^=180°−N^+P^

Suy ra 90°<180°−N^+P^<180°

Do đó 0°<N^+P^<90°

Hay ta suy ra được 0°<N^<90°  và  0°<P^<90°(4)

Từ (3) và (4) ta có: M^>N^;   M^>P^ .

Theo định lí 2 ta có NP > MP và NP > MN nên NP là cạnh lớn nhất.

Vậy trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất (đpcm).

Xem thêm các bài giải sách bài tập Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

Bài viết liên quan

164
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm

    Bài viết có lượt xem cao