Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AB = AD
Lời giải Bài 96 trang 97 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 96 trang 97 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AB = AD. Vẽ BE vuông góc với CD tại E. Gọi I là giao điểm của AC và BE; K là hình chiếu của I trên BC.
a) Chứng minh ba điểm D, I, K thẳng hàng.
b) Tìm điều kiện của tam giác ABC để I là trọng tâm của tam giác BCD.
Lời giải
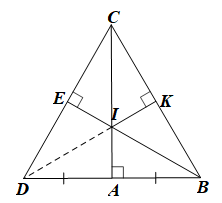
a) Xét tam giác BCD có I là giao điểm của hai đường cao CA và BE nên I là trực tâm của tam giác DBC.
Suy ra DI ⊥ BC.
Mặt khác, IK ⊥ BC (giả thiết).
Do đó đường cao DI đi qua K nên ba điểm D, I, K thẳng hàng.
Vậy ba điểm D, I, K thẳng hàng.
b) Xét CDA và CBA có:
,
CA là cạnh chung,
AD = AB (giả thiết)
Do đó CDA = CBA (hai cạnh góc vuông)
Suy ra CD = CB (hai cạnh tương ứng) (1)
Tam giác BCD có I là trọng tâm của tam giác nên BE là đường trung tuyến của tam giác.
Do đó CE = DE.
Chứng minh tương tự như trên ta cũng có BDE = BCE (hai cạnh góc vuông)
Suy ra BD = BC (hai cạnh tương ứng) (2)
Từ (1) và (2) ta có BC = CD = DB nên tam giác BCD là tam giác đều.
Do đó hay
Vậy điều kiện của tam giác ABC để I cũng là trọng tâm của tam giác BCD là tam giác ABC vuông tại A có .
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
