Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh độ dài AD và DC
Lời giải Bài 57 trang 86 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 57 trang 86 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh độ dài AD và DC.
Lời giải
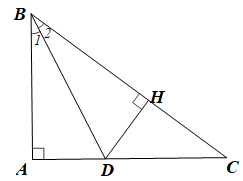
Kẻ DH ⊥ BC.
Vì BD là tia phân giác của góc ABC nên .
Xét DAB và DHB có:
,
BD là cạnh chung,
(chứng minh trên)
Do đó ∆DAB = ∆DHB (cạnh huyền – góc nhọn).
Suy ra AD = HD (hai cạnh tương ứng) (1)
Vì DDHC vuông tại H nên HD < DC (trong tam giác vuông, cạnh huyển là cạnh lớn nhất) (2)
Từ (1) và (2) suy ra AD < DC.
Vậy AD < DC.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài 52 trang 85 SBT Toán 7 Tập 2: Cho góc xOy và điểm B thuộc tia Ox, B ≠ O. Vẽ H là hình chiếu của điểm B trên đường thẳng Oy trong các trường hợp sau: a) là góc nhọn...
Bài 53 trang 85 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A có H là hình chiếu của A trên đường thẳng BC, lấy điểm M nằm giữa A và H. Chứng minh: a) BH = CH...
Bài 55 trang 85 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A, M là trung điểm của AC. a) Vẽ E là hình chiếu của A trên đường thẳng BM...
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
