Cho tam giác MNP cân tại P. Lấy điểm A trên cạnh PM, điểm B trên cạnh PN sao cho PA = PB
Lời giải Bài 47 trang 83 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 47 trang 83 SBT Toán 7 Tập 2: Cho tam giác MNP cân tại P. Lấy điểm A trên cạnh PM, điểm B trên cạnh PN sao cho PA = PB. Gọi O là giao điểm của NA và MB. Chứng minh tam giác OMN là tam giác cân.
Lời giải
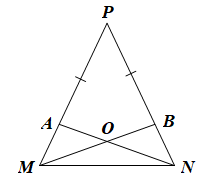
Vì MNP cân tại P nên ta có:
PM = PN (hai cạnh bên), (hai góc ở đáy).
Ta có PM = PA + AM, PN = PB + BN.
Mà PM = PN (chứng minh trên), PA = PB (giả thiết).
Suy ra AM = BN.
Xét AMN và BNM có:
AM = BN (chứng minh trên),
MN là cạnh chung,
(do )
Do đó ∆AMN = ∆BNM (c.g.c).
Suy ra (hai góc tương ứng).
Hay
Do đó tam giác ONM cân tại O.
Vậy tam giác OMN là tam giác cân tại O.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài 44 trang 83 SBT Toán 7 Tập 2: Ở Hình 36 có AB song song cới CD, BC song song với AD. Tia phân giác của góc BAD cắt BC tại E và cắt tia DC tại F...
Bài 45 trang 83 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A có . Trên tia đối của tia CB lấy điểm M sao cho AC = CM. Tính số đo mỗi góc của tam giác ABM...
Bài 46 trang 83 SBT Toán 7 Tập 2: Cho tam giác ABC. Gọi I là trung điểm của BC. Tính số đo góc BAC, biết IA = IB = IC...
Bài 47 trang 83 SBT Toán 7 Tập 2: Cho tam giác MNP cân tại P. Lấy điểm A trên cạnh PM, điểm B trên cạnh PN sao cho PA = PB. Gọi O là giao điểm của NA và MB. Chứng minh tam giác OMN là tam giác cân...
Bài 48 trang 83 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A có . Trên cạnh BC lấy các điểm D, E sao cho BD = BA, CE = CA...
Bài 49 trang 83 SBT Toán 7 Tập 2: Cho Hình 37 có AB = AC = BC = BD = CE, . a) Chứng minh tam giác AED là tam giác cân...
Bài 50 trang 84 SBT Toán 7 Tập 2: Cho tam giác đều ABC. Gọi E, D, F là ba điểm lần lượt nằm trên ba cạnh AB, AC, BC sao cho AD = CF = BE. Chứng minh tam giác DEF là tam giác đều...
Bài 51* trang 84 SBT Toán 7 Tập 2: Cho tam giác ABC. Trên cạnh BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho CE = BD. Gọi O là giao điểm của DE và BC. Biết OD = OE. Chứng minh tam giác ABC là tam giác cân...
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
