Cho Hình 32 có góc BAC bằng 90 độ , AH vuông góc với BC tại H
Lời giải Bài 40 trang 81 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 40 trang 81 SBT Toán 7 Tập 2: Cho Hình 32 có , AH vuông góc với BC tại H, , Ay là tia đối của tia Ax. BD và CE vuông góc với xy lần lượt tại D và E. Chứng minh:
a) AC là tia phân giác của góc Hay;
b) BD + CE = BC;
c) DH vuông góc với HE.
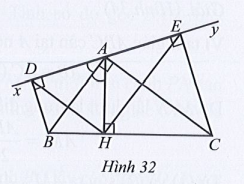
Lời giải
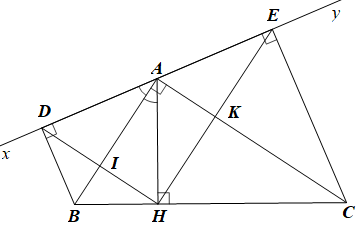
a) • Ta có
Hay
Suy ra
• Ta có
Nên
Mà (giả thiết)
Suy ra
Do đó AC là tia phân giác của
Vậy AC là tia phân giác của .
b) • Xét ABD và ABH có:
,
AB là cạnh chung,
(giả thiết),
Do đó ∆ABD = ∆ABH (cạnh huyền – góc nhọn).
Suy ra BD = BH , AD = AH (các cặp cạnh tương ứng).
• Xét ACE và DACH có:
,
AC là cạnh chung,
(chứng minh câu a),
Do đó ∆ACE = ∆ACH (cạnh huyền – góc nhọn).
Suy ra CE = CH, AE = AH (các cặp cạnh tương ứng).
• Ta có BC = BH + CH
Mà BD = BH, CE = CH.
Do đó BC = BD + CE.
Vậy BC = BD + CE.
c) Gọi I là giao điểm của AB và DH, K là giao điểm của EH và AC.
• Xét ∆ADI và ∆AHI có:
AD = AH (chứng minh câu b),
(do ),
AI là cạnh chung.
Do đó ∆ADI = ∆AHI (c.g.c).
Suy ra (hai góc tương ứng).
Hay .
• Xét ∆AHK và ∆AEK có:
AH = AE (chứng minh câu b),
(do ),
AK là cạnh chung
Do đó ∆AHK = ∆AEK (c.g.c)
Suy ra (hai góc tương ứng).
Hay .
Xét ADH có: (tổng ba góc của một tam giác).
Mà nên
Xét AEH có: (tổng ba góc của một tam giác)
Mà nên
Ta có
Suy ra DH ⊥ HE.
Vậy DH ⊥ HE.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
