Cho ∆ABC = ∆A’B’C’. Vẽ AH vuông góc với BC tại H, A’H’ vuông góc với B’C’ tại H’
Lời giải Bài 38 trang 81 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Giải SBT Toán 7 Cánh diều Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
Bài 38 trang 81 SBT Toán 7 Tập 2: Cho ∆ABC = ∆A’B’C’. Vẽ AH vuông góc với BC tại H, A’H’ vuông góc với B’C’ tại H’. Chứng minh AH = A’H’.
Lời giải
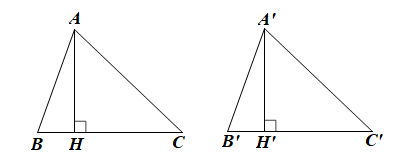
Do ∆ABC = ∆A’B’C’ (giả thiết)
Nên AB = A’B’ (hai cạnh tương ứng) và (hai góc tương ứng).
Xét ∆ABH và ∆AB’H’ có:
,
AB = A’B’ (chứng minh trên),
(do )
Suy ra ∆ABH = ∆A’B’H’ (cạnh huyền – góc nhọn).
Do đó AH = A’H’ (hai cạnh tương ứng).
Vậy AH = A’H’.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
