Xét tam giác ABC vuông tại A; đường phân giác góc B cắt cạnh AC tại E
Lời giải Bài 9.25 trang 60 SBT Toán 7 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 9.25 trang 60 SBT Toán 7 Tập 2: Xét tam giác ABC vuông tại A; đường phân giác góc B cắt cạnh AC tại E; đường thẳng qua E vuông góc với BC cắt đường thẳng AB tại K. Chứng minh:
a) AE < EC;
b) BK = BC.
Lời giải:
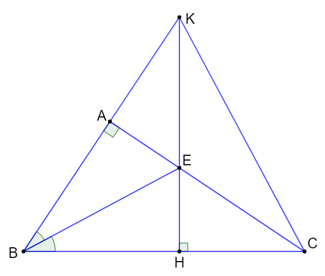
a) Đường thẳng EK cắt BC tại H.
Do E nằm trên đường thẳng BE là đường phân giác của góc KBC nên EA = EH.
Mà trong tam giác EHC là tam giác vuông tại H có EH < EC (do EC là cạnh huyền).
Từ đó ta suy ra được: AE < EC (đpcm).
b) E là giao của hai đường cao CA VÀ KH của tam giác BKC nên E là trực tâm của tam giác BKC.
Từ đó suy ra BE cũng là đường cao của tam giác BKC.
Do đó BE vừa là đường phân giác, vừa là đường cao của tam giác BKC.
Nên suy ra tam giác BKC cân tại B.
Vậy BK = BC (đpcm).
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:
Câu 1 trang 59 SBT Toán 7 Tập 2: Tìm phương án sai trong câu sau: Trong tam giác A. đối diện với góc lớn nhất là cạnh lớn nhất...
Câu 2 trang 59 SBT Toán 7 Tập 2: Bộ ba số nào sau đây không là độ dài ba cạnh của một tam giác?...
Câu 3 trang 59 SBT Toán 7 Tập 2: Tam giác cân có độ dài cạnh bên b; độ dài cạnh đáy d thì ta phải có...
Câu 4 trang 59 SBT Toán 7 Tập 2: Với mọi tam giác ta đều có: A. mỗi cạnh lớn hơn nửa chu vi B. mỗi cạnh lớn hơn hoặc bằng nửa chu vi...
Câu 5 trang 59 SBT Toán 7 Tập 2: Xét hai đường trung tuyến BM, CN của tam giác ABC có BC = 4 cm. Trong các số sau, số nào có thể là tổng độ dài BM + CN?...
Câu 6 trang 59 SBT Toán 7 Tập 2: Tam giác ABC có số đo ba góc thỏa mãn . Hai tia phân giác của góc A và góc B cắt nhau tại điểm I. Khi đó góc BIC có số đo là...
Bài 9.23 trang 59 SBT Toán 7 Tập 2: Cho D là một điểm bên trong tam giác ABC. Chứng minh: a) ...
Bài 9.24 trang 60 SBT Toán 7 Tập 2: Cho M là một điểm tùy ý bên trong tam giác đều ABC. Lấy điểm N nằm khác phía với M đối với đường thẳng AC sao cho và AN = AM. Chứng minh...
Bài 9.25 trang 60 SBT Toán 7 Tập 2: Xét tam giác ABC vuông tại A; đường phân giác góc B cắt cạnh AC tại E; đường thẳng qua E vuông góc với BC cắt đường thẳng AB tại K. Chứng minh...
Bài 9.26 trang 60 SBT Toán 7 Tập 2: Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng vuông góc với AB tại A và tại B. Một đường thẳng qua C cắt Ax tại M, cắt By tại P...
Bài viết liên quan
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 32: Quan hệ giữa đường vuông góc và đường xiên
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 33: Quan hệ giữa ba cạnh trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Ôn tập chương 9
