Cho D là một điểm bên trong tam giác ABC. Chứng minh

Lời giải Bài 9.23 trang 59 SBT Toán 7 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

164
« Trang trước
Chia sẻ
Trang sau »
Giải SBT Toán 7 Kết nối tri thức Ôn tập chương 9

Bài 9.23 trang 59 SBT Toán 7 Tập 2: Cho D là một điểm bên trong tam giác ABC. Chứng minh:

a) BDC^>BAC^ ;

b) BD + DC < AB + AC.

Lời giải:

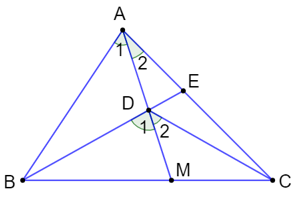
Sách bài tập Toán 7 (Kết nối tri thức) Ôn tập chương 9 (ảnh 1)

a) Tia AD chia góc A thành góc A1 và góc A2, chia cóc BDC thành góc D1 và góc D2 như hình vẽ trên.

Xét tam giác BDM có: D^1=A^1+ABD^  nên D^1>A^1 .

Xét tam giác CDM có: D^2=A^2+ACD^  nên D^2>A^2

Nên suy ra D^=D^1+D^2>A^1+A^2=A^  (đpcm).

b) Lấy E là giao điểm của BD và AC.

Ta có: AB + AC = AB + AE + EC (1)

Trong tam giác ABE, theo bất đẳng thức tam giác ta có: AB + AE > BE (2)

Từ (1) và (2) suy ra: AB + AC > BE + EC = BD + DE + EC (3)

Trong tam giác CDE, theo bất đẳng thức tam giác ta có: DE + EC > DC (4)

Từ (3) và (4) suy ra: AB + AC > BD + DC (đpcm).

Xem thêm các bài giải sách bài tập Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

Câu 1 trang 59 SBT Toán 7 Tập 2: Tìm phương án sai trong câu sau: Trong tam giác A. đối diện với góc lớn nhất là cạnh lớn nhất...

Câu 2 trang 59 SBT Toán 7 Tập 2: Bộ ba số nào sau đây không là độ dài ba cạnh của một tam giác?...

Câu 3 trang 59 SBT Toán 7 Tập 2: Tam giác cân có độ dài cạnh bên b; độ dài cạnh đáy d thì ta phải có...

Câu 4 trang 59 SBT Toán 7 Tập 2: Với mọi tam giác ta đều có: A. mỗi cạnh lớn hơn nửa chu vi B. mỗi cạnh lớn hơn hoặc bằng nửa chu vi...

Câu 5 trang 59 SBT Toán 7 Tập 2: Xét hai đường trung tuyến BM, CN của tam giác ABC có BC = 4 cm. Trong các số sau, số nào có thể là tổng độ dài BM + CN?...

Câu 6 trang 59 SBT Toán 7 Tập 2: Tam giác ABC có số đo ba góc thỏa mãn  A^=B^+C^ . Hai tia phân giác của góc A và góc B cắt nhau tại điểm I. Khi đó góc BIC có số đo là...

Bài 9.23 trang 59 SBT Toán 7 Tập 2: Cho D là một điểm bên trong tam giác ABC. Chứng minh: a) BDC^>BAC^ ...

Bài 9.24 trang 60 SBT Toán 7 Tập 2: Cho M là một điểm tùy ý bên trong tam giác đều ABC. Lấy điểm N nằm khác phía với M đối với đường thẳng AC sao cho    và AN = AM. Chứng minh...

Bài 9.25 trang 60 SBT Toán 7 Tập 2: Xét tam giác ABC vuông tại A; đường phân giác góc B cắt cạnh AC tại E; đường thẳng qua E vuông góc với BC cắt đường thẳng AB tại K. Chứng minh...

Bài 9.26 trang 60 SBT Toán 7 Tập 2: Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng vuông góc với AB tại A và tại B. Một đường thẳng qua C cắt Ax tại M, cắt By tại P...

Bài viết liên quan

164
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm

    Bài viết có lượt xem cao