Cho tam giác ABC với M là trung điểm của BC. Lấy điểm N sao cho C là trung điểm
Lời giải Bài 9.18 trang 55 SBT Toán 7 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 9.18 trang 55 SBT Toán 7 Tập 2: Cho tam giác ABC với M là trung điểm của BC. Lấy điểm N sao cho C là trung điểm của đoạn thẳng BN. Lấy điểm P sao cho M là trung điểm của đoạn thẳng AP. Chứng minh đường thẳng AC đi qua trung điểm của PN, đường thẳng PC đi qua trung điểm của AN.
Lời giải:
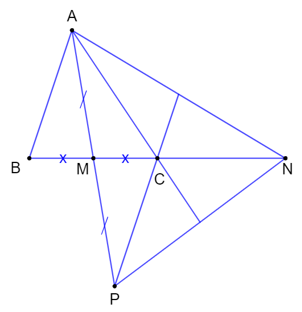
Trong tam giác ANP có đường trung tuyến NM và NC = BC = 2CM nên C là trọng tâm của tam giác ANP.
Do đó AC, PC là hai đường tung tuyến của tam giác ANP.
Vậy AC đi qua trung điểm của PN và PC đi qua trung điểm của AN.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:
Bài 9.14 trang 55 SBT Toán 7 Tập 2: Cho góc xAy và một điểm G trong góc đó. Lấy hai điểm M, N trên tia AG sao cho . Qua N kẻ đường thẳng song song với đường thẳng chứa tia Ax, nó cắt Ay tại C. Đường thẳng CM cắt Ax tại B...
Bài 9.15 trang 55 SBT Toán 7 Tập 2: Gọi M là trung điểm của cạnh BC của tam giác ABC và D là điểm sao cho M là trung điểm của AD. Đường thẳng qua D và trung điểm của AB cắt BC tại U, đường thẳng qua D và trung điểm của AC cắt BC tại V. Chứng minh BU = UV = VC...
Bài 9.16 trang 55 SBT Toán 7 Tập 2: a) Gọi I là giao điểm của hai đường phân giác BE và CF của tam giác ABC. Đường thẳng qua I song song với BC cắt AB tại J và cắt AC tại K. Chứng minh JK = BJ + CK...
Bài 9.17 trang 55 SBT Toán 7 Tập 2: Tam giác ABC có AD, BE là hai đường phân giác và . Chứng minh rằng DE là tia phân giác của góc ADC...
Bài 9.18 trang 55 SBT Toán 7 Tập 2: Cho tam giác ABC với M là trung điểm của BC. Lấy điểm N sao cho C là trung điểm của đoạn thẳng BN. Lấy điểm P sao cho M là trung điểm của đoạn thẳng AP...
Bài viết liên quan
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 32: Quan hệ giữa đường vuông góc và đường xiên
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 33: Quan hệ giữa ba cạnh trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Ôn tập chương 9
