Gọi M là trung điểm của cạnh BC của tam giác ABC và D là điểm sao cho M là trung điểm của AD
Lời giải Bài 9.15 trang 55 SBT Toán 7 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 9.15 trang 55 SBT Toán 7 Tập 2: Gọi M là trung điểm của cạnh BC của tam giác ABC và D là điểm sao cho M là trung điểm của AD. Đường thẳng qua D và trung điểm của AB cắt BC tại U, đường thẳng qua D và trung điểm của AC cắt BC tại V. Chứng minh BU = UV = VC.
Lời giải:
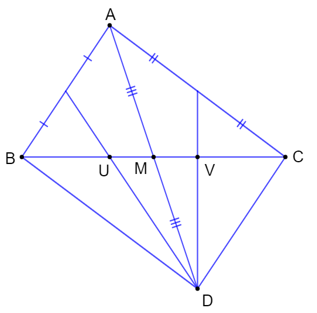
+) Tam giác BAC có M là trung điểm của BC nên suy ra MB = MC (1)
+) Xét tam giác ABD có U là giao của 2 đường trung tuyến BM và DE nên U là trọng tâm tam giác ABD
Vậy áp dụng định lí 1 ta có:
Suy ra (2)
Từ đó ta có: (3)
+) Xét tam giác ACD có V là giao của 2 đường trung tuyến CM và DF nên V là trọng tâm tam giác AVD
Vậy áp dụng định lí 1 ta có:
Suy ra (4)
Từ đó ta có: (5)
Từ (1), (3), (5) ta có:
(6)
Từ (1), (2), (4), (6) ta có: (đpcm).
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:
Bài 9.14 trang 55 SBT Toán 7 Tập 2: Cho góc xAy và một điểm G trong góc đó. Lấy hai điểm M, N trên tia AG sao cho . Qua N kẻ đường thẳng song song với đường thẳng chứa tia Ax, nó cắt Ay tại C. Đường thẳng CM cắt Ax tại B...
Bài 9.15 trang 55 SBT Toán 7 Tập 2: Gọi M là trung điểm của cạnh BC của tam giác ABC và D là điểm sao cho M là trung điểm của AD. Đường thẳng qua D và trung điểm của AB cắt BC tại U, đường thẳng qua D và trung điểm của AC cắt BC tại V. Chứng minh BU = UV = VC...
Bài 9.16 trang 55 SBT Toán 7 Tập 2: a) Gọi I là giao điểm của hai đường phân giác BE và CF của tam giác ABC. Đường thẳng qua I song song với BC cắt AB tại J và cắt AC tại K. Chứng minh JK = BJ + CK...
Bài 9.17 trang 55 SBT Toán 7 Tập 2: Tam giác ABC có AD, BE là hai đường phân giác và . Chứng minh rằng DE là tia phân giác của góc ADC...
Bài 9.18 trang 55 SBT Toán 7 Tập 2: Cho tam giác ABC với M là trung điểm của BC. Lấy điểm N sao cho C là trung điểm của đoạn thẳng BN. Lấy điểm P sao cho M là trung điểm của đoạn thẳng AP...
Bài viết liên quan
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 32: Quan hệ giữa đường vuông góc và đường xiên
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 33: Quan hệ giữa ba cạnh trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Ôn tập chương 9
