Tìm n ∈ ℤ để 2n^2 – n chia hết cho n + 1
Lời giải Bài 48* trang 54 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 48* trang 54 SBT Toán 7 Tập 1:
Tìm n ∈ ℤ để 2n2 – n chia hết cho n + 1.
Lời giải
Ta thực hiện đặt tính chia đa thức như sau:
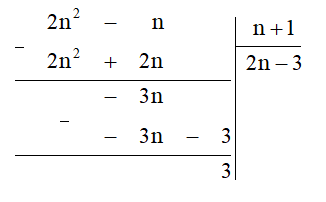
Do đó (với n + 1 ≠ 0).
Với n ∈ ℤ để 2n2 – n chia hết cho n + 1 thì 3 ⋮ (n + 1).
Điều này xảy ra khi và chỉ khi (n + 1) ∈ Ư(3) = {–1; 1; –3; 3}.
Ta có bảng sau:
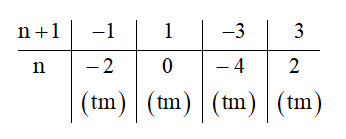
Vậy n ∈ {–4; –2; 0; 3}.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài 41 trang 53 SBT Toán 7 Tập 1: Tính: a) b) (5xn) : (4x2) (n ∈ ℕ, n ≥ 2)...
Bài 42 trang 53, 54 SBT Toán 7 Tập 1: a) Cho đa thức Rút gọn rồi tính giá trị của P(x) tại x = –2...
Bài 43 trang 54 SBT Toán 7 Tập 1: Khi giải bài tập “Xét xem đa thức A(x) = – 12x4 + 5x3 + 15x2 có chia hết cho đơn thức B(x) = 3x2 hay không”, bạn Hồng nói “Đa thức A(x) không chia hết cho đơn thức B(x) vì 5 không chia hết cho 3”...
Bài 44 trang 54 SBT Toán 7 Tập 1: Tính: a) (3x3 – 7x2 + 4x – 4) : (x – 2); b) (x5 + x + 1) : (x3 – x)...
Bài 45 trang 54 SBT Toán 7 Tập 1: Cho đa thức P(x) = 3x3 – 2x2 + 5. Chia đa thức P(x) cho đa thức Q(x) (Q(x) ≠ 0) được thương là đa thức S(x) = 3x – 2 và dư là đa thức R(x) = 3x + 3. Tìm đa thức Q(x)...
Bài 46 trang 54 SBT Toán 7 Tập 1: a) Tìm số dư của phép chia đa thức 4x4 – 2x2 + 7 cho x + 3. b) Tìm đa thức bị chia, biết đa thức chia là x2 – 2x + 3, thương là x2 – 2, dư là 9x – 5...
Bài 47 trang 54 SBT Toán 7 Tập 1: a) Tìm số a sao cho 10x2 – 7x + a chia hết cho 2x – 3. b) Tìm số a sao cho x3 – 10x + a chia hết cho x – 2...
Bài 48* trang 54 SBT Toán 7 Tập 1: Tìm n ∈ ℤ để 2n2 – n chia hết cho n + 1...
Bài 49 trang 54 SBT Toán 7 Tập 1: Một mảnh đất có dạng hình thang vuông với đáy bé là 10 m, chiều cao là 2x + 5 (m). Người ta mở rộng mảnh đất đó để được mảnh đất có dạng hình chữ nhật như Hình 6...
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 2: Đa thức một biến. Nghiệm của đa thức một biến
- Giải Sách bài tập Toán 7 Cánh diều Bài 3: Phép cộng, phép trừ đa thức một biến
- Giải Sách bài tập Toán 7 Cánh diều Bài 4: Phép nhân đa thức một biến
- Giải Sách bài tập Toán 7 Cánh diều Bài 5: Phép chia đa thức một biến
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 6
