Bài tập cuối chương 6

Bộ 15 Bài tập cuối chương 6 có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài tập cuối chương 6.

347

Tải tài liệu

« Trang trước

Trang sau »

Trắc nghiệm Toán 10 Bài tập cuối chương 6 - Cánh diều

Câu 1. Trong một kì thi vấn đáp thí sinh đứng trước ban giám khảo chọn 3 phiếu câu hỏi từ một thùng phiếu gồm 50 câu hỏi, trong đó có 4 cặp phiếu câu hỏi mà mỗi cặp phiếu có nội dung khác nhau từng đôi một và trong mỗi một cặp phiếu có nội dung giống nhau. Tính xác suất để thí sinh chọn được 3 phiếu câu hỏi có nội dung khác nhau.

A. $\frac{3}{4}$ ;

B. $\frac{12}{1225}$ ;

C. $\frac{4}{7}$ ;

D. $\frac{1213}{1225}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: Mỗi lần chọn 3 câu hỏi ngẫu nhiên từ 50 câu hỏi cho ta một tổ hợp chập 3 của 50 nên n(Ω) = $C_{50}^{3}$

Gọi F là biến cố:” thí sinh chọn được 3 phiếu câu hỏi có nội dung khác nhau”

⇒ $\bar{F}$ là biến cố” thí sinh chọn được 3 phiếu câu hỏi trong đó có 1 cặp câu hỏi có nội dung giống nhau”

Việc thí sinh chọn được 3 phiếu câu hỏi trong đó có 1 cặp câu hỏi có nội dung giống nhau có thể xem là một công việc có 2 công đoạn:

- Công đoạn 1: Chọn 1 cặp trong 4 cặp câu hỏi giống nhau có $C_{4}^{1}$ = 4 cách

- Công đoạn 2: Chọn 1 phiếu câu hỏi trong 48 phiếu còn lại: có 48 cách chọn

Do đó, n( $\bar{F}$ ) = 4.48 = 192 cách chọn

⇒P( $\bar{F}$ ) = $\frac{n (\bar{F})}{n (Ω)}$ = $\frac{192}{19600}$ = $\frac{12}{1225}$

⇒ P(F) = 1 - P( $\bar{F}$ ) = 1 - $\frac{12}{1225}$ = $\frac{1213}{1225}$

Câu 2. Số áo bán được trong một quý ở cửa hàng bán áo sơ mi được thống kê như sau:

Cỡ áo

Tần số

(số áo bán được)

126

125

110

Giá trị mốt của bảng phân bố tần số trên bằng

A. 38;

B. 126;

C. 39;

D. 12.

Hiển thị đáp án

Đáp án: A

Giải thích:

Theo bảng tần số trên thì cỡ áo 38 bán được với số lượng nhiều nhất trong một quý . Nên mốt của mẫu số liệu là 38

Câu 3. Tiền lương hàng tháng của 7 nhân viên trong một công ty du lịch lần lượt là 6,5; 8,4; 6,9; 7,2; 2,5; 6,7; 3,0 (đơn vị: triệu đồng). Trung vị của mẫu số liệu trên là

A. 6,8 triệu đồng;

B. 7,2 triệu đồng;

C. 6,7 triệu đồng;

D. 6,9 triệu đồng.

Hiển thị đáp án

Đáp án: C

Giải thích:

Sắp xếp các số liệu theo thứ tự tăng dần ta được: 2,5; 3,0; 6,5; 6,7; 6,9; 7,2; 8,4

Ta thấy bảng số liệu trên có 7 giá trị nên trung vị là số liệu đứng ở vị trí 4

Vậy trung vị M_e = 6,7.

Câu 4. Kết quả kiểm tra 15 phút môn toán của 100 học sinh được trình bày ở bảng sau:

Điểm	3	4	5	6	7	8	9	10
Số học sinh	3	5	11	17	30	19	10	5

Điểm trung bình môn Toán của các học sinh nói trên là:

A. 6,88;

B. 7,12;

C. 6,5;

D. 7,22.

Hiển thị đáp án

Đáp án: A

Giải thích:

\bar{x} = \frac{3.3 + 4.5 + 5.11 + 6.17 + 7.30 + 8.19 + 9.10 + 10.5}{100}

= 6,88

Câu 5. Cho dãy số liệu thống kê:1; 2; 3; 4; 5; 6; 7. Phương sai của mẫu số liệu trên là

A. 1;

B. 2;

C. 3;

D. 4.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $\bar{x} = \frac{1 + 2 + 3 + 4 + 5 + 6 + 7}{7} = 4$

s² = $\frac{{(1 - 4)}^{2} + {(2 - 4)}^{2} + {(3 - 4)}^{2} + {(4 - 4)}^{2} + {(5 - 4)}^{2} + {(6 - 4)}^{2} + {(7 - 4)}^{2}}{7}$ = 4

Câu 6. Nếu đơn vị đo của số liệu là kg thì đơn vị của độ lệch chuẩn là

A. $\frac{k g}{2}$ ;

B. Không có đơn vị;

C. kg²;

D. kg.

Hiển thị đáp án

Đáp án: D

Giải thích:

Độ lệch chuẩn của số liệu thống kê có cùng đơn vị với đơn vị của các số liệu trong mẫu thống kê.

Câu 7. Theo kết quả thống kê điểm thi giữa kì 2 môn toán khối 10 của một trường THPT , người ta tính được phương sai của mẫu số liệu đó là s² = 0,64. Độ lệch chuẩn của mẫu số liệu đó bằng:

A. 0,4096;

B. 0,77;

C. 0,8;

D. 0,64.

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có s

\sqrt{s^{2}} = \sqrt{0, 64}

= 0,8

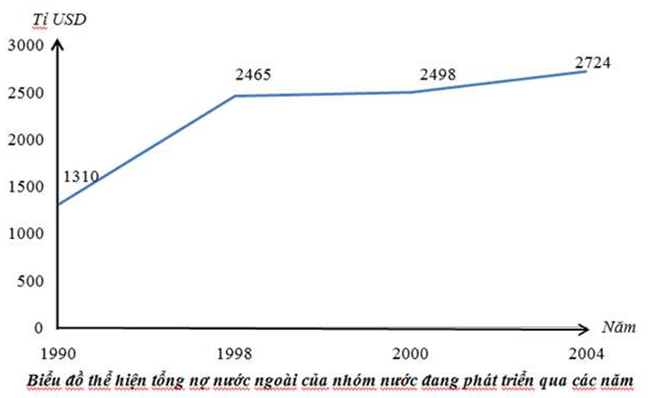
Câu 8. Biểu đồ sau thể hiện tổng nợ nước ngoài của nhóm nước đang phát triẻn trong giai đoạn 1990 đến 2004. Hãy tìm khoảng biến thiên của mẫu số liệu đó.

15 Bài tập trắc nghiệm Toán 10 Chương 6 Cánh diều có lời giải

A. 2724;

B. 1414;

C. 1310;

D. 4034.

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: x_max = 2724 và x_min = 1310 ⇒ R = x_max - x_min = 2724 – 1310 = 1414.

Câu 9. Gieo 1 con xúc xắc . Số phần tử của không gian mẫu là:

A. 5;

B. 6;

C. 8;

D. 0.

Hiển thị đáp án

Đáp án: B

Giải thích:

Ω = {1; 2; 3; 4; 5; 6} ⇒ n(Ω) = 6

Câu 10. Cho A và $\bar{A}$ là hai biến cố đối nhau. Chọn câu đúng.

A. P(A) = 1 + P( $\bar{A}$ );

B. P(A) = P( $\bar{A}$ );

C. P(A) = 1 − P( $\bar{A}$ );

D. P(A) + P( $\bar{A}$ ) = 0.

Hiển thị đáp án

Đáp án: C

Giải thích:

Câu 11. Một hộp có 5 viên bi đỏ và 9 viên bi xanh. Chọn ngẫu nhiên 2 viên bị. Xác suất để chọn được hai viên bi khác màu là:

A. $\frac{14}{45}$ ;

B. $\frac{45}{91}$ ;

C. $\frac{46}{91}$ ;

D. $\frac{15}{22}$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: Mỗi lần chọn 2 viên bi ngẫu nhiên từ 14 viên bi cho ta một tổ hợp chập 2 của 14 nên n(Ω) = $C_{14}^{2}$ = 91

Gọi A là biến cố: “Hai viên bi được chọn khác màu”

Việc chọn 2 viên bi từ hộp sao cho hai viên bi được chọn khác màu có thể xem là 1 công việc gồm 2 công đoạn:

+ Công đoạn 1: Chọn 1 viên bi màu đỏ có 5 cách

+ Công đoạn 2: Chọn 1 viên bi màu xanh có 9 cách

⇒n(A) = 5.9 = 45

P(A) = $\frac{n (A)}{n (Ω)}$ = $\frac{45}{91}$

Câu 12. Cho tam giác ABC có độ dài ba cạnh:

a = 13cm ± 0,2cm; b = 11, 2cm ± 0,2cm; c = 7cm ± 0,1cm. Tính chu vi P của tam giác đã cho.

A. P = 31, 2cm ± 0, 2cm;

B. P = 31, 2cm ± 1cm;

C. P = 31, 2cm ± 0, 5cm;

D. P = 31, 2cm ± 2cm.

Hiển thị đáp án

Đáp án: C

Giải thích:

Chu vi tam giác là:

P = a + b + c = (13 + 11, 2 + 7) ± (0,2 + 0,2 + 0,1) = 31, 2 ± 0,5.

Câu 13. Một hộp có 5 viên bi đỏ, 3 viên bi vàng và 4 viên bi xanh. Chọn ngẫu nhiên từ hộp 4 viên bi, tính xác suất để 4 viên bi được chọn có số bi đỏ lớn hơn số bi vàng và nhất thiết phải có mặt bi xanh.

A. $\frac{1}{12}$ ;

B. $\frac{1}{3}$ ;

C. $\frac{16}{33}$ ;

D. $\frac{1}{2}$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: Mỗi lần chọn 4 viên bi ngẫu nhiên từ 12 viên bi cho ta một tổ hợp chập 4 của 12 nên n(Ω) = $C_{12}^{4}$ = 495

Gọi D là biến cố:” 4 viên bi được chọn có số bi đỏ lớn hơn số bi vàng và nhất thiết phải có mặt bi xanh”

- Trường hợp 1: Chọn 1 bi đỏ và 3 bi xanh có $C_{5}^{1} . C_{4}^{3}$ = 20 cách

- Trường hợp 2: Chọn 2 bi đỏ và 2 bi xanh có $C_{5}^{2} . C_{4}^{2}$ = 60 cách

- Trường hợp 3: Chọn 3 bi đỏ và 1 bi xanh có $C_{5}^{3} . C_{4}^{1}$ = 40 cách

- Trường hợp 4: Chọn 2 bi đỏ, 1 bi vàng và 1 bi xanh có $C_{5}^{2} . C_{3}^{1} . C_{4}^{1}$ = 120 cách

⇒n(D) = 20 + 60 + 40 + 120 = 240

Vậy P(D) = $\frac{n (D)}{n (Ω)}$ = $\frac{240}{495}$ = $\frac{16}{33}$

Câu 14. Cho tập hợp A = {2; 3; 4; 5; 6; 7; 8}. Gọi S là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được lập thành từ cách chữ số của tập A. Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn mà trong mỗi số luôn có mặt hai chữ số chẵn và hai chữ số lẻ.

A. $\frac{1}{5}$ ;

B. $\frac{3}{35}$ ;

C. $\frac{17}{35}$ ;

D. $\frac{18}{35}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: n(Ω) = $A_{7}^{4}$ = 840

Gọi E là biến cố: “ Số được chọn luôn có mặt hai chữ số chẵn và hai chữ số lẻ”

Việc số được chọn luôn có mặt hai chữ số chẵn và hai chữ số lẻ là một công việc gồm 3 công đoạn:

+ Công đoạn 1: Chọn 2 chữ số chẵn từ các chữ số 2; 4; 6; 8 có $C_{4}^{2}$ = 6 cách

+ Công đoạn 2: Chọn 2 chữ số lẻ từ các chữ số 3; 5; 7 có $C_{3}^{2}$ = 3 cách

+ Công đoạn 3: Từ 4 chữ số được chọn ta lập số có 4 chữ số khác nhau, số cách lập tương ứng với một hoán vị của 4 , do đó ta có 4! = 24 cách

⇒ n(E) = 24.6.3 = 432

⇒P(E) = $\frac{n (E)}{n (Ω)}$ = $\frac{432}{840}$ = $\frac{18}{35}$

Câu 15. Một Chi Đoàn có 3 Đoàn viên nữ và một số Đoàn viên nam.Cần lập một đội thanh niên tình nguyện (TNTN) gồm 4 người. Gọi A là biến cố:” 4 người được chọn có 3 nữ” và B là biến cố:” 4 người được chọn toàn nam”. Biết rằng P(A) = $\frac{2}{5}$ P(B). Hỏi Chi Đoàn có bao nhiêu Đoàn viên?

A. 9;

B. 10;

C. 11;

D. 12.

Hiển thị đáp án

Đáp án: A

Giải thích:

Gọi số Đoàn viên trong Chi đoàn là n (n ∈ℕ^*, n ≥ 7)

⇒Số Đoàn viên nam trong Chi Đoàn là n – 3

Ta có : Mỗi lần chọn 4 Đoàn viên ngẫu nhiên từ n Đoàn viên cho ta một tổ hợp chập 4 của n nên n(Ω) = $C_{n}^{4}$

* Để lập đội TNTN trong đó có 3 nữ có thể xem là một công việc gồm 2 công đoạn:

+ Công đoạn 1: Chọn 3 nữ có 1 cách chọn