Khi nào thì AM + MB = AB? Với ba điểm phân biệt A, B, M, ta có ba đoạn thẳng MA, MB, AB và MA + MB ≥ AB
Lời giải Tìm tòi và mở rộng trang 88 Toán 6 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 6.
Tìm tòi và mở rộng trang 88 Toán lớp 6 Tập 2:
Khi nào thì AM + MB = AB?
Với ba điểm phân biệt A, B, M, ta có ba đoạn thẳng MA, MB, AB và MA + MB ≥ AB.
- Nếu M nằm giữa hai điểm A và B (tức là M thuộc đoạn thẳng AB) thì MA + MB = AB. Ngược lại, nếu MA + MB = AB thì điểm M nằm giữa hai điểm A và B (Hình 52).
- Nếu M không nằm giữa hai điểm A và B (tức là M không thuộc đoạn thẳng AB) thì MA + MB > AB. Ngược lại, nếu MA + MB > AB thì điểm M không nằm giữa hai điểm A và B.
Áp dụng. Bạn Bình đi từ nhà đến trường theo một đường thẳng. Trên đường đến trường, bạn Bình lần lượt đi qua nhà bạn Cường và nhà bạn Long. Khoảng cách từ nhà bạn Bình đến nhà bạn Cường là 200 m, khoảng cách từ nhà bạn Cường đến nhà bạn Long là 300 m. Khoảng cách từ nhà bạn Bình đến trường là 1 200 m. Nhà bạn Cường và nhà bạn Long cách trường bao nhiêu mét?
Lời giải:
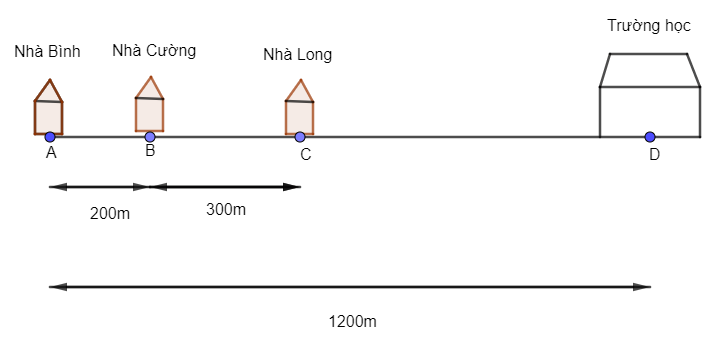
Đặt điểm A là vị trí nhà Bình, B là vị trí nhà Cường, C là vị trí nhà Long, D là vị trí trường học.
Do quãng đường từ nhà Bình đến trường lần lượt đi qua nhà bạn Cường và nhà bạn Long nên điểm B nằm giữa điểm A và điểm C. Khi đó, ta có:
AB + BC = AC
200 + 300 = AC
AC = 500.
Vì B nằm giữa A và D nên ta có AB + BD = AD
Mà AB = 200, AD = 1 200
Suy ra 200 + BD = 1 200
BD = 1 200 – 200
BD = 1 000.
Suy ra quãng đường từ nhà Cường đến trường là 1 000 m.
Ta lại có C nằm giữa A và D nên AC + CD = AD.
Mà AC = 500 m, AD = 1 200 m.
Suy ra 500 + CD = 1 200
CD = 1 200 – 500
CD = 700 m.
Suy ra quãng đường từ nhà Long đến trường là 700 m.
Vậy quãng đường từ nhà Cường đến trường là 1 000 m và quãng đường từ nhà Long đến trường là 700 m.
Xem thêm các bài giải sách giáo khoa Toán lớp 6 bộ sách Cánh Diều hay, chi tiết khác:
Hoạt động 2 trang 85 Toán lớp 6 Tập 2: Thực hiện theo các bước sau ( Hình 42): Bước 1. Vẽ đoạn thẳng AB, đường thẳng d và điểm C nằm trên d...
Hoạt động 5 trang 86 Toán lớp 6 Tập 2: Quan sát Hình 44. a) Hãy đo độ dài của các đoạn thẳng trong Hình 44. b) So sánh độ dài của hai đoạn thẳng AB và CD; AB và EG...
Luyện tập 3 trang 87 Toán lớp 6 Tập 2:...
Bài 3 trang 88 Toán lớp 6 Tập 2: Phát biểu đầy đủ các khẳng định sau đây: a) Nếu điểm C là trung điểm của đoạn thẳng PQ thì điểm 
nằm giữa hai điểm 
hai đoạn thẳng bằng nhau...
