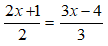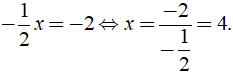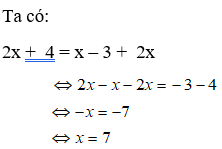Trắc nghiệm Toán học 8 Mở đầu về phương trình có đáp án năm 2021 - 2022
Bộ câu hỏi trắc nghiệm Toán học lớp 8 có đáp án, chọn lọc năm 2021 – 2022 mới nhất gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao. Hy vọng với tài liệu trắc nghiệm Toán học lớp 8 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 8
Trắc nghiệm Toán học 8 Mở đầu về phương trình
Bài 1: Tìm tập nghiệm của phương trình:
A. S = {11} B. S = {-11}
C. S = ∅ D. S = {0}
Chọn đáp án
Bài 2: Nghiệm x = - 4 là nghiệm của phương trình ?
A. - 2,5x + 1 = 11.
B. - 2,5x = - 10
C. 3x - 8 = 0
D. 3x - 1 = x + 7
+ Đáp án A: - 2,5x + 1 = 11 ⇔ - 2,5x = 10 ⇔ x = 10/ - 2,5 = - 4 → Đáp án A đúng.
+ Đáp án B: - 2,5x = - 10 ⇔ x = (-10)/(-0,25) = 4 → Đáp án B sai.
+ Đáp án C: 3x - 8 = 0 ⇔ 3x = 8 ⇔ x = 8/3 → Đáp án C sai.
+ Đáp án D: 3x - 1 = x + 7 ⇔ 3x - x = 7 + 1 ⇔ 2x = 8 ⇔ x = 4 → Đáp án D sai.
Chọn đáp án A.
Bài 3: Trong các phương trình sau, cặp phương trình nào tương đương?
A. x = 1 và x( x - 1 ) = 0
B. x - 2 = 0 và 2x - 4 = 0
C. 5x = 0 và 2x - 1 = 0
D. x2 - 4 = 0 và 2x - 2 = 0
Hai phương trình tương đương nếu chúng có cùng một tập hợp nghiệm.
Đáp án A:
+ Phương trình x = 1 có tập nghiệm S = { 1 }
+ Phương trình x( x - 1 ) = 0 ⇔ có tập nghiệm là S = { 0;1 }
→ Hai phương trình không tương đương.
Đáp án B:
+ Phương trình x - 2 = 0 có tập nghiệm S = { 2 }
+ Phương trình 2x - 4 = 0 có tập nghiệm là S = { 2 }
→ Hai phương trình tương đương.
Đáp án C:
+ Phương trình 5x = 0 có tập nghiệm là S = { 0 }
+ Phương trình 2x - 1 = 0 có tập nghiệm là S = { 1/2 }
→ Hai phương trình không tương đương.
Đáp án D:
+ Phương trình x2 - 4 = 0 ⇔ x = ± 2 có tập nghiệm là S = { ± 2 }
+ Phương trình 2x - 2 = 0 có tập nghiệm là S = { 1 }
→ Hai phương trình không tương đương.
Chọn đáp án B.
Bài 4: Tập nghiệm của phương trình 3x - 6 = 0 là ?
A. S = { 1 }
B. S = { 2 }
C. S = { - 2 }
D. S = { 1 }
Ta có: 3x - 6 = 0 ⇔ 3x = 6 ⇔ x = 2
→ Phương trình có tập nghiệm là S = { 2 }
Chọn đáp án B.
Bài 5: Phương trình - 1/2x = - 2 có nghiệm là ?
A. x = - 2. B. x = - 4.
C. x = 4. D. x = 2.
Ta có:
Vậy phương trình có tập nghiệm là x = 4.
Chọn đáp án C.
Bài 6: Giải phương trình: (2x + 4).(4 - x) = 0
A. S = {-2; 4} B. S = {2; 4}
C. S = {2; - 4} D. S = {-2; - 4}
Ta có: (2x + 4).(4 - x) = 0 khi và chỉ khi:
(2x + 4) = 0 hoặc 4 – x = 0
* 2x + 4 = 0 khi x = -2
* 4 – x = 0 khi x = 4
Vậy tập nghiệm của phương trình là: S = {-2; 4}.
Chọn đáp án A
Bài 7: Hỏi x = 3 là nghiệm của phương trình nào?
A. 2x + 6 = 0 B. 6 – 2x = 0
C. 3 + x = 0 D. 3x + 1 = 0
Xét phương án B: Với x = 3 thì
VT = 6 - 2x = 6 – 2.3 = 0 = VP
Do đó, x = 3 là nghiệm của phương trình 6 – 2x = 0
Chọn đáp án B
Bài 8: Phương trình 2x + 4 = x – 3 + 2x tương đương với phương trình nào sau đây ?
A. –x = 7 B. 2x + 4 = 0
C. –x = - 7 D. 2x – 4 = 0
Chọn đáp án
Bài 9: Phương trình x2 + 2x + 2 = (x - 2)2 có mấy nghiệm
A. 0 B. 1
C. 2 D. 3
Chọn đáp án
Bài 10: Trong các phương trình sau, phương trình nào là phương trình một ẩn?
A. 2x = x + 1.
B. x + y = 3x.
C. 2a + b = 1.
D. xyz = xy.
+ Một phương trình với ẩn x là hệ thức có dạng A( x ) = B( x ), trong đó A( x ) gọi là vế trái, B( x ) gọi là vế phải.
+ Nghiệm của phương trình là giá trị của ẩn x thoả mãn (hay nghiệm đúng) phương trình.
Nhận xét:
+ Đáp án A: là phương trình một ẩn là x
+ Đáp án B: là phương trình hai ẩn là x,y
+ Đáp án C: là phương trình hai ẩn là a,b
+ Đáp án D: là phương trình ba ẩn là x,y,z
Chọn đáp án A.
Bài viết liên quan
- Trắc nghiệm Toán học 8 Diện tích hình thang có đáp án năm 2021 - 2022
- Trắc nghiệm Toán học 8 Diện tích hình thoi có đáp án năm 2021 - 2022
- Trắc nghiệm Toán học 8 Phương trình bậc nhất một ẩn có đáp án năm 2021 - 2022
- Trắc nghiệm Toán học 8 Phương trình đưa được về dạng ax + b = 0 có đáp án năm 2021 - 2022
- Trắc nghiệm Toán học 8 Phương trình tích có đáp án năm 2021 - 2022
