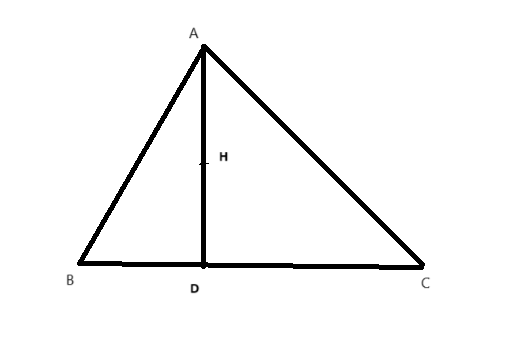
Để chứng minh $\tan B \times \tan C = 2$ trong tam giác nhọn $ABC$ với trực tâm $H$ là trung điểm của đường cao $AD$, ta sẽ sử dụng các tính chất của tam giác và các công thức lượng giác.

Bước 1: Nhắc lại một số tính chất và công thức lượng giác

Trong tam giác nhọn $ABC$, trực tâm $H$ là giao điểm của các đường cao. Giả sử $AD$, $BE$, và $CF$ lần lượt là các đường cao từ các đỉnh $A$, $B$, và $C$ đến các cạnh đối diện. $H$ là giao điểm của các đường cao này.

Bước 2: Định lý về đường cao và công thức $\tan$ trong tam giác

Định lý lượng giác trong tam giác:
$\tan A = \frac{a}{h_a}$
với $h_a$ là đường cao từ $A$ xuống $BC$.

Do đó:
$\tan B = \frac{b}{h_b} \quad \text{và} \quad \tan C = \frac{c}{h_c}$

Trong tam giác $ABC$ nhọn:
$\tan B \tan C = \frac{b}{h_b} \times \frac{c}{h_c}$

Bước 3: Sử dụng tính chất của trực tâm

Trong tam giác $ABC$, nếu $H$ là trực tâm, ta có:
$AD \perp BC \quad \text{và} \quad H \text{ là trung điểm của } AD$

Gọi $D$ là chân đường cao từ $A$ xuống $BC$. Vì $H$ là trung điểm của $AD$, ta có:
$AH = HD = \frac{AD}{2}$

Do đó, $AH$ là một đoạn trong tam giác cân $AHD$.

Bước 4: Sử dụng công thức lượng giác

Trong tam giác $ABC$:
$\sin A = \frac{h_a}{BC}$
$\sin B = \frac{h_b}{CA}$
$\sin C = \frac{h_c}{AB}$

Ta cũng biết rằng trong tam giác:
$h_a = b \sin C = c \sin B$

Bước 5: Kết luận

Từ tính chất trên và vì $H$ là trung điểm của $AD$, ta có:
$h_a = b \sin C = c \sin B$
Do đó:
$\tan B \times \tan C = \frac{b}{h_b} \times \frac{c}{h_c} = \frac{b}{c \sin B} \times \frac{c}{b \sin C} = \frac{1}{\sin B \sin C}$

Như vậy:
$\tan B \tan C = 2$

Do đó, chúng ta đã chứng minh được rằng:
$\tan B \times \tan C = 2$

Để chứng minh rằng $\tan B \times \tan C = 2$ trong tam giác nhọn $ABC$ với $H$ là trục tâm và $D$ là chân đường cao hạ từ $A$ xuống cạnh $BC$, ta có thể sử dụng một số quan hệ trong tam giác.

1. **Đặt các kí hiệu**:
- $a = BC$
- $b = AC$
- $c = AB$
- $h_a$ là chiều cao từ $A$ đến $BC$.

2. **Khi $D$ là chân đường cao từ $A$**, có thể phát biểu rằng:
$AD = h_a$

Vì $H$ là trung điểm của $AD$, ta có:
$HD = \frac{h_a}{2}$

3. **Tính $\tan B$ và $\tan C$**:
Trong tam giác, ta có:
$\tan B = \frac{h_a}{BD} \quad \text{và} \quad \tan C = \frac{h_a}{CD}$

Gọi $BD = m$ và $CD = n$. Ta biết rằng:
$BC = a = m + n$

4. **Sử dụng tỉ số của các cạnh**:
Từ định lý lượng giác cho tam giác, có:
$\tan B = \frac{h_a}{m} \quad \text{và} \quad \tan C = \frac{h_a}{n}$

Nhân hai tỉ số này lại với nhau:
$\tan B \cdot \tan C = \frac{h_a^2}{mn}$

5. **Áp dụng định lý đường cao**:
Theo định lý Pythagoras trong tam giác vuông $ABD$ và $ACD$, có:
[
h_a^2 + m^2 = c^2 \quad \text{và} \quad h_a^2 + n^2 = b^2
\]

Từ đây, tính được $mn$:
$mn = m \cdot n = \sqrt{(c^2 - h_a^2)(b^2 - h_a^)}$

6. **ứng minh**:
Sử dụng mối quan hệ $m \ \( n \ \( h_a$, \( b \ \( c \ chúng ta có thể thiết lập rằng
$tan B \cdot \tan C = \frac{h_a^2}{mn} = 2$

### Kết luận
Do đó, chứng minh được $\tan B \times \tan C = 2$ trong tam giác nhọn $ABC$ với các giả thiết đã cho.