Cho đa thức F(x) = x^4 − x^3 − 6x^2 + 15x − 9
Lời giải Bài 9 trang 70 SBT Toán 7 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 9 trang 70 SBT Toán 7 Tập 2:
Cho đa thức F(x) = x4 − x3 − 6x2 + 15x − 9.
a) Kiểm tra lại rằng x = 1 và x = −3 là hai nghiệm của F(x).
b) Tìm đa thức G(x) sao cho F(x) = (x − 1)(x + 3) . G(x)
Lời giải:
a) Ta có : F(1) = 14 − 13 – 6 . 12 + 15 . 1 − 9
= 1 − 1 − 6 + 15 − 9 = 0.
F(−3) = (−3)4 − (−3)3 – 6 . (−3)2 + 15 . (−3) − 9
= 81 + 27 − 6.9 + 15. (−3) − 9
= 81 + 27 − 54 − 45 − 9 = 0.
Vậy x = 1 và x = −3 là hai nghiệm của F(x).
b) Ta có G(x) = F(x) : [(x − 1)(x + 3)]
= F(x) : [ x(x +3) – 1 . (x + 3)]
= F(x) : (x2 + 3x − x − 3)
= F(x) : (x2 +2x − 3)
Ta đặt tính chia :
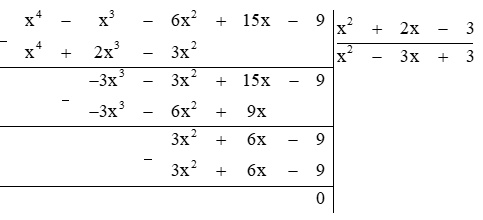
Vậy G(x) = x2 − 3x + 3.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:
Bài 2 trang 69 SBT Toán 7 Tập 2: Tính giá trị của biểu thức sau...
Bài 3 trang 69 SBT Toán 7 Tập 2: Bạn Minh đọc một cuốn sách trong ba ngày thì xong. Ngày thứ nhất, Minh đọc được số trang sách. Ngày thứ hai, Minh đọc được số trang sách còn lại. Ngày thứ ba, Minh đọc nốt 36 trang còn lại. Hỏi cuốn sách bạn Minh đọc có bao nhiêu trang?...
Bài 4 trang 69 SBT Toán 7 Tập 2: a) Không dùng máy tính, hãy tính . b) Trong hai số 1,7(3) và , số nào lớn hơn?...
Bài 5 trang 69 SBT Toán 7 Tập 2: a) Trên trục số, hãy xác định điểm biểu diễn số . b) Viết biểu thức dưới dạng không chứa dấu giá trị tuyệt đối...
Bài 6 trang 69 SBT Toán 7 Tập 2: Trong một đợt phát động làm kế hoạch nhỏ, ba lớp 7A, 7B, 7C tham gia thu gom giấy vụn. Số kilôgam giấy vụn gom được của ba lớp này lần lượt tỉ lệ với 2; 4; 5...
Bài 7 trang 69 SBT Toán 7 Tập 2: Xe ô tô và xe máy cùng đi từ tỉnh A đến tỉnh B trên cùng một con đường. Biết rằng xe ô tô đi với vận tốc 80 km/h, xe máy đi với vận tốc 60 km/h...
Bài 8 trang 69 SBT Toán 7 Tập 2: Hai đa thức A(x) và B(x) thỏa mãn: A(x) + B(x) = x3 − 5x2 − 2x + 4 và A(x) − B(x) = − x3 + 3x2 − 2...
Bài 9 trang 70 SBT Toán 7 Tập 2: Cho đa thức F(x) = x4 − x3 − 6x2 + 15x − 9. a) Kiểm tra lại rằng x = 1 và x = −3 là hai nghiệm của F(x)...
Bài 10 trang 70 SBT Toán 7 Tập 2: Tính góc Mby trong Hình 1, biết rằng Ax // By. HD. Kẻ thêm đường thẳng đi qua M và song song với Ax...
Bài 12 trang 70 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại đỉnh A; ba điểm M, N, P lần lượt nằm trên các cạnh BC, CA, AB của tam giác ABC sao cho M là trung điểm của BC, MN vuông góc với AC và MP vuông góc với AB. Chứng minh rằng...
Bài 13 trang 70 SBT Toán 7 Tập 2: Cho bốn điểm A, B, C và D như Hình 2. Biết rằng , và AB = DC. Chứng minh rằng...
Bài 14 trang 70 SBT Toán 7 Tập 2: Tròn đưa cho Vuông một tờ giấy, trên đó có vẽ điểm C và hai đường thẳng a và b không đi qua C, cho biết hai đường thẳng a và b không song song với nhau (giao điểm của a và b nằm ngoài tờ giấy)...
Bài 15 trang 71 SBT Toán 7 Tập 2: a) Chứng minh rằng nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại đỉnh A...
Bài 16 trang 71 SBT Toán 7 Tập 2: Cho hai biểu đồ sau biểu diễn các số liệu tại một trường Trung học cơ sở...
Bài 17 trang 71 SBT Toán 7 Tập 2: Một nhà mạng muốn tìm hiểu loại nhạc chuông của điện thoại di động được người dùng yêu thích, đã lập phiếu khảo sát như hình bên và dự kiến tiến hành thu thập dữ liệu theo hai cách sau...
Bài 18 trang 71 SBT Toán 7 Tập 2: Cho một hộp đựng n viên bi màu xanh và m viên bi màu đỏ. Lấy ngẫu nhiên một viên bi trong hộp...


