Cho góc xOy khác góc bẹt. Oz là tia phân giác của góc đó, M là một điểm bất kì thuộc tia Oz
Lời giải Bài 68 trang 88 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 68 trang 88 SBT Toán 7 Tập 2: Cho góc xOy khác góc bẹt. Oz là tia phân giác của góc đó, M là một điểm bất kì thuộc tia Oz. Qua M vẽ đường thẳng a vuông góc với Ox tại A, cắt Oy tại C. Qua M vẽ đường thẳng b vuông góc với Oy tại B, cắt Ox tại D. Chứng minh:
a) OM là đường trung trực của đoạn thẳng AB;
b) Tam giác DMC là tam giác cân.
Lời giải
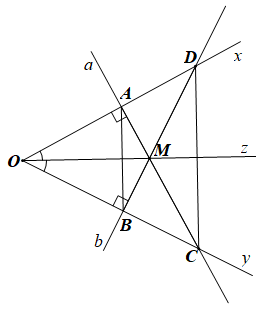
a) Vì Oz là tia phân giác của góc xOy nên .
Xét OAM và OBM có
,
OM là cạnh chung,
(do )
Do đó ∆OAM = ∆OBM (cạnh huyền – góc nhọn).
Suy ra OA = OB và MA = MB (các cặp cạnh tương ứng).
Nên O và M cùng nằm trên đường trung trực của AB.
Vậy OM là đường trung trực của AB.
b) Xét ADM và BCM có
,
AM = BM (chứng minh câu a),
(hai góc đối đỉnh)
Do đó ∆ADM = ∆BCM (cạnh huyền – góc nhọn).
Suy ra MD = MC (hai cạnh tương ứng).
Do đó tam giác CDM cân tại M.
Vậy tam giác DMC cân tại M.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài 60 trang 87 SBT Toán 7 Tập 2: Xác định điểm M thuộc đường thẳng BC sao cho M cách đều A và B trong mỗi trường hợp sau: a) Tam giác nhọn ABC...
Bài 64 trang 87 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A có . Đường trung trực của BC cắt AC tại M. Chứng minh: a) BM là tia phân giác của góc ABC...
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
