Trắc nghiệm Toán 7 Bài 6: Tính chất ba đường trung trực của tam giác
Bộ 15 bài tập trắc nghiệm Toán 7 Bài 6: Tính chất ba đường trung trực của tam giác có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 6.
Trắc nghiệm Toán 7 Bài 6: Tính chất ba đường trung trực của tam giác - Chân trời sáng tạo
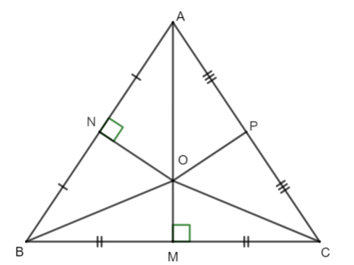
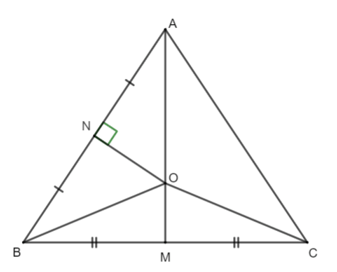
Câu 1. Cho ∆ABC, P là trung điểm của AC. Các đường trung trực của AB và BC cắt nhau tại O. Số đo bằng:
A. 30°;
B. 60°;
C. 90°;
D. 45°.
Đáp án: C
Giải thích:
Gọi M và N lần lượt là trung điểm của BC và AC.
Xét ∆ABC ta có:
ON là đường trung trực của AB;
OM là đường trung trực của BC;
ON và OM cắt nhau tại O.
Do đó O cách đểu ba đỉnh của ∆ABC.
Suy ra OA = OB = OC.
Xét ∆OPA và ∆OPC có:
OP là cạnh chung;
OA = OC (cmt);
PA = PC (P là trung điểm của AC).
Do đó ∆OPA = ∆OPC (c.c.c).
Suy ra = (hai góc tương ứng)
Mà + = 180° nên = = 90°.
Vậy số đo góc bằng 90°.
Câu 2. Điền vào chỗ trống sau: “Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này … ba đỉnh của tam giác đó.”
A. Giao;
B. Nằm trên;
C. Cách đều;
D. Thuộc.
Đáp án: C
Giải thích:
Câu 3. Cho tam giác ABC có M và N lần lượt là trung điểm của AB, BC. Từ M, N vẽ hai đường trung trực cắt nhau tại O. Cho OA= 5 cm. Độ dài đoạn thẳng OB bằng:
A. 4 cm;
B. 5 cm;
C. 10 cm;
D. 20 cm.
Đáp án: B
Giải thích:
Xét ∆ABC có:
OM là đường trung trực của AB (gt);
ON là đường trung trực của BC (gt);
OM và ON cắt nhau tại O.
Do đó O cách đều ba đỉnh của ∆ABC.
Suy ra OA = OB = 5 (cm).
Vậy độ dài đoạn thẳng OB bằng 5 cm.
Câu 4. Gọi O là giao điểm của ba đường trung trực trong ∆ABC. Khi đó điểm O là:
A. Trọng tâm của ∆ABC;
B. Điểm cách đều ba cạnh của ∆ABC;
C. Điểm cách đều ba đỉnh của ∆ABC;
D. Tất cả các đáp án trên đều sai.
Đáp án: C
Giải thích:
Theo định lí: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
Do đó O là điểm cách đều ba đỉnh của ∆ABC.
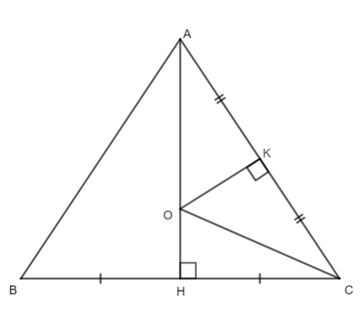
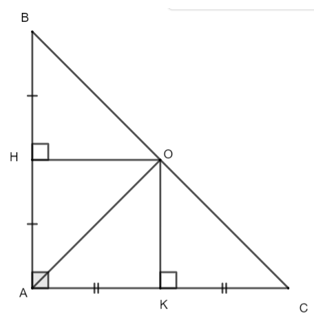
Câu 5. Cho tam giác ABC cân tại A có góc = 60° có AH là đường cao và K là trung điểm của AC. Từ K kẻ đường trung trực của AC cắt AH tại O. Số đo góc OCA là:
A. 30°;
B. 45°;
C. 60°;
D. 90°.
Đáp án: A
Giải thích:
Xét ∆ABH và ∆ACH cùng vuông tại H có:
AH là cạnh chung;
AB = AC (∆ABC cân tại A).
Do đó ∆ABH = ∆ACH (cạnh huyền - cạnh góc vuông)
Suy ra HB = HC
Ta có: AH ⊥ BC tại H;
H là trung điểm của BC (HB = HC).
Suy ra AH là đường trung trực của cạnh BC.
Ta có: AH là đường trung trực của cạnh BC (cmt);
OK là đường trung trực của cạnh AC (gt);
AH cắt OK tại O.
Do đó O cách đều ba đỉnh của ∆ABC.
Suy ra OA = OC.
Nên ∆OAC cân tại O.
Ta có: = (∆ABH = ∆ACH, hai góc tương ứng);
= 60°.
Suy ra = 60°.
Do đó = 60° : 2 = 30°.
Ta có: = (∆OAC cân tại O).
= 30° (cmt).
Do đó = 30°.
Vậy số đo góc bằng 30°.
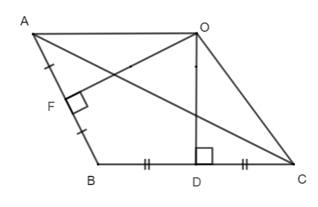
Câu 6. Quan sát hình bên dưới, cho biết OA = 8cm. Độ dài đoạn thẳng OC bằng:
A. 8;
B. 16;
C. 4;
D. 2.
Đáp án: A
Giải thích:
Xét ∆ABC có:
OF là đường trung trực của AB (hình vẽ);
OD là đường trung trực của BC (hình vẽ);
OF và OD cắt nhau tại O.
Do đó O cách đều ba đỉnh của ∆ABC.
Suy ra OA = OC = 8 (cm).
Vậy độ dài đoạn thẳng OC = 8 cm.
Câu 7. Cho tam giác ∆ABC vuông cân tại A có H và K lần lượt là trung điểm của hai cạnh AB và AC. Từ H và K kẻ đường trung trực của hai cạnh AB và AC cắt nhau tại O. Tính số đo .
A. 30°;
B. 45°;
C. 60°;
D. 90°.
Đáp án: B
Giải thích:
Xét ∆ABC ta có:
OH là đường trung trực của AB (gt);
OK là đường trung trực của AC (gt);
OH và OK cắt nhau tại O.
Do đó O cách đều ba đỉnh của ∆ABC.
Suy ra OA = OB = OC
Xét ∆OBA và ∆OCA ta có:
OA là cạnh chung;
OB = OC (cmt);
AB = AC (∆ABC cân tại A).
Suy ra ∆OBA = ∆OCA (c.c.c)
Do đó = (hai góc tương ứng )
Ta có: = (cmt);
+ = = 90°.
Suy ra = 90° : 2 = 45°
Vậy số đo bằng 45°.
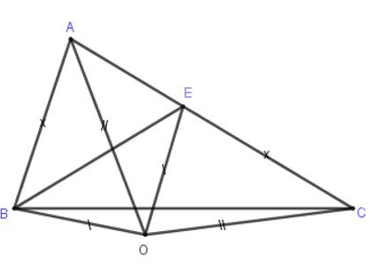
Câu 8. Cho tam giác ∆ABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Các đường trung trực của BE và AC cắt nhau tại O. Chọn câu đúng:
A. ∆AOB = ∆COE;
B. ∆ABO = ∆CEO;
C. ∆ABE = ∆CDE;
D. ∆ABO = ∆COE.
Đáp án: A
Giải thích:
Xét ∆AOB và ∆COE có
OA = OC (vì O thuộc đường trung trực của AC);
OB = OE (vì O thuộc đường trung trực của BE);
AB = CE (gt).
Suy ra ∆AOB = ∆COE (c.c.c).
Vậy đáp án đúng là câu A.
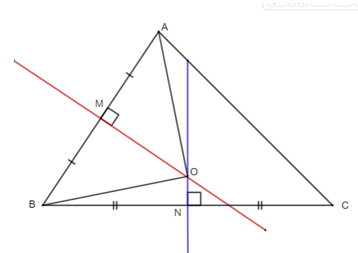
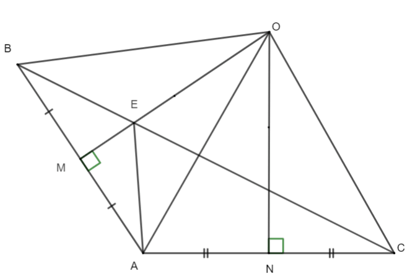
Câu 9. Cho tam giác ∆ABC có là góc tù. Các đường trung trực của AB và AC cắt nhau tại O và đường trung trực của AB cắt BC tại E. Khi đó, ∆EAB là:
A.Tam giác thường;
B. Tam giác vuông;
C. Tam giác đều;
D. Tam giác cân.
Đáp án: D
Giải thích:
Gọi M và N lần lượt là trung điểm của AB và AC.
Ta có: E nằm trên đường trung trực của AB.
Suy ra E cách đều 2 đầu mút của đoạn thẳng AB.
Do đó EA = EB.
Vậy ∆EAB là tam giác cân tại E.
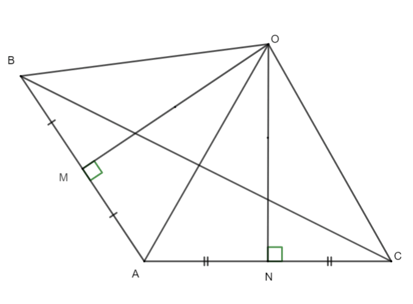
Câu 10. Cho tam giác ∆ABC có là góc tù. Các đường trung trực của AB và AC cắt nhau tại O. Đường tròn tâm O bán kính OA đi qua điểm:
A. B và C;
B. M và N;
C. B;
D. C.
Đáp án: A
Giải thích:
Gọi M và N lần lượt là trung điểm của AB và AC.
Xét ∆ABC có:
OM là đường trung trực của AB;
ON là đường trung trực của AC;
OM và ON cắt nhau tại O.
Suy ra O cách đều ba đỉnh ∆ABC.
Do đó OA = OB = OC
Vậy đường tròn tâm O bán kính OA đi qua các điểm B và C.
Câu 11. Cho tam giác ∆ABC cân tại A, có M là trung điểm của BC. Đường trung trực của AB cắt AM tại O. Khi đó điểm O:
A. Là trọng tâm của ∆ABC;
B. Cách đều ba cạnh của ∆ABC;
C. Là trực tâm của ∆ABC;
D. Cách đều ba đỉnh của ∆ABC.
Đáp án: D
Giải thích:
Gọi N là trung điểm của AB.
Do đó N thuộc đường trung trực của AB.
Xét ∆ABM và ∆ACM ta có:
AM là cạnh chung;
AB = AC (∆ABC cân tại A);
MB = MC (M là trung điểm của BC).
Do đó ∆ABM = ∆ACM (c.c.c).
Suy ra = (hai góc tương ứng)
Mà + = 180 nên = = 90
Vì thế AM vuông góc với BC tại M.
Ta có: AM vuông góc với BC tại M;
M là trung điểm của BC.
Suy ra AM là đường trung trực của BC.
Xét ∆ABC có: AM là đường trung trực của BC (cmt);
ON là đường trung trực của AB.
AM cắt ON tại O (gt).
Vậy O cách đều ba đỉnh của ∆ABC.
Câu 12. Điền vào chỗ trống sau: “Trong một tam giác, đường trung trực của mỗi cạnh gọi là … của tam giác đó”.
A. Đường trung tuyến;
B. Đường trung trực;
C. Trọng tâm;
D. Trung điểm.
Đáp án: B
Giải thích:
Câu 13. Cho tam giác ∆ABC có M và N lần lượt là trung điểm của AB, BC. Từ M và N vẽ 2 đường trung trực cắt nhau tại O. Biết đường tròn tâm O bán kính OA có đường kính bằng 8 cm. Độ dài đoạn thẳng OB bằng:
A. 2 cm;
B. 4 cm;
C. 8 cm;
D. 5 cm.
Đáp án: B
Giải thích:
Xét ∆ABC có:
OM là đường trung trực của AB (gt);
ON là đường trung trực của BC (gt);
OM và ON cắt nhau tại O.
Do đó O cách đều ba đỉnh của ∆ABC.
Suy ra OA = OB = OC.
Ta có: Đường tròn tâm O bán kính OA có đường kính bằng 8 cm.
Suy ra: OA = 4 (cm).
Mà OA = OB (cmt).
Nên OB = 4 (cm).
Vậy độ dài đoạn thẳng OB bằng 4 cm.
Câu 14. Một điểm được gọi là cách đều ba đỉnh của một tam giác khi là:
A. Giao điểm của ba đường cao của tam giác;
B. Giao điểm của ba đường trung trực của tam giác;
C. Trọng tâm của tam giác;
D. Trực tâm của tam giác.
Đáp án: B
Giải thích:
Câu 15. Giao điểm O của ba đường trung trực của tam giác thuộc:
A. Đường tròn tâm O đi qua ba đỉnh của tam giác;
B. Đường tròn tâm O nằm trong tam giác;
C. Đường tròn tâm O đi qua ba cạnh của tam giác;
D. Đường tròn tâm O đi qua một đỉnh của tam giác.
Đáp án: A
Giải thích:
Gọi ∆ABC có O là giao điểm của ba đường trung trực.
Suy ra O cách đều ba đỉnh của ∆ABC.
Nên OA = OB = OC.
Vậy đường tròn tâm O đi qua ba đỉnh của tam giác.
Các câu hỏi trắc nghiệm Toán 7 sách Chân trời sáng tạo có đáp án, chọn lọc khác: