Trắc nghiệm Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến
Bộ 15 bài tập trắc nghiệm Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 3.
Trắc nghiệm Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo
Câu 1. Rút gọn biểu thức B(x) = (1 − 5x) + [(4 − 9x2) + (10x − 7)], ta được biểu thức nào trong các biểu thức sau đây?
A. 5x − 2;
B. 9x2 + 5x − 2;
C. −9x2 + 15x + 12;
D. −9x2 + 5x − 2.
Đáp án: D
Giải thích:
Ta có: B(x) = (1 − 5x) + [(4 − 9x2) + (10x − 7)]
= 1 − 5x + 4 − 9x2 + 10x − 7
= − 9x2 + (−5x + 10x) + (1 + 4 − 7)
= −9x2 + 5x – 2.
Vậy B(x) = −9x2 + 5x – 2.
Câu 2. Cho hai đa thức A(x) = x2 − 5x + 7 và B(x) = 3x2 − 2x + 10. Tính A(x) + B(x).
A. 3x2 − 2x + 10;
B. 3x2 − 2x + 10;
C. 4x2 − 7x + 17;
D. −2x2 − 3x + 10.
Đáp án: C
Giải thích:
Ta có: A(x) + B(x) = (x2 − 5x + 7) + (3x2 − 2x + 10)
= x2 − 5x + 7 + 3x2 − 2x + 10
= (x2 + 3x2) + (−5x − 2x) + (7 + 10)
= 4x2 − 7x + 17.
Vậy A(x) + B(x) = 4x2 − 7x + 17.
Câu 3. Cho hai đa thức P(x) = 6x3 − 3x2 − 2x + 4 và G(x) = 5x2 − 7x + 9. Tính P(x) − G(x).
A. x2 − 9x +13;
B. 6x3 − 8x2 + 5x −5;
C. x3 − 8x2 + 5x −5;
D. 5x3 − 8x2 + 5x +13.
Đáp án: B
Giải thích:
Ta có: P(x) − G(x) = (6x3 − 3x2 − 2x + 4) − (5x2 − 7x + 9)
= 6x3 − 3x2 − 2x + 4 − 5x2 + 7x − 9
= 6x3 + (−3x2 − 5x2) + (−2x + 7x) + (4 − 9)
= 6x3 − 8x2 + 5x −5.
Vậy P(x) − G(x) = 6x3 − 8x2 + 5x −5.
Câu 4. Cho đa thức U(x) = 7x2 + 4x − 3. Tìm đa thức V(x) sao cho U(x) + V(x) = x3 + x2 –5.
A. V(x) = x3 − 6x2 − 4x − 2;
B. V(x) = 6x2 − 4x − 2;
C. V(x) = x3 − 8x2 + 5x +13;
D. V(x) = x3 − 6x2 − 2.
Đáp án: A
Giải thích:
Ta có: U(x) = 7x2 + 4x − 3
Vì U(x) + V(x) = x3 + x2 −5 nên
V(x) = x3 + x2 − 5 − U(x)
= x3 + x2 − 5 − (7x2 + 4x − 3)
= x3 + x2 − 5 − 7x2 − 4x + 3
= x3 + (x2 − 7x2) − 4x + (−5 + 3)
= x3 − 6x2 − 4x – 2.
Vậy V(x) = x3 − 6x2 − 4x – 2.
Câu 5. Cho đa thức G(x) = 3x4 − 4x3 − 2x + 27. Tìm đa thức H(x) sao cho H(x) − G(x) = x3 − 5x2 + 10.
A. 3x4 − 3x3 − 5x2 + 2x + 37;
B. 3x4 + 3x3 − 5x2 − 2x + 37;
C. − 3x3 − 5x2 − 2x + 37;
D. 3x4 − 3x3 − 5x2 − 2x + 37.
Đáp án: D
Giải thích:
Ta có: G(x) = 3x4 − 4x3 − 2x + 27
Vì H(x) − G(x) = x3 − 5x2 + 10 nên:
H(x) = x3 − 5x2 + 10 + G(x)
= x3 − 5x2 + 10 + (3x4 − 4x3 − 2x + 27)
= x3 − 5x2 + 10 + 3x4 − 4x3 − 2x + 27
= 3x4 + (x3 − 4x3) − 5x2 − 2x + (10 + 27)
= 3x4 − 3x3 − 5x2 − 2x + 37.
Vậy H(x) = 3x4 − 3x3 − 5x2 − 2x + 37.
Câu 6. Cho đa thức M(x) = 4x3 − 2x + 17. Tìm đa thức N(x) sao cho M(x) − N(x) = − x4 − 4x2 + 1.
A.x4 + 4x3 + 4x2 − 2x +16;
B. −x4 + 4x3 + 4x2 − 2x +16;
C. −x4 − 4x3 + 4x2 − 2x +16;
D. x4 + 4x3 − 4x2 − 2x +16.
Đáp án: A
Giải thích:
Ta có: M(x) = 4x3 − 2x + 17
Vì M(x) − N(x) = − x4 − 4x2 + 1 nên
N(x) = M(x) − (− x4 − 4x2 + 1)
= 4x3 − 2x + 17 − (− x4 − 4x2 + 1)
= 4x3 − 2x + 17 + x4 + 4x2 − 1
= x4 + 4x3 + 4x2 − 2x + (17 − 1)
= x4 + 4x3 + 4x2 − 2x + 16
Vậy N(x) = x4 + 4x3 + 4x2 − 2x +16.
Câu 7. Cho ba đa thức A(x) = x2 − 3x +10; B(x) = 3x3 +16; C(x) = 2x4 − 4x2 − 8x.
Tính A(x) + B(x) + C(x).
A. 2x4 + 3x3 − 3x2 − 5x + 26;
B. 2x4 + 3x3 − 3x2 − 11x +26;
C. 2x4 + 3x3 + 7x2 − 11x +26;
D. x4 + 3x3 − 3x2 − 11x +26.
Đáp án: B
Giải thích:
Ta có: A(x) + B(x) = (x2 − 3x +10) + (3x3 +16)
= x2 − 3x +10 + 3x3 +16
= 3x3 + x2 − 3x +(10 +16)
= 3x3 + x2 − 3x + 26
Ta có: A(x) + B(x) + C(x) = (3x3 + x2 − 3x + 26) + (2x4 − 4x2 − 8x)
= 3x3 + x2 − 3x + 26 + 2x4 − 4x2 − 8x
= 2x4 + 3x3 + (x2 − 4x2) + (−3x − 8x) +26
= 2x4 + 3x3 − 3x2 − 11x +26.
Vậy A(x) + B(x) + C(x) = 2x4 + 3x3 − 3x2 − 11x +26.
Câu 8. Cho ba đa thức A(x) = x2 − 3x +10; B(x) = 3x3 +16; C(x) = 2x4 − 4x2 − 8x.
Tính A(x) − B(x) − C(x).
A. −2x4 − 3x3 + 5x2 + 5x − 6;
B. 2x4 + 3x3 − 3x2 − 11x +26;
C. −2x4 − 3x3 − 3x2 + 5x − 6;
D. −2x4 − 3x3 + 5x2 − 11x − 6.
Đáp án: A
Giải thích:
Ta có: A(x) − B(x) = (x2 − 3x +10) − (3x3 +16)
= x2 − 3x + 10 − 3x3 − 16
= − 3x3 + x2 − 3x + (10 − 16)
= − 3x3 + x2 − 3x – 6.
Khi đó: A(x) − B(x) − C(x)
= (−3x3 + x2 − 3x − 6) − (2x4 − 4x2 − 8x)
= −3x3 + x2 − 3x − 6 − 2x4 + 4x2 + 8x
= −2x4 − 3x3 + (x2 + 4x2) + (−3x + 8x) − 6
= −2x4 − 3x3 + 5x2 + 5x – 6.
Vậy A(x) − B(x) − C(x) = −2x4 − 3x3 + 5x2 + 5x – 6.
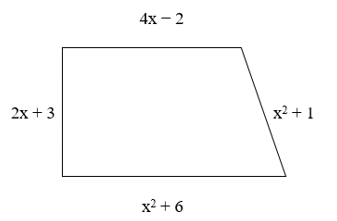
Câu 9. Biểu thức biểu thị chu vi của hình thang vuông như hình bên dưới là:
A. x2 + 6x + 4;
B. 2x2 − 6x + 8;
C. 2x2 + 2x + 8;
D. 2x2 + 6x + 8.
Đáp án: D
Giải thích:
Chu vi của hình thang bằng tổng độ dài hai cạnh đáy và hai cạnh bên. Khi đó:
P = (4x −2 + x2 + 6) + (2x + 3 + x2 + 1) (với P là chu vi của hình thang)
= 4x − 2 + x2 + 6 + 2x + 3 + x2 + 1
= (x2 + x2) + (4x + 2x)+ (−2 + 6 + 3 + 1)
= 2x2 + 6x +8.
Vậy chu vi của hình thang vuông trên được biểu thị bằng biểu thức 2x2 + 6x +8.
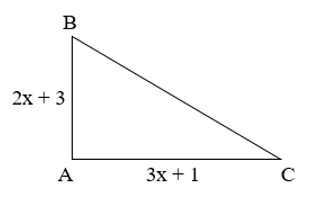
Câu 10. Cho tam giác vuông (như hình bên dưới) có chu vi bằng 14x – 4. Tính cạnh BC của tam giác ABC.
A. 9x − 8;
B. 9x + 8;
C. 7x − 8;
D. 9x + 4.
Đáp án: A
Giải thích:
Chu vi tam giác trên bằng tổng độ dài ba cạnh nên ta có:
P = AB + AC + BC (với P là chu vi của hình tam giác)
Suy ra BC = P − AB − AC
= 14x − 4 − (2x +3) − (3x+1)
= 14x − 4 − 2x − 3 − 3x − 1
= (14x − 2x − 3x) + (−4 − 3 − 1)
= 9x – 8.
Vậy BC = 9x – 8.
Câu 11. Rút gọn biểu thức A(x) = (2x2 + 1) + [(6x − 3) + (9 − 2x2)], ta được biểu thức nào trong các biểu thức sau đây?
A. A(x) = 6x + 7;
B. A(x) = 4x2 + 6x + 7;
C. A(x) = 6x + 12;
D. A(x) = 4x2 + 6x + 12.
Đáp án: A
Giải thích:
Ta có: A(x) = (2x2 + 1) + [(6x − 3) + (9 − 2x2)]
= 2x2 + 1 + 6x − 3 + 9 − 2x2
= (2x2 − 2x2) + 6x + (1 − 3 + 9)
= 6x + 7.
Vậy A(x) = 6x + 7.
Câu 12. Cho hai đa thức G(x) = 2x + 7 và H(x) = 3x +6. Tính G(x) + H(x).
A. −x + 1;
B. 5x + 13;
C. 5x + 1;
D. x − 1.
Đáp án: B
Giải thích:
Ta có: G(x) + H(x) = (2x + 7) + (3x +6)
= 2x + 7 + 3x +6 = (2x + 3x) + (6 + 7) = 5x + 13.
Vậy G(x) + H(x) = 5x + 13.
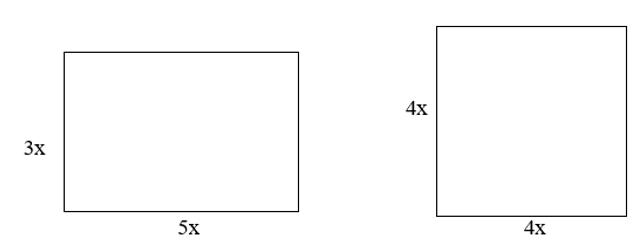
Câu 13. Tính tổng diện tích của hình vuông và hình chữ nhật như hình bên dưới theo biến x.
A. 15x2;
B. 16x2;
C. 31x2;
D. 21x2.
Đáp án: C
Giải thích:
Diện tích hình chữ nhật là: 3x . 5x = 15x2.
Diện tích hình vuông = 4x . 4x = 16x2.
Tính tổng diện tích của hình vuông và hình chữ nhật là: 5x2 + 16x2 = 31x2.
Vậy diện tích của hình vuông và hình chữ nhật trên theo biến x bằng 31x2.
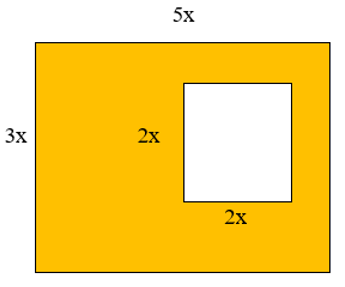
Câu 14. Cho hình vẽ như bên dưới gồm: một hình chữ nhật có chiều dài 5x, chiều rộng 3x và hình vuông nhỏ bên trong có cạnh 2x. Tính diện tích phần tô màu vàng như hình dưới.
A. 15x2;
B. 4x2;
C. 17x2;
D. 11x2.
Đáp án: D
Giải thích:
Diện tích hình chữ nhật là: 5x . 3x = 15x2.
Diện tích hình vuông bên trong là: 2x . 2x = 4x2.
Diện tích phần tô vàng là: 15x2 − 4x2 = 11x2.
Câu 15. Cho hai đa thức A(x) = − 2x + 1 và B(x) = 5x2 + 2x + 9. Tính C(x) tại x = 2 biết C(x) = A(x) + B(x).
A. 30;
B. 40;
C. 23;
D. 10.
Đáp án: A
Giải thích:
Ta có: C(x) = A(x) + B(x)
= − 2x + 1 + (5x2 + 2x + 9)
= − 2x + 1 + 5x2 + 2x + 9
= 5x2 + 10.
Ta có: C(2) = 5 . 22 +10 = 5.4 + 10
= 20 + 10 = 30.
Các câu hỏi trắc nghiệm Toán 7 sách Chân trời sáng tạo có đáp án, chọn lọc khác: