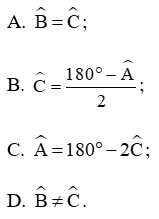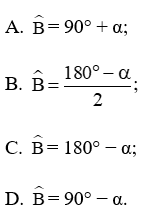Trắc nghiệm Toán 7 Bài 3: Tam giác cân
Bộ 15 bài tập trắc nghiệm Toán 7 Bài 3: Tam giác cân có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 3.
Trắc nghiệm Toán 7 Bài 3: Tam giác cân - Chân trời sáng tạo
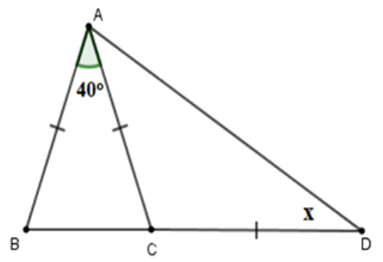
Câu 1. Tính số đo x trên hình vẽ sau:
A. x = 45°;
B. x = 40°;
C. x = 35°;
D. x = 70°.
Đáp án: C
Giải thích:
Ta có tam giác ABC cân tại A (vì AB = AC) có = 40° .
nên = = 70°.
Ta có + = 180° (hai góc kề bù).
suy ra = 180° − = 180° − 70° = 110°.
Ta lại có tam giác CAD cân tại C (vì CA = CD) có = 110°.
Nên x = = = = 35°.
Vậy x = 35°.
Câu 2. Cho tam giác ABC cân tại B. Chọn kết luận đúng nhất.
A. Tam giác ABC có AB = AC;
B. Tam giác ABC đều;
C. Tam giác ABC có ;
D. Tam giác ABC có AC = BC.
Đáp án: C
Giải thích:
Ta có tam giác ABC cân tại B nên AB = BC. Do đó đáp án A và D sai.
Tam giác ABC chưa thể kết luận là tam giác đều vì thiếu điều kiện. Vậy đáp án B sai.
Tam giác ABC cân tại B có (hai góc ở đáy). Vậy đáp án C đúng.
Câu 3. Tam giác cân là tam giác:
A. có hai đường cao bằng nhau;
B. có hai đường trung tuyến bằng nhau;
C. có hai cạnh bên bằng nhau;
D. có hai tia phân giác trong bằng nhau.
Đáp án: C
Giải thích:
Tam giác cân là tam giác có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau.
Vậy đáp án C đúng.
Câu 4. Cho tam giác ABC cân tại A, biết góc B = 50°. Tính số đo các góc còn lại của tam giác đó.
A. = 50°, = 80°;
B. = 80°, = 50°;
C. = 40°, = 90°;
D. = 90°, = 40°.
Đáp án: B
Giải thích:
Ta có tam giác ABC cân tại A suy ra = 50°.
Xét tam giác ABC có:
= 180° (tổng ba góc trong một tam giác).
Suy ra = 180° − ()
= 180° − (50° + 50°)
= 180° – 100° = 80°.
Vậy = 80°; .
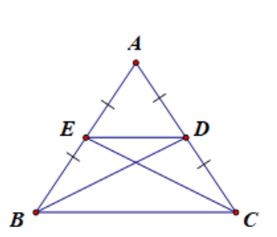
Câu 5. Cho tam giác ABC cân tại A có các đường trung tuyến BD, CE. Tam giác nào dưới đây là tam giác cân?
A. ∆ABD;
B. ∆BCE;
C. ∆ADE;
D. ∆BDE.
Đáp án: C
Giải thích:
Ta có: BD là trung tuyến tam giác ABC suy ra D là trung điểm AC nên AD = DC.
CE là trung tuyến tam giác ABC suy ra E là trung điểm AB nên AE = BE.
Ta có AB = AE + EB và AC = AD + DC.
Mà AB = AC suy ra AE = AD.
Vậy tam giác ADE cân tại A.
Câu 6. Cho tam giác ABC có = 45°. Khi đó tam giác ABC là tam giác gì? Chọn kết luận đúng nhất.
A. Tam giác cân;
B. Tam giác vuông;
C. Tam giác đều;
D. Tam giác vuông cân.
Đáp án: D
Giải thích:
Xét tam giác ABC có:
= 180° (tổng ba góc trong một tam giác).
Suy ra = 180° − ()
= 180° − (45° + 45°) = 180° – 90° = 90°.
Tam giác ABC có = 90°; = 45° nên tam giác ABC là tam giác vuông cân.
Câu 7. Cho tam giác ABC cân tại A. Phát biểu nào sau đây là sai?
Đáp án: D
Giải thích:
Xét tam giác ABC có:
= 180° (tổng 3 góc trong một tam giác)
Suy ra = 180° − () hay = 180° − 2
Mặt khác = 180° suy ra .
Do tam giác ABC cân tại A nên
Vậy đáp án D sai.
Câu 8. Một tam giác cân có góc ở đáy bằng 70° thì số đo góc ở đỉnh là:
A. 54°;
B. 63°;
C. 70°;
D. 40°.
Đáp án: D
Giải thích:
Tổng số đo hai góc ở đáy bằng: 70°.2 = 140°.
Vì tổng ba góc trong tam giác bằng 180° nên số đo góc ở đỉnh tam giác cân này là:
180° − 140° = 40°.
Câu 9. Một tam giác cân có góc ở đáy bằng 52° thì số đo góc ở đỉnh là:
A. 46°;
B. 64°;
C. 67°;
D. 76°.
Đáp án: D
Giải thích:
Tổng số đo hai góc ở đáy bằng: 52°.2 = 104°.
Vì tổng ba góc trong tam giác bằng 180° nên số đo góc ở đỉnh tam giác cân này là:
180° − 104° = 76°.
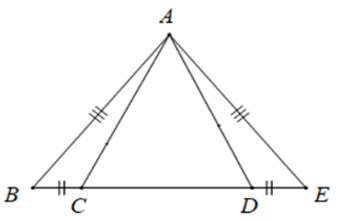
Câu 10. Số tam giác cân trong hình vẽ dưới đây là:
A. 2;
B. 1;
C. 3;
D. 4.
Đáp án: A
Giải thích:
Từ hình vẽ ta có: AB = AE; BC = DE.
Vì AB = AE suy ra ∆ABE cân tại A. Do đó (hai góc ở đáy).
Xét tam giác ABC và tam giác AED có:
(cmt)
AB = AE (gt)
BC = DE (gt)
Suy ra ∆ABC = ∆AED (c.g.c).
Do đó: AC = AD (hai cạnh tương ứng).
Suy ra ∆ACD cân tại A.
Vậy có hai tam giác cân trên hình vẽ.
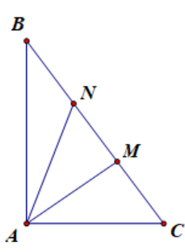
Câu 11. Cho tam giác ABC vuông cân ở A. Trên BC lấy hai điểm M, N sao cho BM = CN = AB. Tính số đo góc MAN.
A. 45°;
B. 30°;
C. 90°;
D. 60°.
Đáp án: A
Giải thích:
Xét tam giác AMN, ta có:
= 180° − = 180° − 135° = 45°.
Vậy = 45°.
Câu 12. Khẳng định nào sau đây là sai?
A. Tam giác đều có ba góc bằng nhau và bằng 60°;
B. Tam giác đều có ba cạnh bằng nhau;
C. Tam giác cân là tam giác đều;
D. Tam giác đều là tam giác cân.
Đáp án: C
Giải thích:
Tam giác đều là tam giác có ba cạnh bằng nhau. Vậy đáp án B đúng
Tam giác đều có mỗi góc bằng nhau và bằng 60°. Vậy đáp án A đúng
Tam giác đều cũng là tam giác cân nhưng tam giác cân chưa chắc là tam giác đều vì nó chỉ có hai cạnh bên bằng nhau.
Vậy đáp án D đúng, C sai.
Câu 13. Cho tam giác ABC có = 90°, AB = AC. Chọn khẳng định đúng nhất.
A. ∆ABC là tam giác vuông;
B. ∆ABC là tam giác vuông cân;
C. ∆ABC là tam giác cân;
D. ∆ABC là tam giác đều.
Đáp án: B
Giải thích:
Xét tam giác ABC có: = 90°; AB = AC.
Vậy tam giác ABC là tam giác vuông cân tại A.
Câu 14. Cho tam giác ABC cân tại A có = 2α. Tính số đo góc B theo α.
Đáp án: D
Giải thích:
Do tam giác ABC cân tại A nên .
Xét tam giác ABC có:
= 180° (tổng ba góc trong một tam giác).
= 180° −
Nên = =
= = 90° − α.
Vậy = 90° − α.
Câu 15. Một tam giác cân có góc ở đáy bằng 40° thì số đo góc ở đỉnh là:
A. 100°;
B. 40°;
C. 140°;
D. 50°.
Đáp án: A
Giải thích:
Giả sử tam giác ABC cân tại A ta có: = 40°.
Xét tam giác ABC có:
= 180° (tổng ba góc trong một tam giác).
Do đó = 180° − − = 180° − 40° − 40° = 100°.
Vậy số đo góc ở đỉnh là 100°.
Các câu hỏi trắc nghiệm Toán 7 sách Chân trời sáng tạo có đáp án, chọn lọc khác: