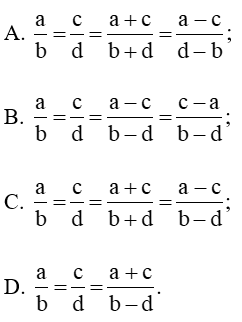Trắc nghiệm Toán 7 Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau
Bộ 15 bài tập trắc nghiệm Toán 7 Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 1.
Trắc nghiệm Toán 7 Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau - Chân trời sáng tạo
Câu 1. Cho x : y : z = 2 : 3 : 5 và x − y + z = − 8. Giá trị của x là:
A. 10;
B. −6;
C. −10;
D. −4.
Đáp án: D
Giải thích:
Ta có x : y : z = 2 : 3 : 5, suy ra
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Suy ra
x = 2 . (−2) = −4;
y = 3 . (−2) = −6;
z = 5 . (−2) = −10.
Vậy chọn đáp án D.
Câu 2. Chọn câu sai. Nếu thì:
A. ad=bc;
B.
C.
D.
Đáp án: C
Giải thích:
Ta có: suy ra
Vậy chọn đáp án C.
Câu 3. Cho tỉ lệ thức . Giá trị của x là:
A. 1;
B. −1;
C. 6;
D. 3.
Đáp án: B
Giải thích:
Ta có
Suy ra
x . 6 = (−2) . 3
x . 6 = −6
x = −1
Vậy x = −1.
Vậy chọn đáp án B.
Câu 4. Cho tỉ lệ thức 5 : x = (−4) : 8. Giá trị của x là:
A. −10;
B. −4;
C. 10;
D. 4.
Đáp án: A
Giải thích:
Ta có 5 : x = (−4) : 8 nên
Suy ra
x . (−4) = 5 . 8
x . (−4) = 40
x = 40 : (−4)
x = −10
Vậy x = −10.
Vậy chọn đáp án A.
Câu 5. Chọn câu sai. Từ đẳng thức −2x = 3y, ta có tỉ lệ thức:
A.
B.
C.
D.
Đáp án: C
Giải thích:
Theo bài ra −2x = 3y. Suy ra (tính chất tỉ lệ thức)
Nếu thì
Do đó là sai.
Vậy chọn đáp án C.
Câu 6. Chọn câu đúng. Chọn dãy tỉ số bằng nhau.
Đáp án: C
Giải thích:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Vậy chọn đáp án C.
Câu 7. Tìm hai số x; y biết và x + y = −24.
A. x = −9; y = −15;
B. x = 9; y = 15;
C. x = −9; y = 15;
D. x = 9; y = 15.
Đáp án: A
Giải thích:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Suy ra x = (−3) . 3 = −9; y = (−3) . 5 = −15.
Vậy chọn đáp án A.
Câu 8. Tìm hai số x và y biết và x − y = −6.
A. x = 8; y = 14;
B. x = −8; y = 14;
C. x = 8; y = −14;
D. x = −8; y = −14.
Đáp án: A
Giải thích:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Suy ra x = 2 . 4 = 8; y = 2 . 7 = 14.
Vậy chọn đáp án A.
Câu 9. Cho 2x = 3y và y − x = −2. Tìm x và y.
A. x = 4; y = 6;
B. x = 6; y = 4;
C. x = −4; y = −6;
D. x = −6; y = −4.
Đáp án: B
Giải thích:
Theo tính chất tỉ lệ thức, ta có 2x = 3y nên
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Suy rax = 2 . 3 = 6; y = 2 . 2 = 4.
Vậy chọn đáp án B.
Câu 10. Cho và 2x + y = 9. Tìm x và y.
A. x = 21; y = 6;
B. x = −6; y = 21;
C. x = 6; y = −21;
D. x = 6; y = 21.
Đáp án: B
Giải thích:
Ta có: suy ra
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra x = (−3).2 = −6; y = (−3).(−7) = 21.
Vậy chọn đáp án B.
Câu 11. Chọn câu sai. Nếu thì:
A.
B.
C.
D.
Đáp án: B
Giải thích:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Vậy chọn đáp án B.
Câu 12. Các tỉ số nào sau đây lập thành một tỉ lệ thức?
A. và
B. và
C.(−3) :7 và 6: (−7);
D. (-1): và
Đáp án: D
Giải thích:
Ta có:
Suy ra
Do đó, và lập thành một tỉ lệ thức.
Vậy chọn đáp án D.
Câu 13. Nếu và 2x + y – z = 6. Giá trị y là:
A. 4;
B. 6;
C. 8;
D. −6.
Đáp án: B
Giải thích:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Suy ra x = 2 . 2 = 4; y = 3 . 2 = 6; z = 4 . 2 = 8.
Vậy x = 4; y = 6; z = 8.
Chọn đáp án B.
Câu 14. Cho hai số dương x, y thoả mãn và xy = 60. Khi đó x, y bằng:
A. x = 6; y = 10;
B. x = 10; y = 6;
C. x = −6; y = −10;
D. x = −10; y = −6.
Đáp án: A
Giải thích:
Đặt . Suy ra x = 3k; y = 5k.
Theo bài ra xy = 60 nên ta có:
3k . 5k = 60
15k2 = 60
k2 = 4
Suy ra k = 2 hoặc k = −2.
Với k = 2 thì x = 3. 2 = 6; y = 5 . 2 = 10
Với k = −2 thì x = 3.(−2) = −6; y = 5 . (−2) = −10
Mà x,y là các số dương nên x = 6; y = 10.
Vậy chọn đáp án A.
Câu 15. Một hình chữ nhật có chu vi 56 m, tỉ số của chiều dài và chiều rộng là 5: 2. Diện tích của hình chữ nhật đó là:
A. 80;
B. 640;
C. 320;
D. 160.
Đáp án: D
Giải thích:
Gọi x, y (m) lần lượt là chiều dài và chiều rộng của hình chữ nhật (0 < x, y < 56).
Nửa chu vi hình chữ nhật là: x + y = 56 : 2 = 28 (m)
Tỉ số của chiều dài và chiều rộng là 5 : 2 nên hay
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra x = 5 . 4 = 20; y = 2 . 4 = 8 (thoả mãn điều kiện)
Khi đó, hình chữ nhật có chiều dài là 20 m và chiều rộng là 8 m.
Vậy diện tích hình chữ nhật là: 20 . 8 = 160 (m2).
Vậy chọn đáp án D.
Các câu hỏi trắc nghiệm Toán 7 sách Chân trời sáng tạo có đáp án, chọn lọc khác: