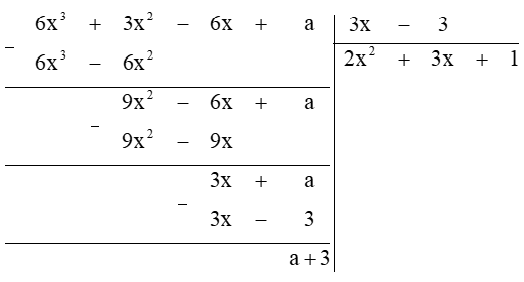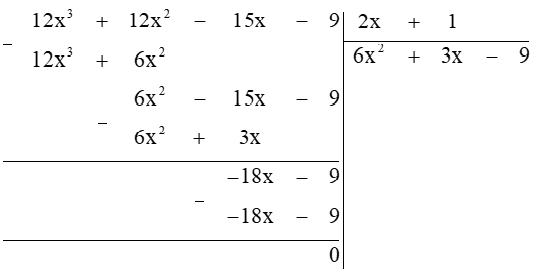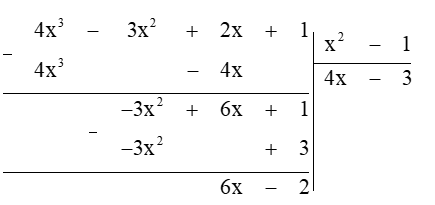Bài tập cuối chương 7
Bộ 30 Bài tập cuối chương 7 có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài tập cuối chương 7.
Trắc nghiệm Toán 7 Bài tập cuối chương 7 - Chân trời sáng tạo
Câu 1. Cho biểu thức sau: (5 − x) + [(−14 − 5x2) + (9 + x)]. Rút gọn biểu thức đã cho ta được biểu thức nào trong các biểu thức sau đây?
A. 5x2;
B. −5x2;
C. x2 − 5;
D. x2.
Đáp án: B
Giải thích:
Ta có: (5 − x) + [(−14 − 5x2) + (9 + x)]
= 5 − x − 14 − 5x2 + 9 + x
= − 5x2 + (x – x) + (5 − 14 + 9)
= −5x2.
Câu 2. Tính giá trị của biểu thức A = x2 (y − 2) + 7xy + 10y2 khi x = 2; y = 1
A. 16;
B. 18;
C. 20;
D. 10.
Đáp án: C
Giải thích:
Thay x = 2; y = 3 vào biểu thức A, ta được:
A = 22 . (1 − 2) + 7 . 2 . 1 + 10 . 12
= 4 . (−1) + 14 + 10
= −4 + 14 + 10 = 20.
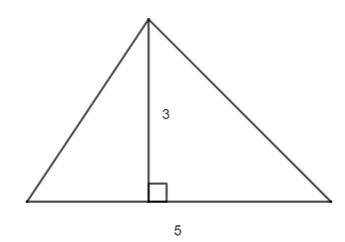
Câu 3. Biểu thức số của diện tích hình tam giác có chiều cao bằng 3 và cạnh đáy bằng 5 là:
A. 3 . 5;
B. ;
C. 2 . 2 . 5;
D. 2 . 5.
Đáp án: B
Giải thích:
Diện tích hình tam giác bằng tích của chiều cao nhân độ dài đáy chia cho 2 nên ta có biểu thức số biểu thị diện tích tam giác.
Câu 4. Trong túi có 3 màu bi gồm: màu xanh, màu đỏ và màu vàng. Số viên bi xanh là 5x2 + 3, số viên bi đỏ là 2x2 + 3x và số viên bi vàng là 5. Biểu thức đại số biểu thị tổng số viên bi trong túi là biểu thức nào trong các biểu thức sau đây?
A. 5x2 + 3x + 8;
B. 7x2 + 3x + 3;
C. 7x2 + 3x + 8;
D. 7x2 + 8x + 5.
Đáp án: C
Giải thích:
Tổng số viên bi trong túi là:
(5x2 + 3) + (2x2 + 3x) + 5
= 5x2 + 3 + 2x2 + 3x + 5
= (5x2 + 2x2) + 3x + (5 + 3)
= 7x2 + 3x + 8.
Biểu thức đại số biểu thị tổng số viên bi trong túi là: 7x2 + 3x + 8.
Câu 5. Trong các biểu thức sau đây, biểu thức nào là đơn thức một biến?
A. x2 + 2x + 1;
B. 4y + 12;
C.9x;
D. y3 + 13y − 5.
Đáp án: C
Giải thích:
Đơn thức một biến là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và biến đó .
Do đó 9x là đơn thức một biến.
Câu 6. Trong các biểu thức sau đây, có bao nhiêu đa thức một biến:
2 ; ; 3x2 − 2 ; .
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: B
Giải thích:
Theo định nghĩa, đa thức một biến là tổng của những đơn thức cùng một biến và đơn thức một biến cũng là đa thức một biến.
Do đó chỉ có 2 và 3x2 − 2 là đa thức một biến.
Vậy trong 4 đa thức trên có 2 đa thức một biến.
Câu 7. Tìm bậc của đa thức sau: y − 3 +5y2 − 6y5 + y4.
A. 1;
B. 2;
C. 4;
D. 5.
Đáp án: D
Giải thích:
Trong đa thức trên, số mũ cao nhất của y là 5.
Do đó bậc của đa thức đã cho là 5.
Câu 8. Tập các nghiệm của đa thức B(x) = 3x2 − 12 trong tập hợp {0; 2; −2; 3} là:
A.{0; 2};
B. {0; 3};
C. {2; −2};
D. {2}.
Đáp án: C
Giải thích:
Theo định nghĩa: Nếu đa thức B(x) có giá trị bằng 0 tại x = a thì ta nói a là một nghiệm của đa thức đó.
Thay từng phần tử trong tập hợp trên vào đa thức B(x) ta được:
B(0) = 3 . 02 − 12 = −12;
B(2) = 3 . 22 − 12 = 3 . 4 − 12 = 12 − 12 = 0;
B(−2) = 3 . (−2)2 − 12 = 3 . 4 − 12 = 12 − 12 = 0;
B(3) = 3 . 32 − 12 = 3 . 9 − 12 = 27 − 12 = 15.
Vậy {2; −2} là nghiệm của đa thức B(x).
Câu 9. Cho hai đa thức:M(x) = x3 − 2x + 1 và N(x) = x2 + 2x − 5. Tính M(x) + N(x).
A. x3 − 4x − 4;
B. x3 + x2 − 6;
C. x3 + x2 − 4x − 4;
D. x3 + x2 − 4.
Đáp án: D
Giải thích:
M(x) + N(x) = (x3 − 2x + 1) + (x2 + 2x − 5)
= x3 − 2x + 1 + x2 + 2x − 5
= x3 + x2 + (−2x + 2x) + (1 − 5)
= x3 + x2 – 4.
Câu 10. Cho đa thức A(x) = x4 + 3x3 + 2x; B(x) = x3 + 2; C(x) = −x4 + 2x3 − 9 .
Tính A(x) − B(x) + C(x).
A. 4x3 + 2x − 11;
B. 4x3 − 2x − 11;
C. 2x4 + 4x3 + 2x − 11;
D. 4x3 + 2x + 11.
Đáp án: A
Giải thích:
Ta có: A(x) − B(x) + C(x)
= (x4 + 3x3 + 2x) − (x3 + 2) + (−x4 + 2x3 − 9)
= x4 + 3x3 + 2x − x3 − 2 − x4 + 2x3 − 9
= (x4 − x4) + (3x3 − x3 + 2x3) + 2x + (− 2 − 9)
= 4x3 + 2x – 11.
Câu 11. Trong kì thi học sinh giỏi, học sinh tại các trường thuộc Thành phố Hồ Chí Minh được các huy chương sau: vàng, bạc, đồng. Trong đó số huy chương vàng bằng 2x4 − x2 + 3, số huy chương bạc bằng x3 − 1. Biểu thức biểu thị số huy chương đồng của các học sinh tại các trường thuộc Thành phố Hồ Chí Minh, biết tổng tất cả các huy chương bằng 3x4 + x3 − 5.
A. x4 + x2 − 7;
B. x4 + x2 + 7;
C. x4 + 2x2 − 7;
D. x4 + x3 − x2 − 7.
Đáp án: A
Giải thích:
Biểu thức biểu thị tổng số huy chương vàng và bạc của các học sinh tại các trường thuộc Thành phố Hồ Chí Minh là:
(2x4 − x2 + 3) + (x3 − 1)
= 2x4 − x2 + 3 + x3 − 1
= 2x4 + x3 − x2 + (3 − 1)
= 2x4 + x3 − x2 + 2.
Biểu thức biểu thị số huy chương đồng của các học sinh tại các trường thuộc Thành phố Hồ Chí Minh là:
3x4 + x3 − 5 − (2x4 + x3 − x2 + 2)
= 3x4 + x3 − 5 − 2x4 − x3 + x2 − 2
= (3x4 − 2x4) + (x3 − x3) + x2 + (−5 − 2)
= x4 + x2 – 7.
Vậy biểu thức biểu thị số huy chương đồng của học sinh tại các trường thuộc Thành phố Hồ Chí Minh là x4 + x2 – 7.
Câu 12. Cho biểu thức: 2x2 − x(2x + 3) + 3 . (x + 2). Sau khi rút gọn thì biểu thức trở thành:
A. 6;
B. 2x2 − 3x;
C. 0;
D. 3x.
Đáp án: A
Giải thích:
Ta có: 2x2 − x(2x + 3) + 3 . (x + 2)
= 2x2 − 2x2 − 3x + 3x + 6
= (2x2 − 2x2) +(− 3x + 3x) + 6= 6.
Câu 13. Tích của hai đa thức −3x + 2 và 7x − 5 là:
A. 21x2 + 29x − 10;
B. −21x2 + 29x − 10;
C. 21x2 + 29x + 10;
D. −21x2 + 19x − 10.
Đáp án: B
Giải thích:
Ta có: (−3x + 2)(7x − 5)
= (−3x) . (7x − 5) + 2 . (7x − 5)
= −21x2 + 15x + 14x − 10
= −21x2 + (15x + 14x) − 10
= −21x2 + 29x – 10.
Câu 14. Tìm a để đa thức 6x3 + 3x2 − 6x + a chia hết cho 3x – 3.
A. 3;
B. 6;
C. 4;
D. −3.
Đáp án: D
Giải thích:
Thực hiện phép tính, ta được:
Vậy để đa thức 6x3 + 3x2 − 6x + a chia hết cho 3x − 3 thì a + 3 = 0.
Do đó a = −3 để đa thức 6x3 + 3x2 − 6x + a chia hết cho 3x – 3.
Câu 15. Kết quả của phép tính: 36 . (−x3 + 4x2 − 5x) . tại x = 2 là:
A. −6;
B. 0;
C. 6;
D. 5.
Đáp án: A
Giải thích:
Ta có : 36 . (−x3 + 4x2 − 5x) .
= 36 . [(-x3 + 4x2 - 5x).]
= 36 . [.(-x3 + 4x2 - 5x)]
= (36.). (−x3 + 4x2 − 5x)
= 3 . (−x3 + 4x2 − 5x)
= −3x3 + 12x2 − 15x (1)
Thay x = 2 vào (1) ta được:
(−3) . 23 + 12 . 22 − 15 . 2
= (−3) . 8 + 12 . 4 − 15 . 2
= (−24) + 48 − 30 = −6.
Vậy kết quả của phép tính: 36 . (−x3 + 4x2 − 5x) . tại x = 2 bằng −6.
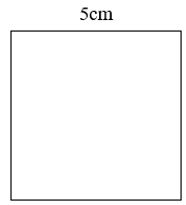
Câu 16. Biểu thức số biểu thị chu vi hình vuông có cạnh bằng 5 cm là:
A. 2 . 5;
B. 4 . 5;
C. 3 . 5;
D. 5 . 5.
Đáp án: B
Giải thích:
Hình vuông có cạnh bằng 5 cm nên biểu thức số của chu vi của hình vuông bằng 4 . 5.
Câu 17. Rút gọn biểu thức: 5(x2 − x) + 2x2 + 7x, ta được biểu thức nào trong các biểu thức sau đây?
A. 7x2 + 2x;
B. 5x2− 5x + 2x2 + 7x;
C. 5x2− 5x;
D. 2x2 − 7x.
Đáp án: A
Giải thích:
Ta có: 5(x2 − x) + 2x2 + 7x
= 5x2 − 5x + 2x2 + 7x
= (5 + 2).x2 + ( −5 + 7).x
= 7x2 + 2x.
Câu 18. Giá trị của biểu thức (a − b)2 − 2c khi a = 9, b = 4, c = 5 bằng bao nhiêu?
A. 5;
B. 10;
C. 25;
D. 15.
Đáp án: D
Giải thích:
Thay a = 9, b = 4, c = 5 vào biểu thức trên, ta được:
(9 − 4)2 − 2.5 = 52 − 10
= 25 − 10 = 15.
Câu 19. Rút gọn biểu thức: 2x(x − y) + 3y(y − x) − 2y2 − 2x2 ta được biểu thức nào trong các biểu thức sau?
A. y2 − 5xy;
B. x − 2xy + y2;
C. −5xy;
D.2x2 + 3y2.
Đáp án: A
Giải thích:
Ta có: 2x(x − y) + 3y(y − x) − 2y2 − 2x2
= 2x2 − 2xy + 3y2 − 3xy − 2y2 − 2x2
= (2 − 2).x2 + (3 − 2).y2 + (−2 − 3).xy
= y2 − 5xy.
Câu 20. Cho biết giá bán của một chiếc lò vi sóng tại một cửa hàng là T− aT (triệu đồng), với T là giá gốc và a là mã giảm giá áp dụng cho khách hàng thân thiết. Tính giá bán của chiếc lò vi sóng khi được giảm giá với T= 3 (triệu đồng) và a= 10%.
A. 2 triệu đồng;
B. 2,7 triệu đồng;
C. 1 triệuđồng;
D. 1,5 triệu đồng.
Đáp án: B
Giải thích:
Thay T = 3 và a = 10% vào biểu thứcT – aT, ta được:
T – aT = 3 − 10%. 3 = 3 − 0,3 = 2,7 (triệu đồng)
Vậy giá bán của chiếc lò vi sóng khi được giảm giá là 2,7 triệu đồng.
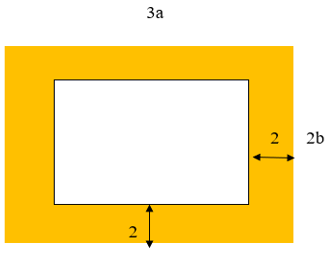
Câu 21. Một thửa ruộng hình chữ nhật (như hình vẽ) có chiều dài bằng 3a, chiều rộng bằng 5b. Người ta xây thêm phần đê xung quanh mảnh ruộng rộng 2 m. Tính diện tích phần đê xung quanh mảnh ruộng, biết a = 5 m, b = 2 m.
A. 150 m2;
B. 66m2;
C. 40 m2;
D. 84 m2.
Đáp án: D
Giải thích:
Diện tích thửa ruộng ban đầu là:
3a . 2b = 3 . 5 . 5 . 2 = 150 (m2)
Diện tích còn lại của mảnh ruộng là:
(3a − 2 − 2) . (5b − 2 − 2)
= (3 . 5 − 2 − 2) . (5 . 2 − 2 − 2)
= 11 . 6 = 66 (m2)
Diện tích phần đê xung quanh là:
150 − 66 = 84 (m2).
Vậy diện tích phần đê xung quanh mảnh ruộng bằng 84 m2.
Câu 22. Cho hai đa thức A(x) = − 2x + 1 và B(x) = 5x2 + 2x + 9. Tính C(x) tại x = 2 biết C(x) = A(x) + B(x).
A. 30;
B. 40;
C. 23;
D. 10.
Đáp án: A
Giải thích:
Ta có: C(x) = A(x) + B(x)
= − 2x + 1 + (5x2 + 2x + 9)
= − 2x + 1 + 5x2 + 2x + 9
= 5x2 + 10.
Ta có: C(2) = 5 . 22 +10 = 5.4 + 10
= 20 + 10 = 30.
Câu 23. Cho đa thức: P(y) = y2 − 10 + 3y2 − 9y + 4 − 7y.
Rút gọn biểu thức sau và sắp xếp theo lũy thừa tăng của biến y, ta được đa thức nào trong các đa thức sau đây?
A. y2 − 10 − 9y;
B. 6 − 2y + 4y2;
C. − 6 − 16y + 4y2;
D. − 6 + 16y + 4y2.
Đáp án: C
Giải thích:
Ta có: P(y) = y2 − 10 + 3y2 − 9y + 4 − 7y
= −10 + 4 − 9y − 7y + y2 + 3y2
= (−10 + 4) + (−9 − 7)y + (1 + 3)y2
= −6 − 16y + 4y2.
Vậy rút gọn và sắp xếp theo lũy thừa giảm của biến y thì biểu thức: P(y) = −6 − 16y + 4y2.
Câu 24. Diện tích một hình vuông được tính bởi biểu thức S(x) = x2. Tính giá trị của S biết x là nghiệm của đa thức P(x) = 2x – 8.
A. 16;
B. 25;
C. 36;
D. 9.
Đáp án: A
Giải thích:
Theo đề bài, x là nghiệm của đa thức P(x) = 2x – 8 nên ta có:
P(x) = 2x − 8 = 0
Suy ra x = 4
Ta có: S(4) = 42 = 16.
Vậy diện tích hình vuông bằng 16.
Câu 25. Cho đa thức U(x) = 7x2 + 4x − 3. Tìm đa thức V(x) sao cho U(x) + V(x) = x3 + x2 –5.
A. V(x) = x3 − 6x2 − 4x − 2;
B. V(x) = 6x2 − 4x − 2;
C. V(x) = x3 − 8x2 + 5x +13;
D. V(x) = x3 − 6x2 − 2.
Đáp án: A
Giải thích:
Ta có: U(x) = 7x2 + 4x − 3
Vì U(x) + V(x) = x3 + x2 −5 nên
V(x) = x3 + x2 − 5 − U(x)
= x3 + x2 − 5 − (7x2 + 4x − 3)
= x3 + x2 − 5 − 7x2 − 4x + 3
= x3 + (x2 − 7x2) − 4x + (−5 + 3)
= x3 − 6x2 − 4x – 2.
Vậy V(x) = x3 − 6x2 − 4x – 2.
Câu 26. Cho ba đa thức A(x) = x2 − 3x +10; B(x) = 3x3 +16; C(x) = 2x4 − 4x2 − 8x.
Tính A(x) − B(x) − C(x).
A. −2x4 − 3x3 + 5x2 + 5x − 6;
B. 2x4 + 3x3 − 3x2 − 11x +26;
C. −2x4 − 3x3 − 3x2 + 5x − 6;
D. −2x4 − 3x3 + 5x2 − 11x − 6.
Đáp án: A
Giải thích:
Ta có: A(x) − B(x) = (x2 − 3x +10) − (3x3 +16)
= x2 − 3x + 10 − 3x3 − 16
= − 3x3 + x2 − 3x + (10 − 16)
= − 3x3 + x2 − 3x – 6.
Khi đó: A(x) − B(x) − C(x)
= (−3x3 + x2 − 3x − 6) − (2x4 − 4x2 − 8x)
= −3x3 + x2 − 3x − 6 − 2x4 + 4x2 + 8x
= −2x4 − 3x3 + (x2 + 4x2) + (−3x + 8x) − 6
= −2x4 − 3x3 + 5x2 + 5x – 6.
Vậy A(x) − B(x) − C(x) = −2x4 − 3x3 + 5x2 + 5x – 6.
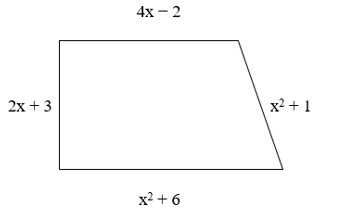
Câu 27. Biểu thức biểu thị chu vi của hình thang vuông như hình bên dưới là:
A. x2 + 6x + 4;
B. 2x2 − 6x + 8;
C. 2x2 + 2x + 8;
D. 2x2 + 6x + 8.
Đáp án: D
Giải thích:
Chu vi của hình thang bằng tổng độ dài hai cạnh đáy và hai cạnh bên. Khi đó:
P = (4x −2 + x2 + 6) + (2x + 3 + x2 + 1) (với P là chu vi của hình thang)
= 4x − 2 + x2 + 6 + 2x + 3 + x2 + 1
= (x2 + x2) + (4x + 2x)+ (−2 + 6 + 3 + 1)
= 2x2 + 6x +8.
Vậy chu vi của hình thang vuông trên được biểu thị bằng biểu thức 2x2 + 6x +8.
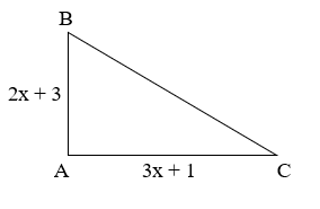
Câu 28. Cho tam giác vuông (như hình bên dưới) có chu vi bằng 14x – 4. Tính cạnh BC của tam giác ABC.
A. 9x − 8;
B. 9x + 8;
C. 7x − 8;
D. 9x + 4.
Đáp án: A
Giải thích:
Chu vi tam giác trên bằng tổng độ dài ba cạnh nên ta có:
P = AB + AC + BC (với P là chu vi của hình tam giác)
Suy ra BC = P − AB − AC
= 14x − 4 − (2x +3) − (3x+1)
= 14x − 4 − 2x − 3 − 3x − 1
= (14x − 2x − 3x) + (−4 − 3 − 1)
= 9x – 8.
Vậy BC = 9x – 8.
Câu 29. Phép chia đa thức (12x3 + 12x2 − 15x − 9) cho đa thức (2x + 1) được đa thức thương là:
A. 6x2 + 3x − 9;
B. 6x2 + 6x − 9;
C. 6x2 + 3x + 9;
D. 6x2 + 5x − 9.
Đáp án: A
Giải thích:
Thực hiện phép tính chia, ta được:
Vậy đa thức thương của phép chia đa thức trên bằng 6x2 + 3x – 9.
Câu 30. Thương và phần dư của phép chia đa thức (4x3 − 3x2 + 2x + 1) cho đa thức (x2 − 1) lần lượt là:
A. 4x + 3; 6x − 2;
B. 2x + 3; 3x − 1;
C.4x − 3; 0;
D. 4x − 3; 6x − 2.
Đáp án: D
Giải thích:
Thực hiện phép tính, ta được:
Vậy phép chia đa thức trên có thương bằng 4x − 3 và phần dư bằng 6x – 2.
Các câu hỏi trắc nghiệm Toán 7 sách Chân trời sáng tạo có đáp án, chọn lọc khác: