Trắc nghiệm Toán 10 Bài 2: Hoán vị, chỉnh hợp và tổ hợp

Bộ 15 bài tập trắc nghiệm Toán 10 Bài 2: Hoán vị, chỉnh hợp và tổ hợp có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 2.

335

Tải tài liệu

« Trang trước

Trang sau »

Trắc nghiệm Toán 10 Bài 2: Hoán vị, chỉnh hợp và tổ hợp - Chân trời sáng tạo

I. Nhận biết

Câu 1. Cho tập hợp A có n phần tử (n ≥ 1) và số nguyên k (1 ≤ k ≤ n). Phát biểu nào sau đây sai?

A. Một chỉnh hợp chập k của n phần tử trên là mỗi cách lấy k phần tử của tập A và sắp xếp chúng theo một thứ tự;

B. Một hoán vị của tập A là mỗi cách sắp xếp n phần tử của tập A theo một thứ tự;

C. Một tổ hợp chập k của n phần tử là mỗi cách lấy k phần tử của A;

D. Mỗi hoán vị của n phần tử cũng chính là tổ hợp chập n của n phần tử đó.

Hiển thị đáp án

Đáp án: D

Giải thích:

⦁ Mỗi cách sắp xếp n phần tử của tập A theo một thứ tự gọi là một hoán vị các phần tử đó. Do đó phương án B là phát biểu đúng.

⦁ Mỗi cách lấy k phần tử của A và sắp xếp chúng theo một thứ tự gọi là một chỉnh hợp chập k của n phần tử đó. Do đó phương án A là phát biểu đúng.

⦁ Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử. Do đó phương án C là phát biểu đúng.

⦁ Mỗi hoán vị của n phần tử cũng chính là chỉnh hợp chập n của n phần tử đó. Do đó phương án D là phát biểu sai.

Vậy ta chọn phương án D.

Câu 2. Cho n ≥ 1, n ∈ ℤ và 1 ≤ k ≤ n. Phát biểu nào sau đây sai?

A. P₀ = 1;

B. $P_{n} = C_{n}^{n}$ ;

C. $C_{n}^{k} = C_{n}^{n - k}$ ;

D. $A_{n}^{k} = k! . C_{n}^{k}$

Hiển thị đáp án

Đáp án: B

Giải thích:

⦁ Ta quy ước: P₀ = 0! = 1. Do đó phương án A đúng.

⦁ Ta có $C_{n}^{k} = C_{n}^{n - k}$ , với 0 ≤ k ≤ n.

⦁ Ta có $P_{n} = A_{n}^{n}$ . Do đó phương án B sai.

Do đó phương án C đúng.

⦁ Ta có $k! . C_{n}^{k} = k! . \frac{n!}{k! . (n - k)!} = \frac{n!}{(n - k)!} = A_{n}^{k}$ .

Do đó phương án D đúng.

Vậy ta chọn phương án B.

Câu 3. Giá trị của $A_{12}^{4}$ bằng:

A. 12.11.10.9.8.7.6.5.4;

B. 4.3.2.1;

C. 12.11.10.9;

D. 8!.

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $A_{12}^{4} = 12. (12 - 1) . (12 - 2) . (12 - 3) = 12.11.10.9$ .

Do đó ta chọn phương án C.

Câu 4. Cho tập hợp M = {a; b; c}. Số hoán vị của ba phần tử của M là:

A. 4;

B. 5;

C. 6;

D. 7.

Hiển thị đáp án

Đáp án: C

Giải thích:

Số hoán vị của ba phần tử của tập M là: P₃ = 3! = 3.2.1 = 6.

Vậy ta chọn phương án C.

Câu 5. Giá trị của $C_{n}^{0} - C_{n}^{1} + C_{n}^{n - 1} - C_{n}^{n}$ bằng:

A. 0

B. 1;

C. n;

D. 2n.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $C_{n}^{0} - C_{n}^{1} + C_{n}^{n - 1} - C_{n}^{n} = C_{n}^{0} - C_{n}^{1} + C_{n}^{1} - C_{n}^{0} = 0.$

Vậy ta chọn phương án A.

Câu 6. Giá trị của $C_{10}^{7}$ bằng:

A. 120;

B. 604 800;

C. 35;

D. 720.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $C_{10}^{7} = \frac{10!}{7! . (10 - 7)!} = \frac{10.9.8.7!}{7! .3!} = \frac{10.9.8}{3.2.1} = \frac{720}{6} = 120$

Vậy ta chọn phương án A.

Câu 7. Cho tập hợp X gồm n phần tử (n ≥ 1) và số nguyên k (1 ≤ k ≤ n). Một chỉnh hợp chập k của n phần tử là:

A. Một kết quả bất kì của sự sắp xếp k phần tử bất kì của tập hợp X;

B. Một kết quả của việc lấy k phần tử từ n phần tử của tập X và sắp xếp chúng theo một thứ tự nào đó;

C. Một số được tính bởi công thức: n(n – 1)(n – 2)…(n – k + 1);

D. Một kết quả của việc lấy k phần tử từ n phần tử của tập X.

Hiển thị đáp án

Đáp án: B

Giải thích:

Mỗi cách lấy k phần tử của tập X và sắp xếp chúng theo một thứ tự gọi là một chỉnh hợp chập k của n phần tử đó.

Vậy ta chọn phương án B.

II. Thông hiểu

Câu 1. Một tổ học sinh có 5 nam và 5 nữ xếp thành một hàng dọc thì số các cách xếp khác nhau là:

A. 25;

B. 10!;

C. 10;

D. 40.

Hiển thị đáp án

Đáp án: B

Giải thích:

Tổ học sinh có tổng cộng 5 + 5 = 10 học sinh.

Mỗi cách xếp khác nhau là một hoán vị của 10 phần tử.

Do đó số cách xếp 10 học sinh thành một hàng dọc là: 10! cách xếp.

Vậy ta chọn phương án B.

Câu 2. Một lớp có 30 học sinh. Hỏi có bao nhiêu cách chọn 3 học sinh để làm vệ sinh lớp học trong một ngày?

A. 4 060;

B. 900;

C. 24 360;

D. 90.

Hiển thị đáp án

Đáp án: A

Giải thích:

Mỗi cách chọn 3 học sinh để làm vệ sinh lớp học trong một ngày là một tổ hợp chập 3 của 30 phần tử.

Do đó số cách phân công 3 học sinh là: $C_{30}^{3} = 4060$ .

Vậy ta chọn phương án A.

Câu 3. Từ danh sách gồm 9 học sinh của lớp 10A, bầu ra một ủy ban gồm một chủ tịch, một phó chủ tịch, một thư kí và một ủy viên. Hỏi có bao nhiêu khả năng cho kết quả bầu ủy ban này?

A. 84;

B. 126;

C. 3 024;

D. 6 561.

Hiển thị đáp án

Đáp án: C

Giải thích:

Mỗi cách chọn 4 học sinh trong 9 học sinh để bầu ra một ban gồm một chủ tịch, một phó chủ tịch, một thư kí và một ủy viên là một chỉnh hợp chập 4 của 9 phần tử.

Do đó số khả năng có thể về kết quả bầu uỷ ban này là: $A_{9}^{4} = 3 024$ .

Vậy ta chọn phương án C.

Câu 4. Có ba môn thi Toán, Vật lí, Hóa học cần xếp vào 3 buổi thi, mỗi buổi một môn sao cho môn Toán không thi buổi đầu thì số cách xếp là:

A. 6;

B. 2;

C. 4;

D. 5.

Hiển thị đáp án

Đáp án: C

Giải thích:

Việc xếp mỗi buổi một môn sao cho môn Toán không thi buổi đầu có hai phương án thực hiện:

Phương án 1: Môn Vật lí thi buổi đầu, thì số cách xếp hai môn còn lại vào 2 buổi còn lại là 2! cách xếp.

Phương án 2: Môn Hóa học thi buổi đầu, thì số cách xếp hai môn còn lại vào 2 buổi còn lại là 2! cách xếp.

Theo quy tắc cộng, ta có tất cả 2! + 2! = 2 + 2 = 4 cách xếp.

Vậy ta chọn phương án C.

Câu 5. Có bao nhiêu cách chọn và sắp xếp thứ tự 5 cầu thủ để đá luân lưu, biết rằng cả 11 cầu thủ đều có khả năng như nhau?

A. 55 440;

B. 20 680;

C. 32 456;

D. 41 380.

Hiển thị đáp án

Đáp án: A

Giải thích:

Mỗi cách chọn và sắp xếp thứ tự 5 cầu thủ trong số 11 cầu thủ là một chỉnh hợp chập 5 của 11 phần tử.

Do đó số cách chọn và sắp xếp thứ tự 5 cầu thủ là: $A_{11}^{5} = 55 440$ cách chọn.

Vậy ta chọn phương án A.

Câu 6. Trong một bình đựng 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên 2 viên bi. Có bao nhiêu cách lấy được 2 viên bi cùng màu?

A. 18;

B. 9;

C. 22;

D. 4.

Hiển thị đáp án

Đáp án: B

Giải thích:

Việc lấy được 2 viên bi cùng màu có 2 phương án thực hiện:

Phương án 1: Lấy được 2 viên bi màu đỏ, có $C_{4}^{2}$ cách chọn.

Phương án 2: Lấy được 2 viên bi màu xanh, có $C_{3}^{2}$ cách chọn.

Do đó theo quy tắc cộng, ta có tất cả $C_{4}^{2} + C_{3}^{2} = 9$ cách chọn.

Vậy ta chọn phương án B.

Câu 7. Có bao nhiêu số lẻ có 4 chữ số khác nhau được lập thành từ các chữ số 1; 2; 5; 6; 9?

A. 15;

B. 120;

C. 72;

D. 12.

Hiển thị đáp án

Đáp án: C

Giải thích:

Việc lập số theo yêu cầu có 2 công đoạn thực hiện:

Công đoạn 1: Chọn chữ số ở hàng đơn vị là chữ số lẻ, có 3 cách chọn (từ các chữ số 1; 5; 9).

Công đoạn 2: Chọn 3 chữ số còn lại, có $A_{4}^{3}$ cách chọn.

Do đó theo quy tắc nhân, ta có tất cả $3. A_{4}^{3} = 72$ số.

Vậy ta chọn phương án C

Câu 8. Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là:

A. 60;

B. 180;

C. 330;

D. 90.

Hiển thị đáp án

Đáp án: A

Giải thích:

Trắc nghiệm Toán 10 Bài 2: Hoán vị, chỉnh hợp và tổ hợp (ảnh 1)

III. Vận dụng

Câu 1. Một hội đồng gồm 5 nam và 4 nữ được bầu vào một ban quản trị gồm 4 người. Biết rằng ban quản trị có ít nhất một nam và một nữ. Số cách bầu chọn là:

A. 240;

B. 260;

C. 126;

D. 120.

Hiển thị đáp án

Đáp án: A

Giải thích:

Trắc nghiệm Toán 10 Bài 2: Hoán vị, chỉnh hợp và tổ hợp (ảnh 1)

Câu 2. Từ các chữ số 0; 1; 2; 3; 4; 5, có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau và chia hết cho 9?

A. 16;

B. 18;

C. 20;

D. 14.

Hiển thị đáp án

Đáp án: A

Giải thích:

Gọi $\bar{a b c}$ là số cần tìm, với a, b, c ∈ {0; 1; 2; 3; 4; 5}.

Vì $\bar{a b c} ⋮ 9$ nên tổng các chữ số a + b + c ⋮ 9.

Khi đó a; b; c là bộ số (0; 4; 5), (2; 3; 4) hoặc (1; 3; 5).

Trường hợp 1: a; b; c là bộ số (0; 4; 5).

Vị trí a có 2 cách chọn (số 4 hoặc số 5).

Vị trí b, c có 2! = 2 cách chọn từ 2 chữ số còn lại.

Do đó theo quy tắc nhân, ta có tất cả 2.2 = 4 số.

Trường hợp 2: a; b; c là bộ số (2; 3; 4) thì có 3! = 6 số.

Trường hợp 3: a; b; c là bộ số (1; 3; 5) thì có 3! = 6 số.

Vậy theo quy tắc cộng, ta có tất cả 4 + 6 + 6 = 16 số.

Ta chọn phương án A.

Câu 3. Có bao nhiêu số tự nhiên n thỏa mãn $14. P_{3} . C_{n - 1}^{n - 3} < A_{n + 1}^{4}$ ?

A. 1;

B. 2;

C. 3;

D. Vô số.

Hiển thị đáp án

Đáp án: D

Giải thích:

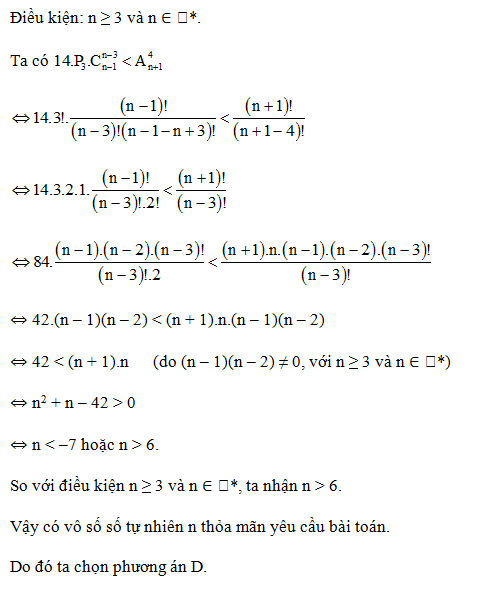
Trắc nghiệm Toán 10 Bài 2: Hoán vị, chỉnh hợp và tổ hợp (ảnh 1)

Câu 4. Đẳng thức nào sau đây sai?

A. $C_{2023}^{23} = C_{2022}^{23} + C_{2022}^{22}$ ;

B. $C_{2023}^{23} = C_{2022}^{2000} + C_{2022}^{22}$ ;

C. $C_{2023}^{23} = C_{2022}^{2000} + C_{2022}^{1999}$ ;

D. $C_{2023}^{23} = C_{2022}^{23} + C_{2022}^{2000}$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Trắc nghiệm Toán 10 Bài 2: Hoán vị, chỉnh hợp và tổ hợp (ảnh 1)

Câu 5. Trong 10 câu hỏi, trong đó có 4 câu lý thuyết và 6 câu bài tập, người ta cần soạn các đề thi. Biết rằng trong đề thi phải gồm 3 câu hỏi trong đó có cả hai dạng câu hỏi đó. Hỏi có thể soạn được bao nhiêu đề có yêu cầu như trên?

A. 69;

B. 88;

C. 96;

D. 100.

Hiển thị đáp án

Đáp án: C

Giải thích:

Việc soạn được 1 đề thi thỏa mãn yêu cầu bài toán có 2 phương án thực hiện:

Phương án 1: Chọn 1 câu hỏi lý thuyết và 2 câu hỏi bài tập.

Chọn 1 câu hỏi lý thuyết trong số 4 câu lý thuyết thì có $C_{4}^{1}$ cách chọn.

Chọn 2 câu hỏi bài tập trong số 6 câu hỏi bài tập thì có $C_{6}^{2}$ cách chọn.

Do đó theo quy tắc nhân, ta có tất cả $C_{4}^{1} . C_{6}^{2}$ đề được soạn.