Trắc nghiệm Toán 10 Bài 2: Giải phương trình bậc hai một ẩn
Bộ 15 bài tập trắc nghiệm Toán 10 Bài 2: Giải phương trình bậc hai một ẩn có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 2.
Trắc nghiệm Toán 10 Bài 2: Giải phương trình bậc hai một ẩn - Chân trời sáng tạo
I. Nhận biết
Câu 1. Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn?
A. 3x2 – 12x + 1 ≤ 0;
B. 2x3 + 5 > 0;
C. x2 + x – 1 = 0;
D. –x + 7 > 0.
Đáp án: A
Giải thích:
Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng:
ax2 + bx + c ≤ 0; ax2 + bx + c < 0; ax2 + bx + c ≥ 0; ax2 + bx + c > 0 với a ≠ 0.
Trong bốn phương án A, B, C, D, ta thấy chỉ có phương án A là có dạng bất phương trình bậc hai một ẩn dạng ax2 + bx + c ≤ 0 với a = 3, b = – 12 và c = 1.
Ta chọn phương án A.
Câu 2. Giá trị x nào sau đây là nghiệm của bất phương trình bậc hai một ẩn –x2 + 2x + 1 ≥ 0?
A. x = 5;
B. x = 2;
C. x = 7;
D. x = –1.
Đáp án: B
Giải thích:
Bất phương trình –x2 + 2x + 1 ≥ 0.
⦁ Xét phương án A:
Vì –52 + 2.5 + 1 = –14 < 0.
Nên x = 5 không là nghiệm của bất phương trình –x2 + 2x + 1 ≥ 0.
Do đó phương án A sai.
⦁ Xét phương án B:
Vì –22 + 2.2 + 1 = 1 > 0.
Nên x = 2 là nghiệm của bất phương trình –x2 + 2x + 1 ≥ 0.
Do đó phương án B đúng.
⦁ Xét phương án C:
Vì –72 + 2.7 + 1 = –34 < 0.
Nên x = 7 không là nghiệm của bất phương trình –x2 + 2x + 1 ≥ 0.
Do đó ta loại phương án C.
⦁ Xét phương án D:
Vì –(–1)2 + 2.(–1) + 1 = –2 < 0.
Nên x = –1 không là nghiệm của bất phương trình –x2 + 2x + 1 ≥ 0.
Do đó ta loại phương án D.
Vậy ta chọn phương án B.
Câu 3. Giá trị của m để (m – 1)x2 – 2(m + 1)x + m + 3 ≤ 0 là bất phương trình bậc hai một ẩn là:
A. m ≠ –3;
B. m ≠ –1;
C. m = 1;
D. m ≠ 1.
Đáp án: D
Giải thích:
Để bất phương trình đã cho là bất phương trình bậc hai một ẩn thì a ≠ 0.
Nghĩa là, m – 1 ≠ 0 do đó m ≠ 1.
Vậy ta chọn phương án D.
Câu 4. Cho x2 + 2x – 1 ≤ 2x2 – 5x + 5. Ta đưa được bất phương trình trên về dạng:
A. Bất phương trình bậc hai ẩn x dạng ax2 + bx + c ≤ 0 với a = –1, b = 7, c = –6;
B. Bất phương trình bậc nhất ẩn x dạng ax + b ≤ 0 với a = –1, b = 6;
C. Bất phương trình bậc hai ẩn x dạng ax2 + bx + c ≥ 0 với a = –1, b = 7, c = –6;
D. Bất phương trình bậc hai ẩn x dạng ax2 + bx + c ≤ 0 với a = 1, b = –7, c = 6.
Đáp án: A
Giải thích:
Ta có x2 + 2x – 1 ≤ 2x2 – 5x + 5.
⇔ (x2 – 2x2) + (2x + 5x) – 1 – 5 ≤ 0.
⇔ –x2 + 7x – 6 ≤ 0
⇔ x2 – 7x + 6 ≥ 0
Do đó ta có thể đưa được bất phương trình x2 + 2x – 1 ≤ 2x2 – 5x + 5 về dạng:
• ax2 + bx + c ≤ 0, với a = –1, b = 7, c = –6.
• ax2 + bx + c ≥ 0, với a = 1, b = –7, c = 6.
Vậy ta chọn phương án A.
Câu 5. Cho –2x2 – mx + 1 ≤ (m – 3)x2 – 8. Khẳng định nào sau đây đúng?
A. Với m = 0 thì ta được bất phương trình bậc hai ẩn x dạng ax2 + bx + c ≤ 0 (với a > 0).
B. Với m = 1 thì ta được bất phương trình bậc hai ẩn x dạng ax2 + bx + c ≤ 0 (với a ≠ 0).
C. Với m = –2 thì ta được bất phương trình bậc hai ẩn x dạng ax2 + bx + c ≤ 0 (với a < 0).
D. Với m = 3 thì ta được bất phương trình bậc hai ẩn x dạng ax2 + bx + c ≤ 0 (với a > 0).
Đáp án: A
Giải thích:
Ta có –2x2 – mx + 1 ≤ (m – 3)x2 – 8.
⇔ [–2 – (m – 3)]x2 – mx + 1 + 8 ≤ 0.
⇔ (1 – m)x2 – mx + 9 ≤ 0.
• Với m = 0, ta có bất phương trình (1 – 0)x2 – 0.x + 9 ≤ 0.
⇔ x2 + 9 ≤ 0.
Đây là bất phương trình bậc hai ẩn x dạng ax2 + bx + c ≤ 0 với a = 1 > 0.
Do đó phương án A đúng.
• Với m = 1, ta có bất phương trình (1 – 1)x2 – 1.x + 9 ≤ 0.
⇔ –x + 9 ≤ 0. Đây không phải bất phương trình bậc hai ẩn x.
Do đó phương án B sai.
• Với m = –2, ta có bất phương trình [1 – (–2)]x2 – (–2)x + 9 ≤ 0.
⇔ 3x2 + 2x + 9 ≤ 0.
Đây là bất phương trình bậc hai ẩn x dạng ax2 + bx + c ≤ 0 với a = 3 > 0.
Do đó phương án C sai.
• Với m = 3, ta có bất phương trình (1 – 3)x2 – 3x + 9 ≤ 0.
⇔ –2x2 – 3x + 9 ≤ 0.
Đây là bất phương trình bậc hai ẩn x dạng ax2 + bx + c ≤ 0 với a = –2 < 0.
Do đó phương án D sai.
Vậy ta chọn phương án A.
Câu 6. Cho bất phương trình f(x) = ax2 + bx + c ≤ 0, biết a > 0 và f(x) có hai nghiệm phân biệt x1; x2 sao cho x1 < x2. Khi đó tập nghiệm của bất phương trình là:
A. (–∞; x1);
B. (x2; +∞);
C. [x1; x2];
D. (x1; x2).
Đáp án: C
Giải thích:
Theo đề, ta có f(x) = ax2 + bx + c (với a > 0) có hai nghiệm phân biệt x1; x2 sao cho x1 < x2.
Suy ra:
⦁ f(x) dương với mọi x thuộc hai khoảng (–∞; x1) và (x2; +∞);
⦁ f(x) âm với mọi x thuộc khoảng (x1; x2);
⦁ f(x) = 0 khi x = x1 hoặc x = x2.
Vậy bất phương trình ax2 + bx + c ≤ 0 có tập nghiệm là [x1; x2].
Ta chọn phương án C.
Câu 7. Cho bất phương trình f(x) = ax2 + bx + c > 0, biết a < 0 và f(x) có nghiệm kép x0. Khi đó tập nghiệm của bất phương trình là:
A. (–∞; x0) ∪ (x0; +∞);
B. ∅;
C. {x0};
D. ℝ.
Đáp án: B
Giải thích:
Theo đề, ta có f(x) = ax2 + bx + c > 0 (với a < 0) và có nghiệm kép x0.
Suy ra:
⦁ f(x) âm với mọi x thuộc hai khoảng (–∞; x0) và (x0; +∞);
⦁ f(x) = 0 khi x = x0.
Vậy bất phương trình ax2 + bx + c > 0 vô nghiệm.
Khi đó tập nghiệm của bất phương trình ax2 + bx + c > 0 là: ∅.
Ta chọn phương án B.
II. Thông hiểu
Câu 1. Cho f(x) = –x2 – 4x + 5. Có bao nhiêu giá trị nguyên của x thỏa mãn f(x) ≥ 0?
A. 5;
B. 7;
C. 10;
D. Vô số.
Đáp án: B
Giải thích:
Tam thức bậc hai f(x) = –x2 – 4x + 5 có ∆’ = (–2)2 – (–1).5 = 9 > 0.
Suy ra f(x) có hai nghiệm phân biệt là:
Ta lại có a = –1 < 0.
Do đó ta có:
⦁ f(x) âm trên hai khoảng (–∞; –5) và (1; +∞);
⦁ f(x) dương trên khoảng (–5; 1);
⦁ f(x) = 0 khi x = –5 hoặc x = 1.
Vì vậy bất phương trình f(x) ≥ 0 có tập nghiệm là [–5; 1].
Trên đoạn [–5; 1], ta thấy có 7 giá trị nguyên là: –5; –4; –3; –2; –1; 0; 1.
Vậy ta chọn phương án B.
Câu 2. Tập nghiệm của bất phương trình x2 – 3x + 2 < 0 là:
A. (1; 2);
B. (–∞; 1) ∪ (2; +∞);
C. (–∞; 1);
D. (2; +∞).
Đáp án: A
Giải thích:
Tam thức bậc hai f(x) = x2 – 3x + 2 có ∆ = (–3)2 – 4.1.2 = 1 > 0.
Do đó f(x) có hai nghiệm phân biệt là:
Ta lại có a = 1 > 0.
Do đó ta có:
⦁ f(x) âm trên khoảng (1; 2);
⦁ f(x) dương trên hai khoảng (–∞; 1) và (2; +∞);
⦁ f(x) = 0 khi x = 1 hoặc x = 2.
Vì vậy bất phương trình x2 – 3x + 2 < 0 có tập nghiệm là (1; 2).
Ta chọn phương án A.
Câu 3. Tập nghiệm của bất phương trình x2 + 9 > 6x là:
A. (3; +∞);
B. ℝ \ {3};
C. ℝ;
D. (–∞; 3).
Đáp án: B
Giải thích:
Ta có x2 + 9 > 6x.
⇔ x2 – 6x + 9 > 0.
Tam thức bậc hai f(x) = x2 – 6x + 9 có ∆’ = (–3)2 – 1.9 = 0.
Suy ra f(x) có nghiệm kép x = 3.
Ta lại có a = 1 > 0.
Do đó ta có:
⦁ f(x) dương trên hai khoảng (–∞; 3) và (3; +∞);
⦁ f(x) = 0 khi x = 3.
Vì vậy bất phương trình x2 – 6x + 9 > 0 có tập nghiệm là (–∞; 3) ∪ (3; +∞) (hoặc ta có thể viết: ℝ \ {3}).
Ta chọn phương án B.
Câu 4. Tập xác định của hàm số là:
A. (1; 3);
B. (–∞; –1) ∪ (3; +∞);
C. [–1; –3];
D. (–∞; –1] ∪ [3; +∞).
Đáp án: C
Giải thích:
Hàm số xác định khi và chỉ khi –x2 + 2x + 3 ≥ 0.
Tam thức bậc hai f(x) = –x2 + 2x + 3 có ∆’ = 12 – (–1).3 = 4 > 0.
Do đó f(x) có hai nghiệm phân biệt là:
Ta lại có a = –1 < 0.
Do đó ta có:
⦁ f(x) dương trên khoảng (–1; 3);
⦁ f(x) âm trên hai khoảng (–∞; –1) và (3; +∞);
⦁ f(x) = 0 khi x = –1 hoặc x = 3.
Vì vậy bất phương trình –x2 + 2x + 3 ≥ 0 có tập nghiệm là [–1; 3].
Khi đó hàm số đã cho có tập xác định là [–1; 3].
Ta chọn phương án C.
Câu 5. Tập xác định của hàm số là:
A. ℝ;
B. (2; 6);
C. ∅;
D. (–∞; 2) ∪ (6; +∞).
Đáp án: C
Giải thích:
Hàm số xác định khi và chỉ khi –2x2 + 8x – 12 > 0.
Tam thức bậc hai f(x) = –2x2 + 8x – 12 có ∆’ = 42 – (–2).(–12) = –8 < 0.
Do đó f(x) vô nghiệm.
Ta lại có a = –2 < 0.
Vì vậy f(x) < 0, với mọi x ∈ ℝ.
Vậy bất phương trình –2x2 + 8x – 12 > 0 có tập nghiệm là ∅.
Ta chọn phương án C.
Câu 6. Cho bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0. Để x = 6 là một nghiệm của bất phương trình trên thì m nhận giá trị nào trong các giá trị sau đây?
A. ;
B. ;
C. ;
D. .
Đáp án: A
Giải thích:
Vì x = 6 là một nghiệm của bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0 nên ta có:
(m – 2).62 + 2(2m – 3).6 + 5m – 6 ≥ 0.
⇔ 36(m – 2) + 12(2m – 3) + 5m – 6 ≥ 0
⇔ 65m – 114 ≥ 0
Vậy thỏa mãn yêu cầu bài toán.
Ta chọn phương án A.
Câu 7. Cho hàm số bậc hai f(x) có đồ thị như hình bên.
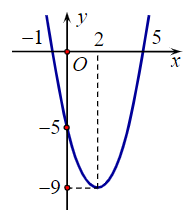
Tập nghiệm của bất phương trình f(x) ≥ 0 là:
A. (–1; 5);
B. (–∞; –1) ∪ (5; +∞);
C. (–∞; –1] ∪ [5; +∞);
D. [–1; 5].
Đáp án: C
Giải thích:
Quan sát đồ thị, ta thấy f(x) ≥ 0 khi và chỉ khi x ≤ –1 hoặc x ≥ 5.
Vì vậy tập nghiệm của bất phương trình f(x) ≥ 0 là (–∞; –1] ∪ [5; +∞).
Ta chọn phương án C.
Câu 8. Tập nghiệm của bất phương trình (2x – 5)(x + 2) ≥ x2 – 4 là:
A. [–2; 3);
B. (–∞; –2) ∪ (3; +∞).;
C. ℝ;
D. (–∞; –2] ∪ [3; +∞).
Đáp án: D
Giải thích:
Ta có (2x – 5)(x + 2) ≥ x2 – 4.
⇔ 2x2 – x – 10 ≥ x2 – 4.
⇔ x2 – x – 6 ≥ 0.
Tam thức bậc hai f(x) = x2 – x – 6 có ∆ = (–1)2 – 4.1.(–6) = 25 > 0.
Suy ra f(x) có hai nghiệm phân biệt là:
Ta lại có a = 1 > 0.
Vì vậy:
⦁ f(x) dương với mọi x thuộc hai khoảng (–∞; –2) và (3; +∞);
⦁ f(x) âm với mọi x thuộc khoảng (–2; 3);
⦁ f(x) = 0 khi x = –2 hoặc x = 3.
Vậy bất phương trình x2 – x – 6 ≥ 0 có tập nghiệm là (–∞; –2] ∪ [3; +∞).
Do đó ta chọn phương án D.
III. Vận dụng
Câu 1. Với giá trị nào của tham số m thì x = 2m + 3 là một nghiệm của bất phương trình x2 + 2(m – 1)x + m2 – 3m + 4 ≤ 0?
A. m ≥ 0;
B. m < 0;
C. m ∈ ℝ;
D. m ∈ ∅.
Đáp án: D
Giải thích:
Vì x = 2m + 3 là một nghiệm của bất phương trình x2 + 2(m – 1)x + m2 – 3m + 4 ≤ 0 nên ta có:
(2m + 3)2 + 2(m – 1)(2m + 3) + m2 – 3m + 4 ≤ 0.
⇔ 4m2 + 12m + 9 + 2(2m2 + m – 3) + m2 – 3m + 4 ≤ 0.
⇔ 9m2 + 11m + 7 ≤ 0.
Tam thức bậc hai f(m) = 9m2 + 11m + 7 có ∆ = 112 – 4.9.7 = – 131 < 0.
Do đó f(m) vô nghiệm.
Ta lại có am = 9 > 0.
Vì vậy f(m) > 0, với mọi m ∈ ℝ.
Do đó bất phương trình f(m) = 9m2 + 11m + 7 ≤ 0 vô nghiệm.
Vậy không có m thỏa mãn yêu cầu bài toán.
Ta chọn phương án D.
Câu 2. Tập hợp các giá trị của m để hàm số có tập xác định là ℝ là:
A. ;
B. ;
C. m ∈ ∅;
D. .
Đáp án: C
Giải thích:
Hàm số đã cho có tập xác định là ℝ khi và chỉ khi (2 – 3m)x2 + 2mx + m – 1 > 0 với mọi x ∈ ℝ.
Đặt f(x) = (2 – 3m)x2 + 2mx + m – 1.
Trường hợp 1: a = 0 ⇔ 2 – 3m = 0 ⇔ m =
Với , ta có
.
Do đó không thỏa mãn.
Trường hợp 2: a ≠ 0.
Khi đó f(x) là tam thức bậc hai có:
∆’ = m2 – (2 – 3m)(m – 1)
= m2 – (–3m2 + 5m – 2)
= 4m2 – 5m + 2.
Để f(x) > 0 với mọi x ∈ ℝ thì a > 0 và ∆ < 0.
(1)
Ta giải bất phương trình 4m2 – 5m + 2 < 0 như sau:
Tam thức bậc hai g(m) = 4m2 – 5m + 2 có ∆ = (–5)2 – 4.4.2 = –7 < 0.
Do đó g(m) vô nghiệm.
Ta lại có am = 4 > 0.
Vì vậy g(m) > 0, với mọi giá trị của m ∈ ℝ.
Do đó không có giá trị nào của m thỏa mãn g(m) = 4m2 – 5m + 2 < 0.
Vì vậy không có giá trị nào của m để (1) thỏa mãn.
Kết hợp cả hai trường hợp, ta thu được m ∈ ∅.
Vậy ta chọn phương án C.
Câu 3. Giá trị nào của m để phương trình (m2 – m – 6)x2 – 2(m + 2)x – 4 = 0 có nghiệm?
A. m ∈ (–∞; –2) \ {3};
B. m ∈ (–∞; –2] ∪ [2; +∞);
C. m ∈ [2; +∞) \ {3};
D. m ∈ (–∞; –2) ∪ [2; +∞) \ {3}.
Đáp án: D
Giải thích:
Phương trình f(x) = (m2 – m – 6)x2 – 2(m + 2)x – 4 = 0.
+) Trường hợp 1: a = 0 ⇔ m2 – m – 6 = 0
⇔ m = 3 hoặc m = –2.
• Với m = 3, ta có 0.x2 – 2.(3 + 2)x – 4 = 0
⇔ –10x – 4 = 0 ⇔ x = .
Do đó m = 3 thỏa mãn.
• Với m = –2, ta có 0.x2 – 2(–2 + 2)x – 4 = 0.
⇔ 0.x – 4 = 0 (vô nghiệm)
Do đó m = –2 không thỏa mãn.
+) Trường hợp 2: a ≠ 0 ⇔ m ≠ 3 và m ≠ –2.
f(x) là tam thức bậc hai ẩn x có:
∆’ = (m + 2)2 – (m2 – m – 6).(–4)
= m2 + 4m + 4 + 4m2 – 4m – 24
= 5m2 – 20
Phương trình f(x) = 0 có nghiệm khi và chỉ khi ∆’ ≥ 0
⇔ 5m2 – 20 ≥ 0
Tam thức bậc hai f(m) = 5m2 – 20 có ∆ = 02 – 4.5.(–20) = 400 > 0.
Do đó f(m) có hai nghiệm phân biệt là: m1 = –2, m2 = 2.
Ta lại có a = 5 > 0.
Vì vậy:
⦁ f(m) dương với mọi m thuộc hai khoảng (–∞; –2) và (2; +∞);
⦁ f(m) âm với mọi m thuộc khoảng (–2; 2);
⦁ f(m) = 0 khi m = –2 hoặc m = 2.
Do đó bất phương trình 5m2 – 20 ≥ 0 có tập nghiệm là (–∞; –2] ∪ [2; +∞).
So với điều kiện m ≠ 3 và m ≠ –2, ta nhận m ∈ (–∞; –2) ∪ [2; +∞) \ {3}.
Kết hợp cả hai trường hợp, ta thu được m ∈ (–∞; –2) ∪ [2; +∞) \ {3}.
Vậy ta chọn phương án D.
Câu 4. Lợi nhuận I thu được từ việc giảm giá một loại xe gắn máy của một doanh nghiệp tư nhân là một tam thức bậc hai I(x) = 200x2 – 1400x + 2400, trong đó x là số tiền giảm giá (triệu đồng) và 0 ≤ x ≤ 5. Với số tiền giảm giá là bao nhiêu thì doanh nghiệp đó không có lãi?
A. Dưới 3 triệu đồng;
B. Từ 3 đến 4 triệu đồng;
C. Trên 4 triệu đồng;
D. Giảm giá 5 triệu đồng.
Đáp án: B
Giải thích:
Tam thức bậc hai I(x) = 200x2 – 1400x + 2400 có:
∆’ = (–700)2 – 200.2400 = 10 000 > 0.
Suy ra I(x) có hai nghiệm phân biệt là:
Ta lại có a = 200 > 0 và 0 ≤ x ≤ 5.
Vì vậy ta có bảng xét dấu sau:
|
x |
0 |
|
3 |
|
4 |
|
5 |
|
f(x) |
|
+ |
0 |
– |
0 |
+ |
|
Theo bảng xét dấu ta có:
⦁ I(x) dương với mọi x thuộc hai khoảng [0; 3) và (4; 5];
⦁ I(x) âm với mọi x thuộc khoảng (3; 4);
⦁ I(x) = 0 khi x = 3 hoặc x = 4.
Do đó doanh nghiệp đó không có lãi khi và chỉ khi I(x) ≤ 0.
Tức là khi x ∈ [3; 4].
Hay ta có thể nói là khi cửa hàng giảm giá từ 3 đến 4 triệu đồng thì doanh nghiệp đó không có lãi.
Vậy ta chọn phương án B.
Câu 5. Một mảnh đất hình chữ nhật có chu vi là 150 m. Để diện tích của mảnh đất đó lớn hơn 650 m2 thì chiều dài của mảnh đất phải:
A. Lớn hơn 10 m;
B. Lớn hơn 37,5 m;
C. Từ 10 m đến 65 m;
D. Từ 37,5 m đến 65 m.
Đáp án: D
Giải thích:
Gọi x (m) là chiều dài của mảnh đất hình chữ nhật (x > 0).
Mảnh đất hình chữ nhật có chu vi là 150 m nên có nửa chu vi là 75 m.
Khi đó chiều rộng của mảnh đất là: 75 – x (m).
Do chiều dài luôn lớn hơn chiều rộng nên x > 75 – x hay x > 37,5.
Diện tích của mảnh đất là: x(75 – x) = –x2 + 75x (m2).
Theo đề ta có diện tích của mảnh đất đó lớn hơn 650 m2.
⇔ –x2 + 75x > 650.
+) Xét tam thức bậc hai f(x) = –x2 + 75x – 650 có:
∆ = 752 – 4.(–1).(–650) = 3025 > 0.
Suy ra f(x) có hai nghiệm phân biệt là:
Ta lại có a = –1 < 0 và x > 37,5 nên:
⦁ f(x) âm với mọi x thuộc hai khoảng (0; 37,5) và (65; +∞);
⦁ f(x) dương với mọi x thuộc khoảng (37,5; 65);
⦁ f(x) = 0 khi x = 37,5 hoặc x = 65.
Do đó bất phương trình –x2 + 75x – 650 ≥ 0 có tập nghiệm là [37,5; 65].
Khi đó chiều dài của mảnh đất phải từ 37,5 m đến 65 m thì diện tích của mảnh đất đó lớn hơn 650 m2.
Vậy ta chọn phương án D.
Các câu hỏi trắc nghiệm Toán 10 sách Chân trời sáng tạo có đáp án, chọn lọc khác:


