Quảng cáo
3 câu trả lời 4408
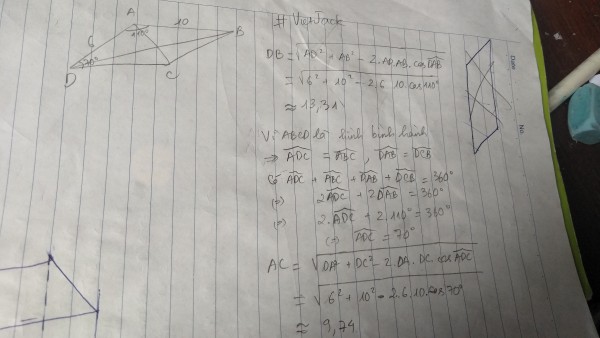
Gọi $\vec{a} = \vec{AB}$ và $\vec{b} = \vec{AD}$.
Ta có $\vec{AC} = \vec{AB} + \vec{BC} = \vec{AB} + \vec{AD} = \vec{a} + \vec{b}$.
$\vec{BD} = \vec{BA} + \vec{AD} = -\vec{a} + \vec{b}$.
Độ dài của $\vec{a}$ là $|\vec{a}| = AB = 10.6$.
Độ dài của $\vec{b}$ là $|\vec{b}| = AD = AB = 10.6$. (Vì ABCD là hình bình hành)
Góc giữa $\vec{a}$ và $\vec{b}$ là $\angle(\vec{a}, \vec{b}) = \angle DAB = 110^\circ$.
Theo định lý cosin, ta có:
$|\vec{AC}|^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2|\vec{a}||\vec{b}|\cos(110^\circ)$
$AC^2 = 10.6^2 + 10.6^2 - 2(10.6)(10.6)\cos(110^\circ)$
$AC^2 = 2(10.6)^2 (1 - \cos(110^\circ))$
$AC^2 = 2(112.36)(1 - (-0.342)) = 2(112.36)(1.342) = 301.46$
$AC = \sqrt{301.46} \approx 17.36$
$|\vec{BD}|^2 = |-\vec{a} + \vec{b}|^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2|\vec{a}||\vec{b}|\cos(180^\circ - 110^\circ)$
$BD^2 = 10.6^2 + 10.6^2 - 2(10.6)(10.6)\cos(70^\circ)$
$BD^2 = 2(10.6)^2 (1 - \cos(70^\circ))$
$BD^2 = 2(112.36)(1 - 0.342) = 2(112.36)(0.658) = 147.97$
$BD = \sqrt{147.97} \approx 12.16$
Vậy $AC \approx 17.4$ và $BD \approx 12.2$
Quảng cáo
Câu hỏi hot cùng chủ đề
-
6 122242
-
4 80506
-
45771
