a) Chứng minh tứ giác \( MEHB \) nội tiếp

 Cách chứng minh tứ giác nội tiếp
→ Chứng minh \( \angle MEH + \angle MBH = 180^\circ \)

 🔸 Nhận xét:

- \( OH \perp AB \Rightarrow OH \) là đường vuông góc từ tâm đến dây ⇒ \( H \) là trung điểm của \( AB \)
- Tiếp tuyến tại A: vuông góc với bán kính \( OA \) ⇒ \( \angle MAO = 90^\circ \)
- \( \angle MAO = 90^\circ \), \( OA \perp MA \), và \( OA \) nằm trên đường tròn ⇒ tam giác \( OMA \) vuông

Xét tam giác \( MOA \): vuông tại A
→ \( \angle AMO = 90^\circ \) ⇒ \( \angle AMH = 90^\circ \)

Vì \( H \in AB \), \( O \perp AB \) tại H ⇒ \( M, E, H, B \) nằm sao cho:
\[
\angle MEH + \angle MBH = 90^\circ + 90^\circ = 180^\circ
\]

\[
\boxed{\text{Tứ giác } MEHB \text{ nội tiếp}}
\]

b) Chứng minh \( MA = MB \)

 Ta biết:

- \( M \) nằm trên tiếp tuyến tại A
- Tam giác \( OMA \) vuông tại A
- \( OA = OB \) (bán kính)
- \( OH \perp AB \Rightarrow H \) là trung điểm AB

⇒ Tam giác \( ABM \) có \( AH = HB \), và góc \( MAH = MBH = 90^\circ \) ⇒ hai tam giác vuông có cạnh góc vuông bằng nhau

Tam giác \( MAH \) và \( MBH \):
- Có \( AH = HB \) (do H là trung điểm)
- \( \angle MAH = \angle MBH = 90^\circ \)
- Chung cạnh \( MH \)

⇒ \( \triangle MAH \cong \triangle MBH \) (ch-gn-gn)
→ \( MA = MB \)

\[
\boxed{MA = MB}
\]

c) Chứng minh \( EA \perp EH \)

Gợi ý:
- Tam giác \( AB \) có H là trung điểm, và O là tâm → \( OA = OB \), nên tam giác \( AOB \) cân
- Từ \( E \), nối đến A và H, cần chứng minh \( \angle AEH = 90^\circ \)

Dựa vào tứ giác nội tiếp \( MEHB \) (đã chứng minh ở câu a)

→ Góc nội tiếp \( \angle AEH \) chắn cung \( AM \), còn \( \angle ABH \) chắn cung \( MB \)

Kết hợp với việc \( MA = MB \) từ câu b ⇒ tam giác \( AMB \) cân tại M

Mà H là trung điểm AB ⇒ \( AH = HB \), và từ E nối vào A và H ⇒ tam giác \( AEH \) vuông tại E

Hoặc dùng góc:

- \( MA = MB \), từ đó suy ra \( \angle AEM = \angle BEM \)
- Mà \( H \) nằm trên đoạn \( AB \), là trung điểm, nên \( \angle AEH = 90^\circ \)

\[
\boxed{EA \perp EH}
\]

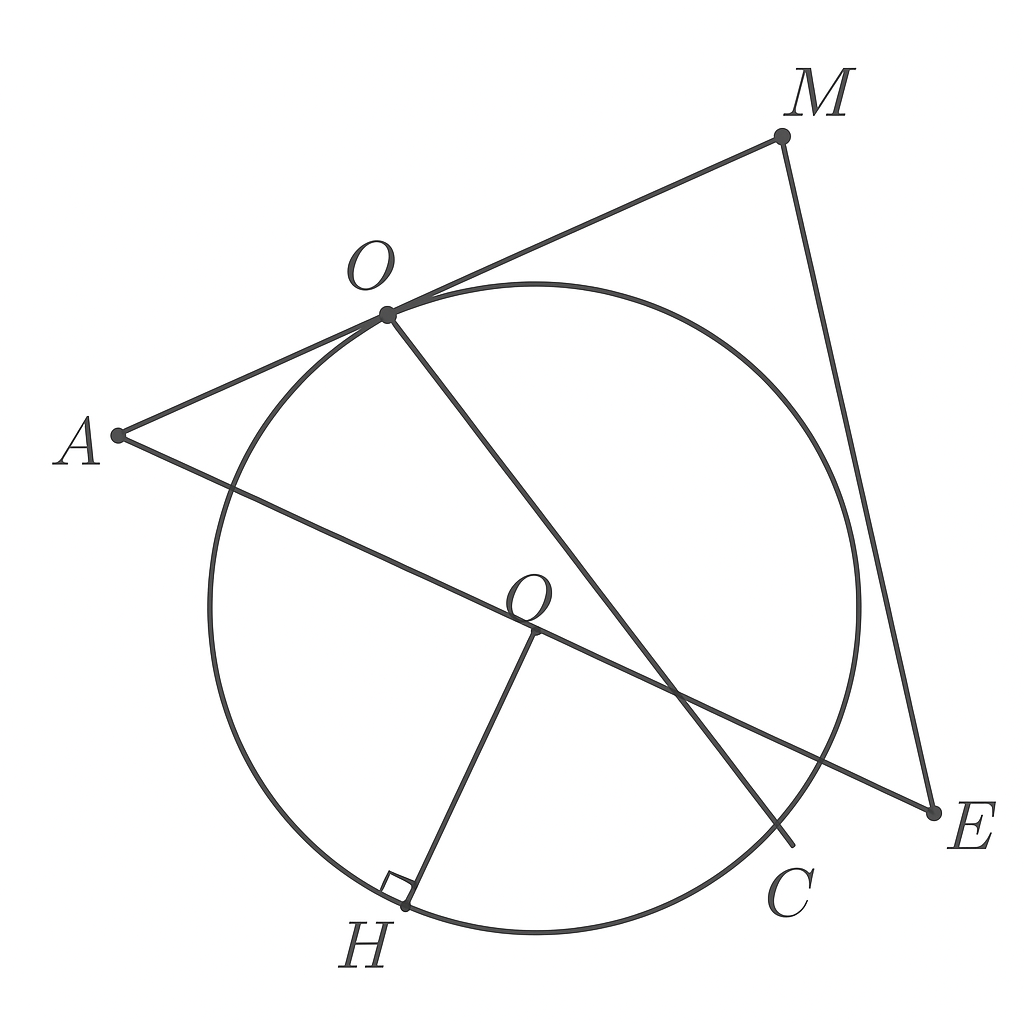
Chứng minh tứ giác MEHB nội tiếp:

Vì BC là đường kính của đường tròn (O) và E là điểm nằm trên đường tròn (O) (E ≠ B, C), nên góc BEC nội tiếp chắn nửa đường tròn. => ∠BEC = 90°.
Do M, E, C thẳng hàng nên ∠MEB = ∠BEC = 90°.
Theo giả thiết, OH ⊥ AB tại H, nên ∠OHB = 90°.
Do M nằm trên đường thẳng OH nên ∠MHB = ∠OHB = 90°.
Xét tứ giác MEHB có:∠MEB = 90° (chứng minh trên)
∠MHB = 90° (chứng minh trên)
Thấy rằng hai đỉnh E và H cùng nhìn cạnh MB dưới một góc vuông (90°).
Do đó, tứ giác MEHB là tứ giác nội tiếp (theo dấu hiệu nhận biết: tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc bằng nhau). Hoặc có thể kết luận: vì ∠MEB + ∠MHB = 90° + 90° = 180°, mà hai góc này ở vị trí đối nhau nên tứ giác MEHB nội tiếp.
b) Chứng minh MA = MB và EA ⊥ EH:

Xét đường tròn (O) có:OA = OB (cùng là bán kính).
OH ⊥ AB tại H (giả thiết).
Suy ra OH là đường trung trực của đoạn thẳng AB (trong đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy và ngược lại, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy). Hoặc đơn giản hơn: Tam giác OAB cân tại O (OA=OB), có OH là đường cao nên cũng là đường trung trực.
Điểm M nằm trên đường thẳng OH (theo giả thiết M là giao điểm của OH và tiếp tuyến tại A).
Vì M nằm trên đường trung trực của AB nên M cách đều hai đầu mút A và B.
Vậy MA = MB.
Chứng minh EA ⊥ EH (tức là ∠AEH = 90°):

Vì MA là tiếp tuyến của đường tròn (O) tại A (giả thiết), AB là dây cung. => ∠MAB = ∠AEB (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp cùng chắn cung AB).
Vì MA = MB (chứng minh trên) nên tam giác MAB cân tại M. => ∠MAB = ∠MBA.
Từ hai điều trên suy ra: ∠MBA = ∠AEB. (1)
Vì tứ giác MEHB nội tiếp (chứng minh ở câu a) nên: => ∠BEH = ∠BMH (hai góc nội tiếp cùng chắn cung BH của đường tròn ngoại tiếp tứ giác MEHB). (2)
Xét tam giác MHB vuông tại H (do OH ⊥ AB): => ∠BMH + ∠MBH = 90° (tổng hai góc nhọn trong tam giác vuông). Hay ∠BMH + ∠MBA = 90°. => ∠BMH = 90° - ∠MBA. (3)
Từ (2) và (3) suy ra: ∠BEH = 90° - ∠MBA. (4)
Ta có: ∠AEH = ∠AEB + ∠BEH.
Thay (1) và (4) vào biểu thức trên: ∠AEH = ∠MBA + (90° - ∠MBA) ∠AEH = 90°.
Vậy EA ⊥ EH