Quảng cáo
2 câu trả lời 108
a) Chứng minh tứ giác MEHB nội tiếp
Ta chứng minh tổng hai góc đối của tứ giác MEHB bằng 180∘, ví dụ:
∠MEB+∠MHB=180∘
⇒ Tam giác MOA vuông tại A
⇒ ∠MAO=90∘
Mà OH⊥AB tại H ⇒ ∠MHB=90∘
Mặt khác, từ hình học đường tròn:
- ∠MEB=∠MCB (do cùng chắn cung MB)
- ∠MCB=90∘ (vì BC là đường kính, tam giác nội tiếp chắn nửa đường tròn)
⇒ ∠MEB=90∘, ∠MHB=90∘
→ Tổng: ∠MEB+∠MHB=180∘
Suy ra: Tứ giác MEHB nội tiếp
b) Chứng minh MB=MA và EA⊥EH
Chứng minh MB=MA
- Tam giác MOA vuông tại A, do MA là tiếp tuyến tại A, nên MA⊥OA
- Tương tự, từ phần trên, tam giác MCB vuông tại B (vì BC là đường kính ⇒ ∠MCB=90∘)
→ Tam giác MOA và tam giác MOB vuông tại A và B, cùng chung cạnh huyền MO
⇒ MA=MB
Đpcm
Chứng minh EA⊥EH
Ta có:
- E nằm trên đường tròn, C là điểm đối xứng của B qua tâm O (vì BC là đường kính)
- EA nối từ E đến A, EH nối từ E đến chân đường vuông góc từ tâm O xuống AB
- Tứ giác MEHB nội tiếp ⇒ ∠BEH=∠BMH
- Mà MB=MA ⇒ tam giác AMB cân tại M
Suy ra các góc ∠BEH và ∠AEM đối đỉnh nhau qua đường trung trực, nên bằng nhau và tổng ∠AEH=90∘
✅ Suy ra: EA⊥EH
- a) MEHB là tứ giác nội tiếp
- b) MB=MA, và EA⊥EH
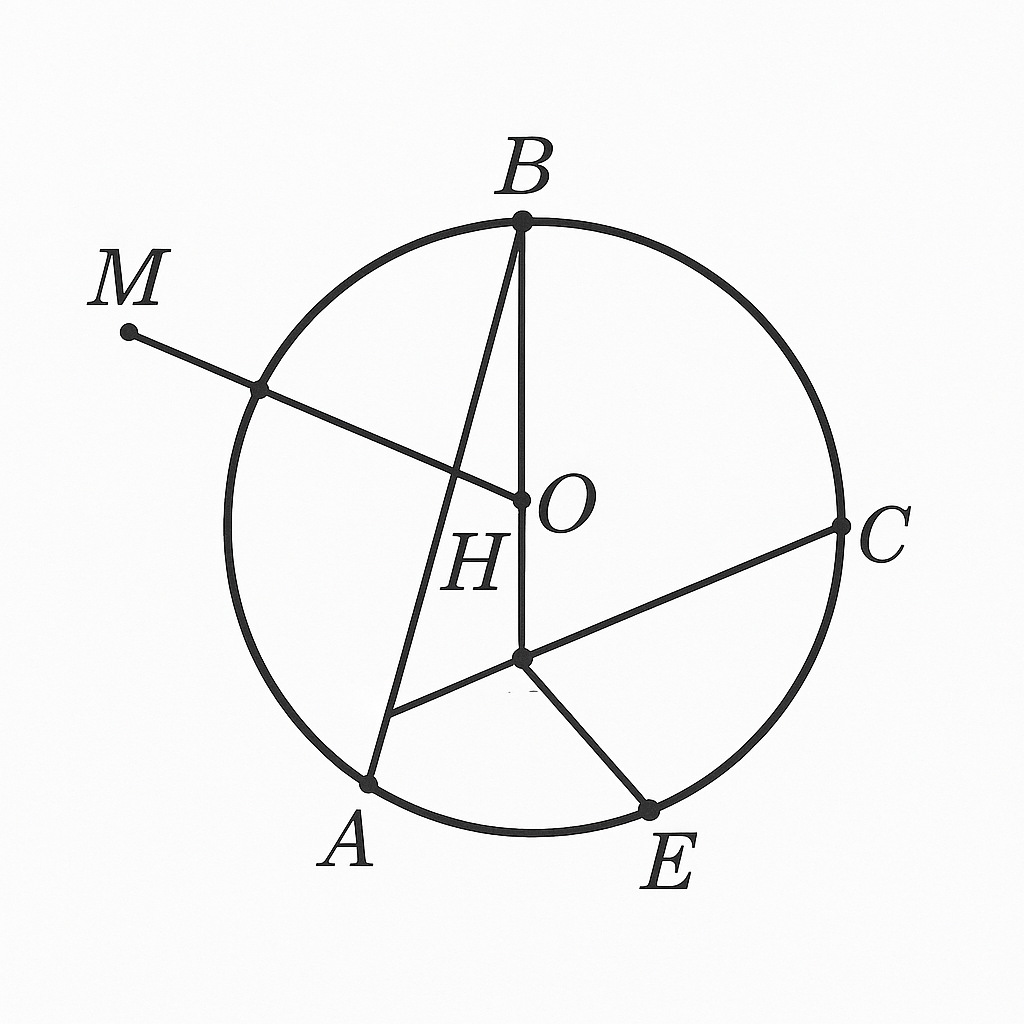
Do đó, ∠BEC = 90°
Tứ giác MEHB nội tiếp đường tròn đường kính MB
Chứng minh MB = MA:
=>
Quảng cáo
Câu hỏi hot cùng chủ đề
-
102077
-
Hỏi từ APP VIETJACK66986
-
55606
-
45978
-
40607
-
30793













