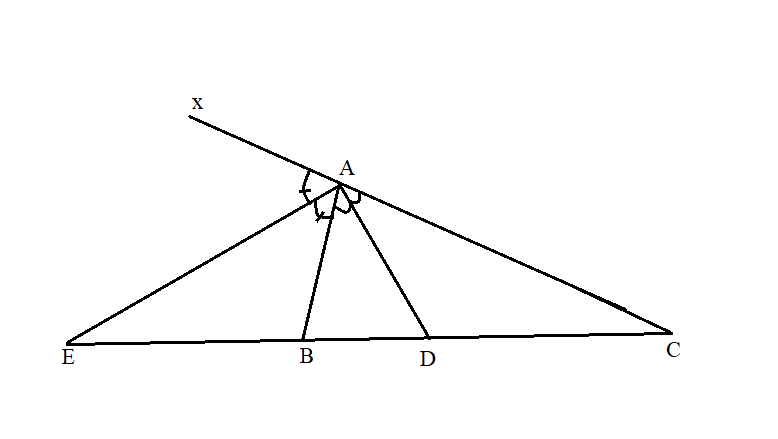
a,

Xét tam giác ABD có :

ˆB+ˆADB+ˆBAD=1800    (1)𝐵^+𝐴𝐷𝐵^+𝐵𝐴𝐷^=1800    (1)

Tương tự:

Xét tam giác ADC có :

ˆC+ˆADC+ˆCAD=1800   𝐶^+𝐴𝐷𝐶^+𝐶𝐴𝐷^=1800   (2)

Trừ lần lượt 2 vế của ( 1 )và  (2) ta được :

(ˆB+ˆADB+ˆBAD)−(ˆC+ˆADC+ˆCAD))=1800 −1800   ⇔ˆB−ˆC +ˆBAD−ˆCAD =ˆADC−ˆADB    (3)(𝐵^+𝐴𝐷𝐵^+𝐵𝐴𝐷^)-𝐶^+𝐴𝐷𝐶^+𝐶𝐴𝐷^)=1800 -1800   ⇔𝐵^-𝐶^ +𝐵𝐴𝐷^-𝐶𝐴𝐷^ =𝐴𝐷𝐶^-𝐴𝐷𝐵^    (3)

Do AD là tía phân giác của góc A nên:

ˆBAD=ˆDAC=ˆBAC2   (4)𝐵𝐴𝐷^=𝐷𝐴𝐶^=𝐵𝐴𝐶^2   (4)

Thay (4) vào (3) ta được:

ˆB−ˆC +0 =ˆADC−ˆADB hay ˆADC−ˆADB =ˆB−ˆC    (đccm)𝐵^-𝐶^ +0 =𝐴𝐷𝐶^-𝐴𝐷𝐵^ ℎ𝑎𝑦 𝐴𝐷𝐶^-𝐴𝐷𝐵^ =𝐵^-𝐶^    (đ𝑐𝑐𝑚)

b,

Ta có: 

ˆABE +ˆB =1800  (Do là 2 góc kề bù nhau)⇒ˆABE =180°−ˆB           (*)ABE^ +𝐵^ =1800  (𝐷𝑜 𝑙à 2 𝑔ó𝑐 𝑘ề 𝑏ù 𝑛ℎ𝑎𝑢)⇒𝐴𝐵𝐸^ =180°-𝐵^           (*)

Xét tam giác ABC có:

ˆBAC +ˆB+ˆC=180°⇒ˆBAC=180° −ˆB−ˆC   (5)BAC^ +𝐵^+𝐶^=180°⇒𝐵𝐴𝐶^=180° -𝐵^-𝐶^   5

Lại có:

ˆBAx+ˆBAC=180°⇒ˆBAx=180°−ˆBAC BAx^+𝐵𝐴𝐶^=180°⇒𝐵𝐴𝑥^=180°-𝐵𝐴𝐶^ 

Thay (5) vào ta được:

ˆBAx=180°−(180°−ˆB−ˆC) = ˆB +ˆC⇒ˆBAE=ˆBAx2=ˆB2+ˆC2  (**)   (Do AE là phân giác của ˆBAx)BAx^=180°-180°-𝐵^-𝐶^ = 𝐵^ +𝐶^⇒BAE^=BAx^2=B^2+C^2  (**)   (Do AE là phân giác của BAx^)

Xét tam giác AEB có:

ˆAEB +ˆABE+ˆBAE =180°AEB^ +𝐴𝐵𝐸^+𝐵𝐴𝐸^ =180°

Thay (*) và (**) vào ta được:

ˆC+ˆADC+ˆCAD=1800   𝐶^+𝐴𝐷𝐶^+𝐶𝐴𝐷^=180 độ