Chứng minh: OIKB nội tiếp
Quảng cáo
1 câu trả lời 620
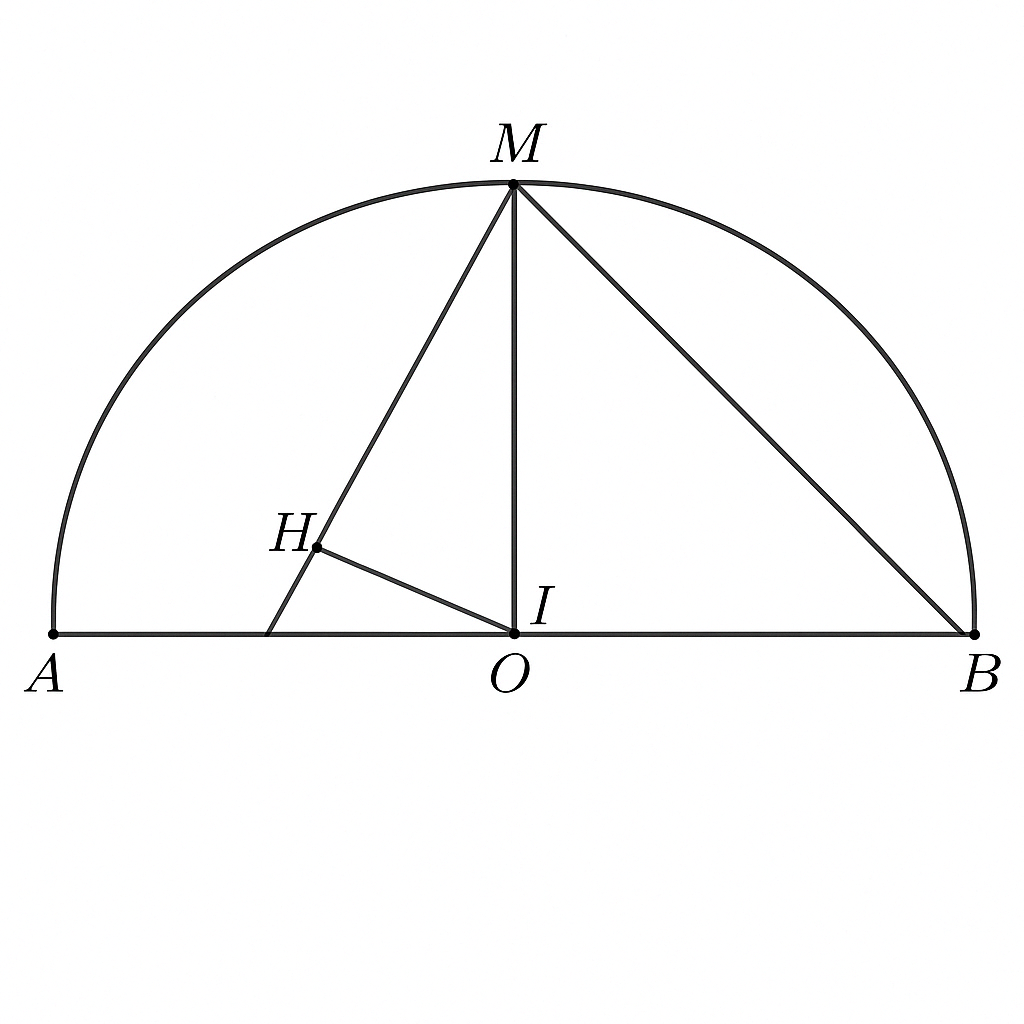
Tam giác AMB vuông tại M, do M là trung điểm cung AB trong nửa đường tròn đường kính AB.Tứ giác có 2 đường chéo cắt nhau tại I, với H là hình chiếu của M lên AK ⇒ Tạo góc vuông tại H
Tam giác AMB vuông tại M
Vì AB là đường kính và M nằm trên đường tròn ⇒ ∠AMB=90∘
Góc AKB là góc nội tiếp chắn cung AB
K nằm trên cung MB, nên ∠AKB là góc nội tiếp chắn cung AB
⇒ ∠AKB=∠AMB=90∘
H là hình chiếu vuông góc từ M lên AK ⇒ MH⊥AK
Tức là ∠MHA=90∘, do đó tứ giác MHIA có góc vuông tại H
Tam giác MOA cân tại O (vì OA=OB, và MO là trung tuyến)
Xét các tam giác và hình học phẳng tạo thành, từ đó suy ra:
∠OIK=∠OBK⇒(hai góc nội tiếp cùng chắn cung OK)
Tứ giác OIKB nội tiếp vì có:
∠OIK=∠OBK⇒OIKB là tứ giác nội tiếp
Quảng cáo
Câu hỏi hot cùng chủ đề
-
102042
-
Hỏi từ APP VIETJACK66834
-
55572
-
45855
-
40424
-
30538














