Cho đường tròn (O), điểm A nằm ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm).
a, Chứng minh rằng OA 1 MN
b, Vẽ đường kính NOC. Chứng minh rằng MC//AO.
c, Tính độ dài các cạnh của tam giác AMN biết AM=3cm, OA=5cm.
Quảng cáo
3 câu trả lời 2429
a) Ta có: AN = AM (tính chất tiếp tuyến)
Suy ra ∆AMN cân tại A
Mặt khác, OA là tia phân giác cũng là đường cao
Do đó OA ⊥ MN (đpcm).
b) Đặt H là giao điểm của MN và AO.
Ta có MH = HN (OA ⊥ MN nên H là trung điểm MN).
Mà CO = CN = R.
Suy ra OH là đường trung bình của ∆MNC.
Do đó OH // MC hay MC // OA (đpcm).
c) Ta có OM = ON = R nên ON = 3 cm.
Ta có: ON2 + AN2 = AO2 (theo định lý Py-ta-go)
Suy ra AN2 = AO2 – ON2= 52 – 32 = 25 – 9 = 16
⇒ AN = √16√1616 = 4 (cm)
Ta có: AO.HN = AN.NO (hệ thức lượng trong tam giác vuông).
Suy ra 5HN = 4 . 3 = 12 ⇒ HN = 125125125 = 2,4 (cm).
Ta có MN = 2HN = 2.2,4 = 4,8 (vì H là trung điểm MN).
Vậy AM = AN = 4 cm; MN = 4,8 cm.
ời giải
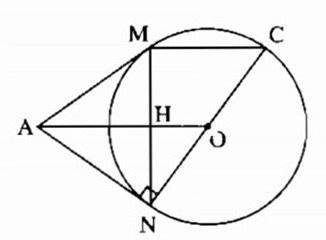
a) Ta có: AN = AM (tính chất tiếp tuyến)
Suy ra ∆AMN cân tại A
Mặt khác, OA là tia phân giác cũng là đường cao
Do đó OA ⊥ MN (đpcm).
b) Đặt H là giao điểm của MN và AO.
Ta có MH = HN (OA ⊥ MN nên H là trung điểm MN).
Mà CO = CN = R.
Suy ra OH là đường trung bình của ∆MNC.
Do đó OH // MC hay MC // OA (đpcm).
c) Ta có OM = ON = R nên ON = 3 cm.
Ta có: ON2 + AN2 = AO2 (theo định lý Py-ta-go)
Suy ra AN2 = AO2 – ON2= 52 – 32 = 25 – 9 = 16
⇒ AN = √16 = 4 (cm)
Ta có: AO.HN = AN.NO (hệ thức lượng trong tam giác vuông).
Suy ra 5HN = 4 . 3 = 12 ⇒ HN = 125 = 2,4 (cm).
Ta có MN = 2HN = 2.2,4 = 4,8 (vì H là trung điểm MN).
Vậy AM = AN = 4 cm; MN = 4,8 cm.
Đường thẳng AM và AN tiếp xúc với đường tròn (O) tại M và N.
OA là đường nối điểm A với tâm O.
Gọi I là trung điểm MN.
∠OMA = ∠ONA = 90° (định lý tiếp tuyến và bán kính).
OA đi qua I (định lý về dây cung và tiếp tuyến).
Vậy OA ⊥ MN.
b. Chứng minh MC // AO:
Vẽ đường kính NOC.
∠NMC = 90° và ∠NOC = 90°.
∠MNC = ∠AOC (định lý góc trong cùng phía).
Vậy MC // AO.
c. Tính độ dài các cạnh của ∆AMN:
AM = 3 cm.
OA = 5 cm.
OM^2 = OA^2 - AM^2 (định lý Pythagore)
OM^2 = 5^2 - 3^2
OM^2 = 25 - 9
OM = √16 = 4 cm
AN = AM = 3 cm (tiếp tuyến bằng nhau).
MN = 2OM = 2(4) = 8 cm.
Vậy các cạnh của ∆AMN là: AM = AN = 3 cm, MN = 8 cm.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103992
Đã trả lời bởi chuyên gia
103992 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69088
Đã trả lời bởi chuyên gia
69088 -
 Đã trả lời bởi chuyên gia
56995
Đã trả lời bởi chuyên gia
56995 -
 Đã trả lời bởi chuyên gia
47741
Đã trả lời bởi chuyên gia
47741 -
 Đã trả lời bởi chuyên gia
44729
Đã trả lời bởi chuyên gia
44729 -
 Đã trả lời bởi chuyên gia
37050
Đã trả lời bởi chuyên gia
37050 -
 Đã trả lời bởi chuyên gia
35840
Đã trả lời bởi chuyên gia
35840


