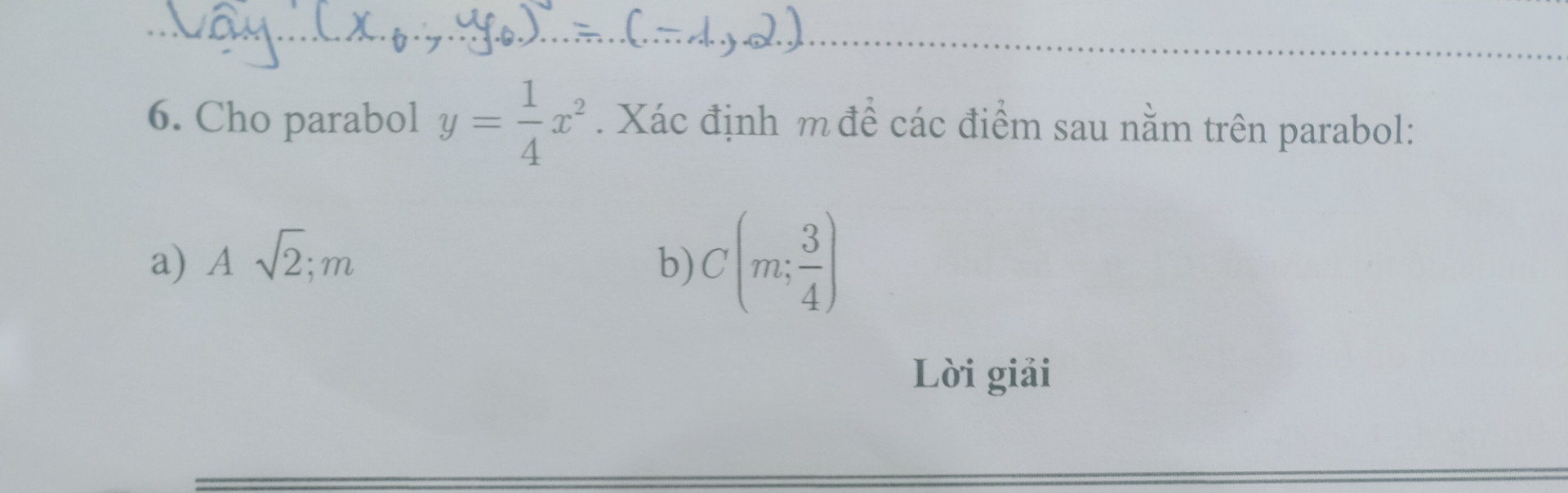Quảng cáo
4 câu trả lời 595
Để các điểm nằm trên parabol 4y=14x2, ta thay tọa độ của các điểm vào phương trình parabol và giải cho mm
a. Điểm A có tọa độ (√2,m)(2,m)
Ta thay x=√2x=2 vào phương trình parabol:
y=14(√2)2=14×2=12
Do đó, m=12m
b. Điểm C có tọa độ (m,34)
Ta thay y=34 vào phương trình parabol:
34=14m2
Nhân hai vế với 4:
3=m2
Giải phương trình m2=3, ta được:
m=±√3m=±3
#Kết luận:
a. m=12m=12
b. m=±√3
Để các điểm nằm trên parabol $4y = \frac{1}{4}x^2$, ta thay tọa độ của các điểm vào phương trình parabol và giải cho $m$
a. Điểm A có tọa độ $(\sqrt{2}, m)$
Ta thay $x = \sqrt{2}$ vào phương trình parabol:
$y = \frac{1}{4} (\sqrt{2})^2 = \frac{1}{4} \times 2 = \frac{1}{2}$
Do đó, m=12m = \frac{1}{2}.
b. Điểm C có tọa độ (m,34)(m, \frac{3}{4})
Ta thay $y = \frac{3}{4}$ vào phương trình parabol:
$\frac{3}{4} = \frac{1}{4} m^2$
Nhân hai vế với 4:
$3 = m^2$
Giải phương trình $m^2 = 3$, ta được:
$m = \pm \sqrt{3}$
#Kết luận:
- a. $m = \frac{1}{2}$
- b. $m = \pm \sqrt{3}$
a)
$m = \frac{1}{4}(\sqrt{2})^2 = \frac{1}{4}(2) = \frac{1}{2}$
Vậy $m = \frac{1}{2}$.
b)
$\frac{3}{4} = \frac{1}{4}m^2$
$3 = m^2$
$m = \pm \sqrt{3}$
Vậy $m = \sqrt{3}$ hoặc $m = -\sqrt{3}$.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103992
Đã trả lời bởi chuyên gia
103992 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69088
Đã trả lời bởi chuyên gia
69088 -
 Đã trả lời bởi chuyên gia
56995
Đã trả lời bởi chuyên gia
56995 -
 Đã trả lời bởi chuyên gia
47741
Đã trả lời bởi chuyên gia
47741 -
 Đã trả lời bởi chuyên gia
44729
Đã trả lời bởi chuyên gia
44729 -
 Đã trả lời bởi chuyên gia
37050
Đã trả lời bởi chuyên gia
37050 -
 Đã trả lời bởi chuyên gia
35840
Đã trả lời bởi chuyên gia
35840