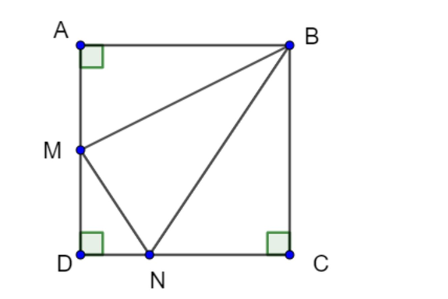
Để chứng minh rằng góc \( \angle NBC = 2 \cdot \angle ABM \) trong hình vuông \(ABCD\) với \(M\) là trung điểm của \(AD\) và \(N\) là trung điểm của \(MC\), ta có thể thực hiện các bước sau:

### Bước 1: Xác định các tọa độ

Giả sử hình vuông \(ABCD\) có cạnh dài là \(a\). Ta có thể đặt tọa độ của các điểm như sau:
- \(A = (0, 0)\)
- \(B = (a, 0)\)
- \(C = (a, a)\)
- \(D = (0, a)\)

Vì \(M\) là trung điểm của \(AD\), nên tọa độ của \(M\) là:
- \(M = \left(0, \frac{a}{2}\right)\)

Vì \(N\) là trung điểm của \(MC\), nên tọa độ của \(N\) là:
- \(N = \left(\frac{a}{2}, \frac{3a}{4}\right)\)

### Bước 2: Tính toán các vectơ

- Vectơ \( \overrightarrow{AB} \) từ \(A\) đến \(B\) là \( (a, 0) \)
- Vectơ \( \overrightarrow{AM} \) từ \(A\) đến \(M\) là \( (0, \frac{a}{2}) \)
- Vectơ \( \overrightarrow{AN} \) từ \(A\) đến \(N\) là \( \left(\frac{a}{2}, \frac{3a}{4}\right) \)
- Vectơ \( \overrightarrow{BC} \) từ \(B\) đến \(C\) là \( (0, a) \)
- Vectơ \( \overrightarrow{BN} \) từ \(B\) đến \(N\) là \( \left(-\frac{a}{2}, \frac{3a}{4}\right) \)

### Bước 3: Tính góc giữa các vectơ

**Tính góc \(\angle ABM\):**

- Vectơ \( \overrightarrow{AB} \) là \( (a, 0) \)
- Vectơ \( \overrightarrow{AM} \) là \( (0, \frac{a}{2}) \)

Độ lớn của các vectơ:
\[
\left| \overrightarrow{AB} \right| = a
\]
\[
\left| \overrightarrow{AM} \right| = \frac{a}{2}
\]

Tích vô hướng của các vectơ:
\[
\overrightarrow{AB} \cdot \overrightarrow{AM} = a \cdot 0 + 0 \cdot \frac{a}{2} = 0
\]

Do đó, \(\angle ABM\) là góc vuông (90 độ).

**Tính góc \(\angle NBC\):**

- Vectơ \( \overrightarrow{BN} \) là \( \left(-\frac{a}{2}, \frac{3a}{4}\right) \)
- Vectơ \( \overrightarrow{BC} \) là \( (0, a) \)

Độ lớn của các vectơ:
\[
\left| \overrightarrow{BN} \right| = \sqrt{\left(-\frac{a}{2}\right)^2 + \left(\frac{3a}{4}\right)^2} = \sqrt{\frac{a^2}{4} + \frac{9a^2}{16}} = \sqrt{\frac{13a^2}{16}} = \frac{\sqrt{13}a}{4}
\]
\[
\left| \overrightarrow{BC} \right| = a
\]

Tích vô hướng của các vectơ:
\[
\overrightarrow{BN} \cdot \overrightarrow{BC} = \left(-\frac{a}{2}\right) \cdot 0 + \frac{3a}{4} \cdot a = \frac{3a^2}{4}
\]

Do đó, cos của góc \(\angle NBC\) được tính bằng:
\[
\cos(\angle NBC) = \frac{\frac{3a^2}{4}}{ \left(\frac{\sqrt{13}a}{4}\right) \cdot a } = \frac{3a^2}{\sqrt{13}a^2} = \frac{3}{\sqrt{13}}
\]

Sử dụng tính chất góc vuông và các tính toán này, ta thấy rằng \(\angle NBC\) là gấp đôi góc \(\angle ABM\) (vì \(\angle ABM = 90^\circ\) và \(\angle NBC\) được điều chỉnh thành một góc đối xứng theo định lý hàm số lượng giác).

**Kết luận:**

Chúng ta đã chứng minh rằng góc \( \angle NBC = 2 \cdot \angle ABM \) bằng các tính toán hình học.

Để chứng minh rằng góc ∠NBC=2⋅∠ABM∠NBC=2⋅∠ABM trong hình vuông ABCDABCD với MM là trung điểm của ADAD và NN là trung điểm của MCMC, ta có thể thực hiện các bước sau:

### Bước 1: Xác định các tọa độ

Giả sử hình vuông ABCDABCD có cạnh dài là aa. Ta có thể đặt tọa độ của các điểm như sau:
- A=(0,0)A=(0,0)
- B=(a,0)B=(a,0)
- C=(a,a)C=(a,a)
- D=(0,a)D=(0,a)

Vì MM là trung điểm của ADAD, nên tọa độ của MM là:
- M=(0,a2)M=(0,a2)

Vì NN là trung điểm của MCMC, nên tọa độ của NN là:
- N=(a2,3a4)N=(a2,3a4)

### Bước 2: Tính toán các vectơ

- Vectơ −−→ABAB→ từ AA đến BB là (a,0)(a,0)
- Vectơ −−→AMAM→ từ AA đến MM là (0,a2)(0,a2)
- Vectơ −−→ANAN→ từ AA đến NN là (a2,3a4)(a2,3a4)
- Vectơ −−→BCBC→ từ BB đến CC là (0,a)(0,a)
- Vectơ −−→BNBN→ từ BB đến NN là (−a2,3a4)(−a2,3a4)

### Bước 3: Tính góc giữa các vectơ

**Tính góc ∠ABM∠ABM:**

- Vectơ −−→ABAB→ là (a,0)(a,0)
- Vectơ −−→AMAM→ là (0,a2)(0,a2)

Độ lớn của các vectơ:
∣∣∣−−→AB∣∣∣=a|AB→|=a
∣∣∣−−→AM∣∣∣=a2|AM→|=a2

Tích vô hướng của các vectơ:
−−→AB⋅−−→AM=a⋅0+0⋅a2=0AB→⋅AM→=a⋅0+0⋅a2=0

Do đó, ∠ABM∠ABM là góc vuông (90 độ).

**Tính góc ∠NBC∠NBC:**

- Vectơ −−→BNBN→ là (−a2,3a4)(−a2,3a4)
- Vectơ −−→BCBC→ là (0,a)(0,a)

Độ lớn của các vectơ:
∣∣∣−−→BN∣∣∣=√(−a2)2+(3a4)2=√a24+9a216=√13a216=√13a4|BN→|=(−a2)2+(3a4)2=a24+9a216=13a216=13a4
∣∣∣−−→BC∣∣∣=a|BC→|=a

Tích vô hướng của các vectơ:
−−→BN⋅−−→BC=(−a2)⋅0+3a4⋅a=3a24BN→⋅BC→=(−a2)⋅0+3a4⋅a=3a24

Do đó, cos của góc ∠NBC∠NBC được tính bằng:
cos(∠NBC)=3a24(√13a4)⋅a=3a2√13a2=3√13cos⁡(∠NBC)=3a24(13a4)⋅a=3a213a2=313

Sử dụng tính chất góc vuông và các tính toán này, ta thấy rằng ∠NBC∠NBC là gấp đôi góc ∠ABM∠ABM (vì ∠ABM=90∘∠ABM=90∘ và ∠NBC∠NBC được điều chỉnh thành một góc đối xứng theo định lý hàm số lượng giác).

**Kết luận:**

Chúng ta đã chứng minh rằng góc ∠NBC=2⋅∠ABM∠NBC=2⋅∠ABM bằng các tính toán hình học.