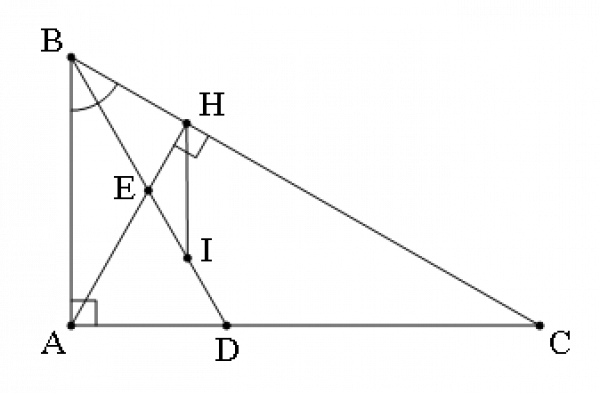
Cho tam giác vuông tại A, đường cao AH. Đường phân giác của góc cắt AC tại D và cắt AH tại E.
a. Chứng minh: đồng dạng và
b. Biết AB = 9cm, BC = 15cm. Tính DC và AD.
Gọi I là trung điểm của ED. Chứng minh :
Quảng cáo
9 câu trả lời 40458
a. Chứng minh: đồng dạng và
Vì AH là đường cao (gt) nên
Xét và có:
chung
(hai cặp cạnh tương ứng tỉ lệ)
b. Biết AB = 9cm, BC = 15cm. Tính DC và AD.
Xét vuông tại A, ta có:
(định lí Pitago)
Mà AB = 9cm, BC = 15cm nên ta được:
Gọi độ dài AD là x (cm). Mà
Ta được: DC = 12 – x (cm)
Vì BD là tia phân giác của góc (gt) nên ta có:
Vậy độ dài đoạn AD = 4,5 cm, DC = 12-4,5 = 7,5 cm.
c. Gọi I là trung điểm của ED. Chứng minh :
Chứng minh :
Chứng minh:
Mà (vì )
a. Chứng minh: đồng dạng và
Vì AH là đường cao (gt) nên
Xét và có:
chung
(hai cặp cạnh tương ứng tỉ lệ)
b. Biết AB = 9cm, BC = 15cm. Tính DC và AD.
Xét vuông tại A, ta có:
(định lí Pitago)
Mà AB = 9cm, BC = 15cm nên ta được:
Gọi độ dài AD là x (cm). Mà
Ta được: DC = 12 – x (cm)
Vì BD là tia phân giác của góc (gt) nên ta có:
Vậy độ dài đoạn AD = 4,5 cm, DC = 12-4,5 = 7,5 cm.
c. Gọi I là trung điểm của ED. Chứng minh :
Chứng minh :
Chứng minh:
Mà (vì )
Chứng minh: ΔABCΔABC đồng dạng ΔHBAΔHBA và AB2=BC.BHAB2=BC.BH
Vì AH là đường cao (gt) nên
Xét ΔABCΔABC và ΔHBAΔHBA có:
ˆBAC=ˆBHA=90°BAC^=BHA^=90°
ˆBB^ chung
⇒ΔABC~ΔHBA(g.g)⇒ΔABC~ΔHBA(g.g)
⇒ABHB=BCBA⇒ABHB=BCBA (hai cặp cạnh tương ứng tỉ lệ)
⇔AB2=BC.BH⇔AB2=BC.BH
b. Biết AB = 9cm, BC = 15cm. Tính DC và AD.
Xét ΔABCΔABC vuông tại A, ta có:
AB2+AC2=BC2AB2+AC2=BC2 (định lí Pitago)
Mà AB = 9cm, BC = 15cm nên ta được:
AC2=152−92=225−81=144AC2=152-92=225-81=144
⇒AC=12cm⇒AC=12cm
Gọi độ dài AD là x (cm). Mà AD + DC = 12(cm)AD + DC = 12(cm)
Ta được: DC = 12 – x (cm)
Vì BD là tia phân giác của góc ˆBB^ (gt) nên ta có:
⇔x9=12−x15⇔x9=12-x15
⇔15x=108−9x⇔15x=108-9x
⇔24x=108⇔24x=108
⇔x=4,5⇔x=4,5
Vậy độ dài đoạn AD = 4,5 cm, DC = 12-4,5 = 7,5 cm.
c. Gọi I là trung điểm của ED. Chứng minh : ˆBIH=ˆACBBIH^=ACB^
Chứng minh : ΔBEH~ΔAEI(g.g)ΔBEH~ΔAEI(g.g)
Chứng minh: ΔAEB~ΔIEH(c.g.c)⇒ˆBAE=ˆEIHΔAEB~ΔIEH(c.g.c)⇒BAE^=EIH^
Mà ˆBAE=ˆACBBAE^=ACB^ (vì ΔABC~ΔHBA(g.g)ΔABC~ΔHBA(g.g) )
⇒ˆBIH=ˆACB
Chứng minh: ΔABCΔABC đồng dạng ΔHBAΔHBA và AB2=BC.BHAB2=BC.BH
Vì AH là đường cao (gt) nên
Xét ΔABCΔABC và ΔHBAΔHBA có:
ˆBAC=ˆBHA=90°BAC^=BHA^=90°
ˆBB^ chung
⇒ΔABC~ΔHBA(g.g)⇒ΔABC~ΔHBA(g.g)
⇒ABHB=BCBA⇒ABHB=BCBA (hai cặp cạnh tương ứng tỉ lệ)
⇔AB2=BC.BH⇔AB2=BC.BH
b. Biết AB = 9cm, BC = 15cm. Tính DC và AD.
Xét ΔABCΔABC vuông tại A, ta có:
AB2+AC2=BC2AB2+AC2=BC2 (định lí Pitago)
Mà AB = 9cm, BC = 15cm nên ta được:
AC2=152−92=225−81=144AC2=152-92=225-81=144
⇒AC=12cm⇒AC=12cm
Gọi độ dài AD là x (cm). Mà AD + DC = 12(cm)AD + DC = 12(cm)
Ta được: DC = 12 – x (cm)
Vì BD là tia phân giác của góc ˆBB^ (gt) nên ta có:
⇔x9=12−x15⇔x9=12-x15
⇔15x=108−9x⇔15x=108-9x
⇔24x=108⇔24x=108
⇔x=4,5⇔x=4,5
Vậy độ dài đoạn AD = 4,5 cm, DC = 12-4,5 = 7,5 cm.
c. Gọi I là trung điểm của ED. Chứng minh : ˆBIH=ˆACBBIH^=ACB^
Chứng minh : ΔBEH~ΔAEI(g.g)ΔBEH~ΔAEI(g.g)
Chứng minh: ΔAEB~ΔIEH(c.g.c)⇒ˆBAE=ˆEIHΔAEB~ΔIEH(c.g.c)⇒BAE^=EIH^
Mà ˆBAE=ˆACBBAE^=ACB^ (vì ΔABC~ΔHBA(g.g)ΔABC~ΔHBA(g.g) )
⇒ˆBIH=ˆACB
Chứng minh: ΔABCΔABC đồng dạng ΔHBAΔHBA và AB2=BC.BHAB2=BC.BH
Vì AH là đường cao (gt) nên
Xét ΔABCΔABC và ΔHBAΔHBA có:
ˆBAC=ˆBHA=90°BAC^=BHA^=90°
ˆBB^ chung
⇒ΔABC~ΔHBA(g.g)⇒ΔABC~ΔHBA(g.g)
⇒ABHB=BCBA⇒ABHB=BCBA (hai cặp cạnh tương ứng tỉ lệ)
⇔AB2=BC.BH⇔AB2=BC.BH
b. Biết AB = 9cm, BC = 15cm. Tính DC và AD.
Xét ΔABCΔABC vuông tại A, ta có:
AB2+AC2=BC2AB2+AC2=BC2 (định lí Pitago)
Mà AB = 9cm, BC = 15cm nên ta được:
AC2=152−92=225−81=144AC2=152-92=225-81=144
⇒AC=12cm⇒AC=12cm
Gọi độ dài AD là x (cm). Mà AD + DC = 12(cm)AD + DC = 12(cm)
Ta được: DC = 12 – x (cm)
Vì BD là tia phân giác của góc ˆBB^ (gt) nên ta có:
⇔x9=12−x15⇔x9=12-x15
⇔15x=108−9x⇔15x=108-9x
⇔24x=108⇔24x=108
⇔x=4,5⇔x=4,5
Vậy độ dài đoạn AD = 4,5 cm, DC = 12-4,5 = 7,5 cm.
c. Gọi I là trung điểm của ED. Chứng minh : ˆBIH=ˆACBBIH^=ACB^
Chứng minh : ΔBEH~ΔAEI(g.g)ΔBEH~ΔAEI(g.g)
Chứng minh: ΔAEB~ΔIEH(c.g.c)⇒ˆBAE=ˆEIHΔAEB~ΔIEH(c.g.c)⇒BAE^=EIH^
Mà ˆBAE=ˆACBBAE^=ACB^ (vì ΔABC~ΔHBA(g.g)ΔABC~ΔHBA(g.g) )
⇒ˆBIH=ˆACB
a) Liệt kê các kết quả có thể thực nghiệm trên
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
108775
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69580
Đã trả lời bởi chuyên gia
69580 -
 Đã trả lời bởi chuyên gia
53348
Đã trả lời bởi chuyên gia
53348 -
 Đã trả lời bởi chuyên gia
47786
Đã trả lời bởi chuyên gia
47786 -
 Đã trả lời bởi chuyên gia
45963
Đã trả lời bởi chuyên gia
45963 -
 Đã trả lời bởi chuyên gia
45824
Đã trả lời bởi chuyên gia
45824 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
39522
Đã trả lời bởi chuyên gia
39522 -
 Đã trả lời bởi chuyên gia
38637
Đã trả lời bởi chuyên gia
38637


