Cho tam giác ABC vuông tại A có AB =12cm, AC=16cm, vẽ đường cao AH
a, Chứng minh: Tam giác HBA đồng dạng với tam giác ABC
b, Tính BC AH
c, Trong tam giác ABC kẻ phân giác AD (D thuộc BC). Trong tam giác ADB kẻ phân giác DE (E thuộc AB). Trong tam giác ADC kẻ phân giác DF(F thuộc AC). Chứng minh:
Quảng cáo
20 câu trả lời 108945
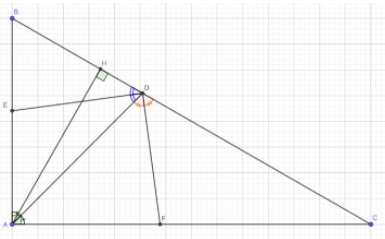
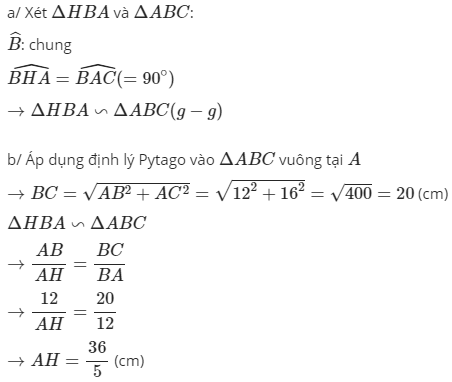

Cho tam giác ABC vuông tại A có AB =12cm, AC=16cm, vẽ đường cao AH
a, Chứng minh: Tam giác HBA đồng dạng với tam giác ABC
b, Tính BC AH
c, Trong tam giác ABC kẻ phân giác AD (D thuộc BC). Trong tam giác ADB kẻ phân giác DE (E thuộc AB). Trong tam giác ADC kẻ phân giác DF(F thuộc AC). Chứng minh:
Cho tam giác ABC vuông tại A có AB =12cm, AC=16cm, vẽ đường cao AH
a, Chứng minh: Tam giác HBA đồng dạng với tam giác ABC
b, Tính BC AH
c, Trong tam giác ABC kẻ phân giác AD (D thuộc BC). Trong tam giác ADB kẻ phân giác DE (E thuộc AB). Trong tam giác ADC kẻ phân giác DF(F thuộc AC). Chứng minh:
a) Chứng minh: Tam giác HBA đồng dạng với tam giác ABC
Ta có tam giác ABC vuông tại A, với đường cao AH. Khi đó, góc HAB và góc BAC là góc vuông chung, do đó, ta có:
góc HAB = góc BAC (góc vuông chung)
góc HBA = góc CBA (góc vuông chung)
Vậy, theo góc-góc đồng dạng, ta có tam giác HBA đồng dạng với tam giác ABC.
b) Tính BC/AH
Theo định lý Pythagoras trong tam giác vuông ABC, ta có:
BC² = AB² + AC²
BC² = 12² + 16²
BC² = 144 + 256
BC² = 400
BC = √400
BC = 20 cm
Vì AH là đường cao của tam giác ABC, nên AH cũng là đường cao của tam giác HBA. Do tam giác HBA đồng dạng với tam giác ABC, nên tỉ lệ giữa các cạnh của hai tam giác này là như nhau. Ta có:
BC/AH = AB/HA
20/AH = 12/AH
20 = 12
AH = 12 cm
Vậy, BC/AH = 20/12 = 5/3.
c) Chứng minh: Tam giác EAB đồng dạng với tam giác FCA
Ta cần chứng minh tam giác EAB đồng dạng với tam giác FCA. Để chứng minh điều này, ta cần chứng minh tỉ lệ giữa các cạnh của hai tam giác này.
Theo định lí phân giác trong tam giác, ta có:
AE/EB = AD/DB
AF/FC = AD/DC
Vì AD là đường phân giác của góc BAC, nên ta có:
AD/DB = AC/BC
AD/DC = AB/BC
Kết hợp với các công thức trên, ta có:
AE/EB = AF/FC
AB/BC = AC/BC
Từ đó, ta suy ra:
AE/EB = AF/FC = AB/BC = AC/BC
Vậy, tam giác EAB đồng dạng với tam giác FCA theo tỉ lệ AE/EB = AF/FC = AB/BC = AC/BC = 1.
a) Chứng minh: Tam giác HBA đồng dạng với tam giác ABC
Ta có tam giác ABC vuông tại A, với đường cao AH. Khi đó, góc HAB và góc BAC là góc vuông chung, do đó, ta có:
góc HAB = góc BAC (góc vuông chung)
góc HBA = góc CBA (góc vuông chung)
Vậy, theo góc-góc đồng dạng, ta có tam giác HBA đồng dạng với tam giác ABC.
b) Tính BC/AH
Theo định lý Pythagoras trong tam giác vuông ABC, ta có:
BC² = AB² + AC²
BC² = 12² + 16²
BC² = 144 + 256
BC² = 400
BC = √400
BC = 20 cm
Vì AH là đường cao của tam giác ABC, nên AH cũng là đường cao của tam giác HBA. Do tam giác HBA đồng dạng với tam giác ABC, nên tỉ lệ giữa các cạnh của hai tam giác này là như nhau. Ta có:
BC/AH = AB/HA
20/AH = 12/AH
20 = 12
AH = 12 cm
Vậy, BC/AH = 20/12 = 5/3.
c) Chứng minh: Tam giác EAB đồng dạng với tam giác FCA
Ta cần chứng minh tam giác EAB đồng dạng với tam giác FCA. Để chứng minh điều này, ta cần chứng minh tỉ lệ giữa các cạnh của hai tam giác này.
Theo định lí phân giác trong tam giác, ta có:
AE/EB = AD/DB
AF/FC = AD/DC
Vì AD là đường phân giác của góc BAC, nên ta có:
AD/DB = AC/BC
AD/DC = AB/BC
Kết hợp với các công thức trên, ta có:
AE/EB = AF/FC
AB/BC = AC/BC
Từ đó, ta suy ra:
AE/EB = AF/FC = AB/BC = AC/BC
Vậy, tam giác EAB đồng dạng với tam giác FCA theo tỉ lệ AE/EB = AF/FC = AB/BC = AC/BC = 1
a) Chứng minh: Tam giác HBA đồng dạng với tam giác ABC
Ta có tam giác ABC vuông tại A, với đường cao AH. Khi đó, góc HAB và góc BAC là góc vuông chung, do đó, ta có:
góc HAB = góc BAC (góc vuông chung)
góc HBA = góc CBA (góc vuông chung)
Vậy, theo góc-góc đồng dạng, ta có tam giác HBA đồng dạng với tam giác ABC.
b) Tính BC/AH
Theo định lý Pythagoras trong tam giác vuông ABC, ta có:
BC² = AB² + AC²
BC² = 12² + 16²
BC² = 144 + 256
BC² = 400
BC = √400
BC = 20 cm
Vì AH là đường cao của tam giác ABC, nên AH cũng là đường cao của tam giác HBA. Do tam giác HBA đồng dạng với tam giác ABC, nên tỉ lệ giữa các cạnh của hai tam giác này là như nhau. Ta có:
BC/AH = AB/HA
20/AH = 12/AH
20 = 12
AH = 12 cm
Vậy, BC/AH = 20/12 = 5/3.
c) Chứng minh: Tam giác EAB đồng dạng với tam giác FCA
Ta cần chứng minh tam giác EAB đồng dạng với tam giác FCA. Để chứng minh điều này, ta cần chứng minh tỉ lệ giữa các cạnh của hai tam giác này.
Theo định lí phân giác trong tam giác, ta có:
AE/EB = AD/DB
AF/FC = AD/DC
Vì AD là đường phân giác của góc BAC, nên ta có:
AD/DB = AC/BC
AD/DC = AB/BC
Kết hợp với các công thức trên, ta có:
AE/EB = AF/FC
AB/BC = AC/BC
Từ đó, ta suy ra:
AE/EB = AF/FC = AB/BC = AC/BC
Vậy, tam giác EAB đồng dạng với tam giác FCA theo tỉ lệ AE/EB = AF/FC = AB/BC = AC/BC = 1
a.
Xét ΔHBAΔHBA và ΔABCΔABC có:
góc B chung
góc H = A = 90o
Do đó: ΔHBA∼ABCΔHBA∼ABC ( g.g)
b.
Tam giác ABC vuông tại A
=> BC2 = AB2 + AC2
=> BC2 = 122 + 162
=> BC = 20 ( cm)
Tam giác HBA ~ ABC
=> AHAC=ABBC⇒AH=AC.ABBC=12.1620=9,6AHAC=ABBC⇒AH=AC.ABBC=12.1620=9,6
Tam giác HBA vuông tại H
=> AB2 = AH2 + BH2
=> BH2 = AB2 - AH2
=> BH2 = 122 - 9,62
=> BH2 = 7,2 ( cm)
c)
Ta có: AD là đường phân giác của góc BAC
=> BDCD=ABAC=1216=34BDCD=ABAC=1216=34
=> BD3=CD4=BD+CD3+4=207BD3=CD4=BD+CD3+4=207
Suy ra:
BD=20.37=607cm
CD=20.47=807cm
d.
Ta có: MN // BC
=> Tứ giác BMNC là hình thang
Xét tam giác AMK và tam giác CBA có:
góc K = A = 90o
góc AMK = CBA ( đồng vị)
Do đó: tam giác AMK~CBA ( g.g)
=> AMCB=AKCA⇒AM=CB.AKCA=20.3,616=4,5cm
Xét tam giác ABC có: MN // BC
=> AMAB=MNBC⇒MN=AM.BCAB=4,5.2012=7,5cm
Ta có: AK + KH = AH
=> KH = 9,6 - 3,6 = 6 (cm)
Diện tích hình thang BMNC là:
12.(MN+BC).KH
=12(7,5+20).6
= 82,5 cm2
- là góc chung.
- (do là đường cao, vuông tại ).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69580
Đã trả lời bởi chuyên gia
69580 -
 Đã trả lời bởi chuyên gia
53348
Đã trả lời bởi chuyên gia
53348 -
 Đã trả lời bởi chuyên gia
47786
Đã trả lời bởi chuyên gia
47786 -
 Đã trả lời bởi chuyên gia
45963
Đã trả lời bởi chuyên gia
45963 -
 Đã trả lời bởi chuyên gia
45824
Đã trả lời bởi chuyên gia
45824 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
39522
Đã trả lời bởi chuyên gia
39522 -
 Đã trả lời bởi chuyên gia
38637
Đã trả lời bởi chuyên gia
38637


