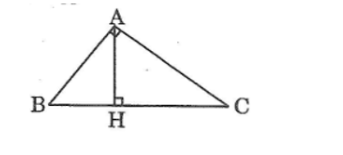
Đề bài cho ta một tam giác vuông \( ABC \) tại \( A \), và đường cao \( AH \) từ \( A \) xuống \( BC \) có độ dài \( AH = 1 \). Đồng thời, \( BH = 1 \) và \( CH = 2 \).

### Bước 1: Tính độ dài \( AB \) và \( AC \)

Vì \( AH \) là đường cao từ \( A \) xuống \( BC \), ta có:

\[ BH = 1, \quad CH = 2 \]

\( BH + CH = BC = b \):

\[ b = BH + CH = 1 + 2 = 3 \]

Vậy, \( BC = 3 \).

Do đó, \( AB \) và \( AC \) là các cạnh của tam giác vuông \( ABC \), ta có:

\[ AB = AH = 1 \]
\[ AC = \sqrt{BC^2 - AH^2} = \sqrt{3^2 - 1^2} = \sqrt{9 - 1} = \sqrt{8} = 2\sqrt{2} \]

### Bước 2: Tính \( \sin B \) và \( \sin C \)

Vì \( \triangle ABC \) là tam giác vuông tại \( A \):

- \( \angle B \) là góc ở \( B \),
- \( \angle C \) là góc ở \( C \).

\[ \sin B = \frac{\text{Đối diện } \angle B}{\text{Cạnh huyền}} = \frac{AC}{BC} = \frac{2\sqrt{2}}{3} \]

\[ \sin C = \frac{\text{Đối diện } \angle C}{\text{Cạnh huyền}} = \frac{AB}{BC} = \frac{1}{3} \]

Vậy,

\[ \sin B = \frac{2\sqrt{2}}{3} \]
\[ \sin C = \frac{1}{3} \]

### Kết quả cuối cùng:
- Độ dài \( AB = 1 \), \( AC = 2\sqrt{2} \).
- \( \sin B = \frac{2\sqrt{2}}{3} \), \( \sin C = \frac{1}{3} \).

Cho tam giác vuông ABC vuông tại A , đường cao AH , đường cao BH = 1 , CH = 2 .
Tính AB , AC
Tính sin B , sin C .
Trả Lời Theo dõi
 Hỏi chi tiết
 
QUẢNG CÁO

 
 
Pause 00:00
00:05
01:31
Mute
 

0 câu trả lời 3
Trả lời
Vũ Cương đang đợi giúp đỡ của bạn. Viết câu trả lời

Thêm câu trả lời sẽ cộng điểm.
QUẢNG CÁO

 
CÂU HỎI HOT CÙNG CHỦ ĐỀ
 
ad
Cho nửa đường tròn tâm O đường kính AB, C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I, K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D.

Chứng minh :

a) Các tứ giác ACMD, BCKM nội tiếp đường tròn

b) CK.CD=CA.CB

c) Gọi N là giao điểm của AD và đường tròn O chứng minh B, K, N thẳng hàng

d) Tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định khi K di động trên đoạn thẳng CI
Trả lời (33) Xem đáp án »
 3 93023
Hỏi từ APP VIETJACKHai người cùng làm chung một công việc trong 12/5 giờ thì xong nếu mỗi người làm một mình thì thời gian người thứ nhất hoàn thành công việc ít hơn người thứ hai là 2 giờ hỏi nếu làm một mình thì mỗi người phải làm trong bao nhiêu thời gian để trong công việc ?
Trả lời (8) Xem đáp án »
 3 57125
Cho đường trong (O, R) và đường thẳng d không qua O cắt đường tròn tại hai điểm A, B. Lấy một điểm M trên tia đối của tia BA  kẻ hai tiếp tuyến MC, MD với đường tròn (C, D là các tiếp điểm). Gọi H là trung điểm của AB.

    1) Chứng minh rằng các điểm M, D, O, H cùng nằm trên một đường tròn.

    2) Đoạn OM cắt đường tròn tại I. Chứng minh rằng I là tâm đường tròn nội tiếp tam giác MCD.

    3) Đường thẳng qua O, vuông góc với OM cắt các tia MC, MD thứ tự tại P và Q. Tìm vị trí của điểm M trên d sao cho diện tích tam giác MPQ bé nhất. 
Trả lời (5) Xem đáp án »
 47342
 
ad
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H.

1, Chứng minh tứ giác BDHF là tứ giác nội tiếp

2, Chứng minh tứ giác BFEC là tứ giác nội tiếp

3, Tìm thêm các tứ giác nội tiếp

4, Chứng minh FC là phân giác của góc DFE

5, Chứng minh H là tâm đường tròn nội tiếp Δ DEF

6, Lấy K đối xứng với H qua BC. Chứng minh K thuộc đường tròn tâm O

7, Chứng minh OA vuông góc với FE

8, Gọi Ià trung điểm của BC. Chứng minh AH = 2OI
Trả lời (24) Xem đáp án »
 13 33659
Theo kế hoạch hai tổ được giao sản xuất 600 sản phẩm trong một thời gian đã định. Do cải tiến kĩ thuật nên tổ I đã sản xuất vượt mức kế hoạch 18% và tổ II sản xuất vượt mức kế hoạch 21%. Vì vậy trong cùng thời gian quy định hai tổ đã hoàn thành vượt mức 120 sản phẩm. Tính số sản phẩm được giao của mỗi tổ theo kế hoạch.
Trả lời (4) Xem đáp án »
 1 32760
Hỏi từ APP VIETJACKCho biểu thức P = (1/(x - sqrt(x)) + 1/(sqrt(x) - 1)); (sqrt(x) + 1)/((sqrt(x) - 1) ^ 2)
a) Rút gọn biểu thức P. (với 0 <x ne1)
b) Tìm giá trị lớn nhất của biểu thức Q = P - 9sqrt(x) + 2021
Trả lời (4) Xem đáp án »
 29817
 
ad
a,cho cos a=2/3.hãy tính sin a,tận a,cot a
Trả lời (6) Xem đáp án »
 4 27608
Rút gọn các biểu thức: √4−2√3−√34-23-3
Trả lời (8) Xem đáp án »
 2 23371
Chọn đáp án đúng. Căn bậc hai số học của (−3)2(-3)2 là:

A. −3                    

B. 3                      

C. −81                  

D. 81
Trả lời (55) Xem đáp án »
 1 23163
Hỏi từ APP VIETJACKCho hàm số y=-2x+3 có đồ thị là (d1) và hàm số y=x-1 có đồ thị là (d2) a)Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ b)Tìm tọa độ giao điểm của (d1) và (d2) bằng phép tính c) Vẽ phương trình đường thẳng (d3) đi qua điểm A(-2;1) và song song với đường thẳng (d1)
Trả lời (2) Xem đáp án »
 2 21824
QUẢNG CÁO

 
T
TÂM NGUYỄN
Số câu trả lời: 4
Cấp bậc:Sắt đoàn
Số điểm:20
 ĐẶT CÂU HỎI NGAY
 Thành viên hăng hái nhất
Xếp hạng tuần này
 

Xếp hạng tuần này
Xếp hạng tháng này
«¤ĎĄŘĶ¤»1215 điểm
SGP.Vịt835 điểm
ঔᴛʀầɴ✿ᴠɪếᴛ✿ᴄườɴɢ亗775 điểm
Giang Nguyễn245 điểm
Trần Viết Hoàng245 điểm
Xem thêm 
BÀI VIẾT MỚI NHẤT LỚP 9
Cảm nhận văn bản “Tôi và chúng ta” của Lưu Quang Vũ.
 2 năm trước
 3928
Phân tích văn bản “Tôi và chúng ta” của Lưu Quang Vũ.
 2 năm trước
 3442
Cảm nhận văn bản “Bắc Sơn” của Nguyễn Huy Tưởng.
 2 năm trước
 3294
Em hãy phân tích diễn biến tâm trạng và hành động của nhân vật Thơm qua hai lớp kịch trong đoạn trích hồi 4 của vở kịch “Bắc Sơn”( Nguyễn Huy Tưởng).
 2 năm trước
 4549
Phân tích văn bản “Bắc Sơn” của Nguyễn Huy Tưởng.
 2 năm trước
 3238
Xem thêm »
Gửi báo cáo thành công!
Chúng tôi
Giới thiệu công ty
Giảng viên tại Vietjack
Chính sách bảo mật
Điều khoản dịch vụ
Học tập
Khóa học, bài giảng
Câu hỏi trắc nghiệm
Câu hỏi tự luận
Bộ đề trắc nghiệm các lớp
Tài liệu tham khảo
Liên kết
Tải tài liệu miễn phí
Tài liệu giáo viên
Để học tốt
Tin tức tổng hợp
Tuyển dụng - Việc làm
Tải ứng dụng


Bài viết mới nhất
Thông tin tuyển sinh
Lớp 12
Lớp 11
Lớp 10
Lớp 9
Lớp 8
Lớp 7
Lớp 6
Lớp 5
Lớp 4
Lớp 3

© 2019 Vietjack46. All Rights Reserved 

Để giải bài toán này, ta sử dụng một số tính chất của tam giác vuông và đường cao.

1. **Tính độ dài các cạnh AB và AC:**

- Gọi \( AB = a \), \( AC = b \), và \( BC = c \) là các cạnh của tam giác vuông \( ABC \) vuông tại \( A \).
- Đường cao từ \( A \) đến \( BC \) là \( AH \), và ta biết rằng \( BH = 1 \), \( CH = 2 \).

- Theo định lý Pythagoras trong tam giác vuông \( AHB \) và \( AHC \):
\[
AB^2 = AH^2 + BH^2
\]
\[
AC^2 = AH^2 + CH^2
\]

- Từ định lý Pythagoras trong tam giác vuông \( ABC \):
\[
BC^2 = AB^2 + AC^2
\]

- Đường cao từ \( A \) chia cạnh \( BC \) thành hai đoạn \( BH \) và \( CH \), và có công thức:
\[
AH^2 = BH \cdot CH
\]
Thay \( BH = 1 \) và \( CH = 2 \):
\[
AH^2 = 1 \cdot 2 = 2
\]
\[
AH = \sqrt{2}
\]

- Thay \( AH \) vào các công thức:
\[
AB^2 = (\sqrt{2})^2 + 1^2 = 2 + 1 = 3
\]
\[
AC^2 = (\sqrt{2})^2 + 2^2 = 2 + 4 = 6
\]

- Vậy:
\[
AB = \sqrt{3}
\]
\[
AC = \sqrt{6}
\]

2. **Tính sin B và sin C:**

- Trong tam giác vuông \( ABC \):
\[
\sin B = \frac{AC}{BC}
\]
\[
\sin C = \frac{AB}{BC}
\]

- Ta có:
\[
BC^2 = AB^2 + AC^2 = 3 + 6 = 9
\]
\[
BC = \sqrt{9} = 3
\]

- Tính sin B và sin C:
\[
\sin B = \frac{AC}{BC} = \frac{\sqrt{6}}{3}
\]
\[
\sin C = \frac{AB}{BC} = \frac{\sqrt{3}}{3}
\]

Tóm lại:

- \( AB = \sqrt{3} \)
- \( AC = \sqrt{6} \)
- \( \sin B = \frac{\sqrt{6}}{3} \)
- \( \sin C = \frac{\sqrt{3}}{3} \)