Quảng cáo
2 câu trả lời 539
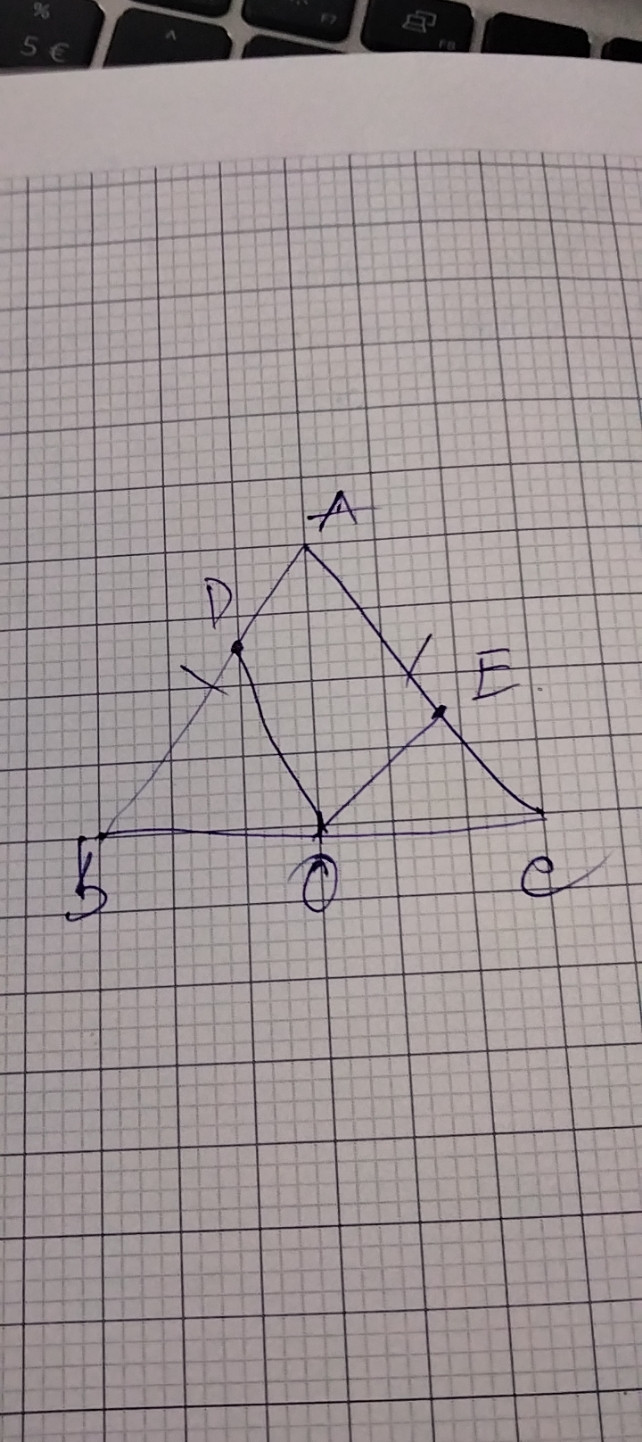
a. Do 𝐶𝐸=𝑂𝐵2𝐵𝐷⇒𝐶𝐸=𝑂𝐵.𝑂𝐶𝐵𝐷⇒𝐶𝐸𝑂𝐵=𝑂𝐶𝐵𝐷CE=BDOB2⇒CE=BDOB.OC⇒OBCE=BDOC
Lại vì tam giác ABC cân tại A nên 𝐷𝐵𝑂^=𝑂𝐶𝐸^DBO=OCE
Từ đó suy ra Δ𝐷𝐵𝑂∼Δ𝑂𝐶𝐸(𝑐−𝑔−𝑐)ΔDBO∼ΔOCE(c−g−c)
b. Do Δ𝐷𝐵𝑂∼Δ𝑂𝐶𝐸⇒𝐵𝑂𝐶𝐸=𝐷𝑂𝑂𝐸⇒𝐶𝑂𝐶𝐸=𝐷𝑂𝑂𝐸(1)ΔDBO∼ΔOCE⇒CEBO=OEDO⇒CECO=OEDO(1)
và 𝐵𝑂𝐷^=𝐶𝐸𝑂^BOD=CEO
Ta có 𝐵𝑂𝐷^+𝐷𝐸𝑂^+𝐸𝑂𝐶^=180𝑜=𝑂𝐸𝐶^+𝐷𝐸𝑂^+𝐸𝑂𝐶^BOD+DEO+EOC=180o=OEC+DEO+EOC
nên 𝐷𝑂𝐸^=𝑂𝐶𝐸^(2)DOE=OCE(2)
Từ (1), (2) suy ra Δ𝐷𝑂𝐸∼Δ𝑂𝐶𝐸(𝑐−𝑔−𝑐)⇒Δ𝐷𝑂𝐸∼Δ𝑂𝐶𝐸∼Δ𝐷𝐵𝑂.ΔDOE∼ΔOCE(c−g−c)⇒ΔDOE∼ΔOCE∼ΔDBO.
c. Từ các tam giác đồng dạng ta suy ra 𝐵𝐷𝑂^=𝐸𝐷𝑂^;𝐷𝐹𝑂^=𝐶𝐹𝑂^BDO=EDO;DFO=CFO
hay DO, EO lần lượt là các phân giác của các góc 𝐵𝐷𝐸^;𝐷𝐸𝐶^.BDE;DEC.
d. Gọi chân đường vuông góc kẻ từ O xuổng DE, AB lần lượt là H, K. Ta thấy ngay OK không đổi và OH chính là khoảng cách từ O đến ED.
Khi đó ta thấy ngay Δ𝐷𝐻𝑂=Δ𝐷𝐾𝑂ΔDHO=ΔDKO (cạnh huyền - góc nhọn)
⇒𝑂𝐻=𝑂𝐾⇒OH=OK (không đổi).
a. Do 𝐶𝐸=𝑂𝐵2𝐵𝐷⇒𝐶𝐸=𝑂𝐵.𝑂𝐶𝐵𝐷⇒𝐶𝐸𝑂𝐵=𝑂𝐶𝐵𝐷CE=BDOB2⇒CE=BDOB.OC⇒OBCE=BDOC
Lại vì tam giác ABC cân tại A nên 𝐷𝐵𝑂^=𝑂𝐶𝐸^DBO=OCE
Từ đó suy ra Δ𝐷𝐵𝑂∼Δ𝑂𝐶𝐸(𝑐−𝑔−𝑐)ΔDBO∼ΔOCE(c−g−c)
b. Do Δ𝐷𝐵𝑂∼Δ𝑂𝐶𝐸⇒𝐵𝑂𝐶𝐸=𝐷𝑂𝑂𝐸⇒𝐶𝑂𝐶𝐸=𝐷𝑂𝑂𝐸(1)ΔDBO∼ΔOCE⇒CEBO=OEDO⇒CECO=OEDO(1)
và 𝐵𝑂𝐷^=𝐶𝐸𝑂^BOD=CEO
Ta có 𝐵𝑂𝐷^+𝐷𝐸𝑂^+𝐸𝑂𝐶^=180𝑜=𝑂𝐸𝐶^+𝐷𝐸𝑂^+𝐸𝑂𝐶^BOD+DEO+EOC=180o=OEC+DEO+EOC
nên 𝐷𝑂𝐸^=𝑂𝐶𝐸^(2)DOE=OCE(2)
Từ (1), (2) suy ra Δ𝐷𝑂𝐸∼Δ𝑂𝐶𝐸(𝑐−𝑔−𝑐)⇒Δ𝐷𝑂𝐸∼Δ𝑂𝐶𝐸∼Δ𝐷𝐵𝑂.ΔDOE∼ΔOCE(c−g−c)⇒ΔDOE∼ΔOCE∼ΔDBO.
c. Từ các tam giác đồng dạng ta suy ra 𝐵𝐷𝑂^=𝐸𝐷𝑂^;𝐷𝐹𝑂^=𝐶𝐹𝑂^BDO=EDO;DFO=CFO
hay DO, EO lần lượt là các phân giác của các góc 𝐵𝐷𝐸^;𝐷𝐸𝐶^.BDE;DEC.
d. Gọi chân đường vuông góc kẻ từ O xuổng DE, AB lần lượt là H, K. Ta thấy ngay OK không đổi và OH chính là khoảng cách từ O đến ED.
Khi đó ta thấy ngay Δ𝐷𝐻𝑂=Δ𝐷𝐾𝑂ΔDHO=ΔDKO (cạnh huyền - góc nhọn)
⇒𝑂𝐻=𝑂𝐾⇒OH=OK (không đổi).
Quảng cáo
Câu hỏi hot cùng chủ đề
-
102494
-
Hỏi từ APP VIETJACK67797
-
55981
-
46625
-
42380
-
32714


![CEO tập đoàn Lục thị[nk]](/upload/images/user/1757779274-anh-chup-man-hinh-2025-09-09-000613png.png)









