Giải giúp mình với:
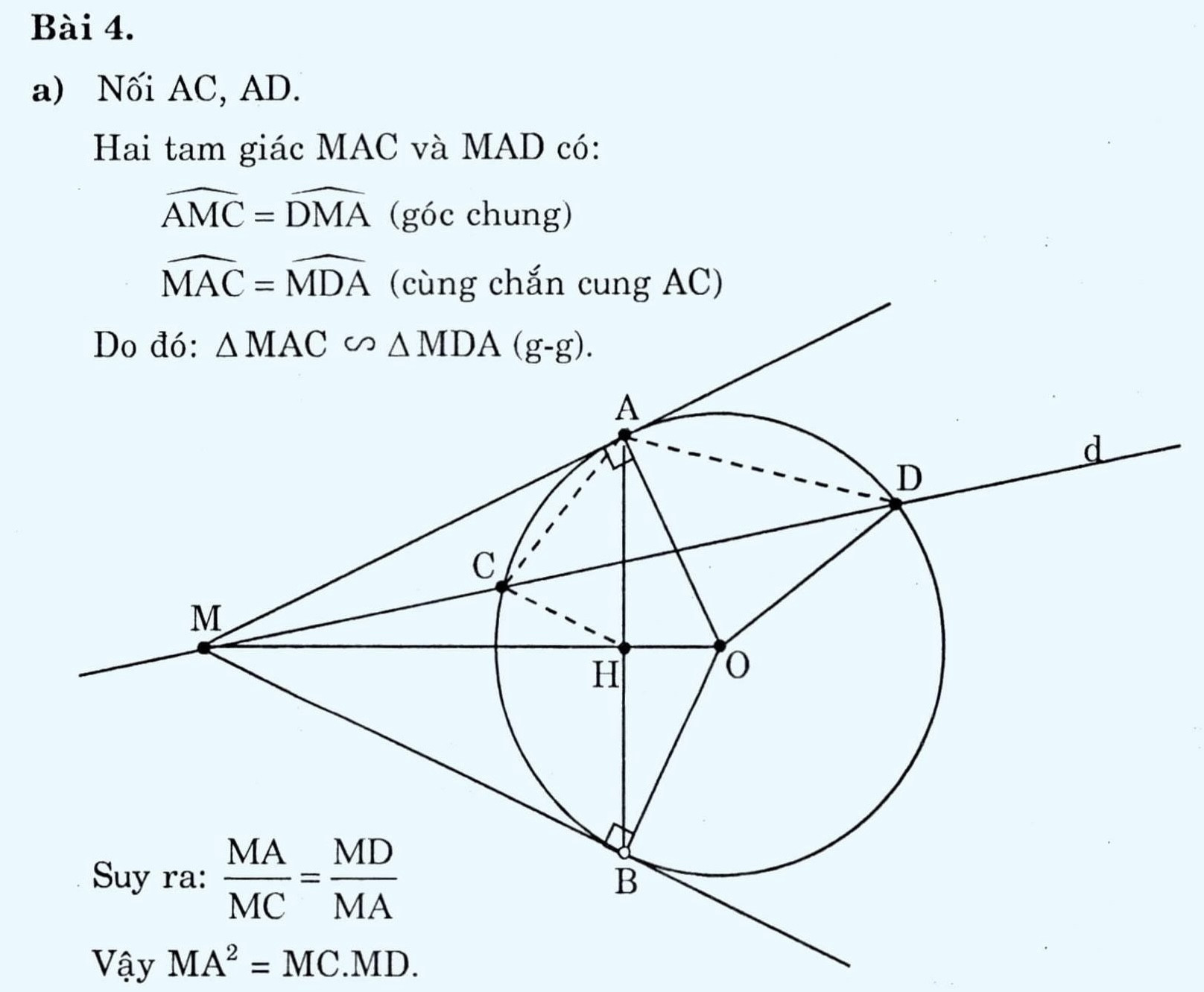
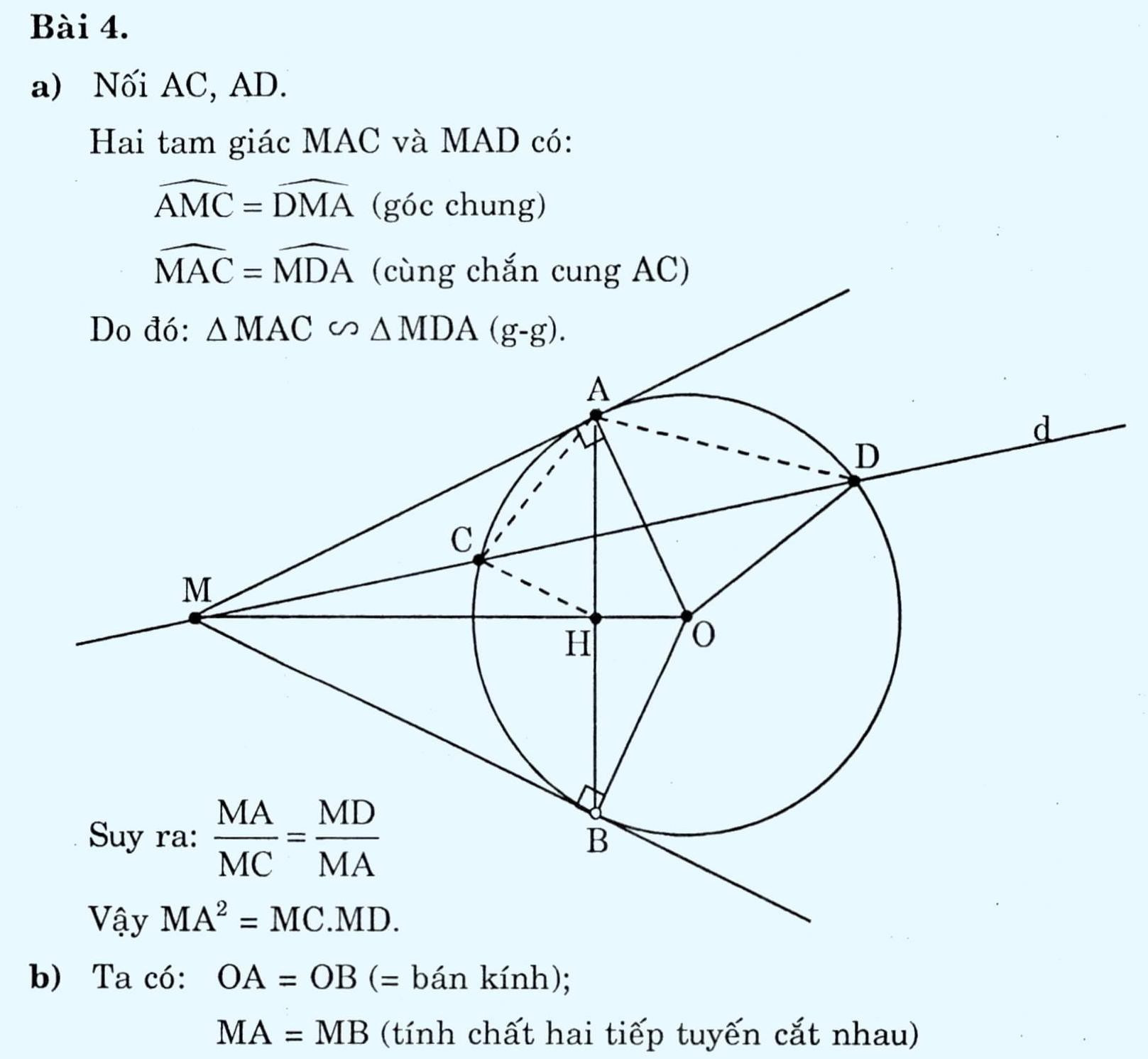
Cho đường tròn (O) và một điểm M nằm ngoài (O) kẻ hai tiếp tuyến MA; MB và cát tuyến MCD (không qua O)
a) Chứng minh MA² = MC.MD
b) Gọi H là giao điểm của AB và OM. Chứng minh CHOD nội tiếp
c) cho MC.MD=144; OM =13cm. Tính độ dài (O) và diện tích hình tròn (O)
Cho đường tròn (O) và một điểm M nằm ngoài (O) kẻ hai tiếp tuyến MA; MB và cát tuyến MCD (không qua O)
a) Chứng minh MA² = MC.MD
b) Gọi H là giao điểm của AB và OM. Chứng minh CHOD nội tiếp
c) cho MC.MD=144; OM =13cm. Tính độ dài (O) và diện tích hình tròn (O)
Quảng cáo
3 câu trả lời 529
Để giải bài toán này, ta sẽ sử dụng một số định lý trong hình học đường tròn.
Định lý 1: Đường tiếp tuyến tại một điểm trên đường tròn là vuông góc với đường phân giác của góc tạo bởi đường tiếp tuyến và đoạn thẳng nối từ điểm tiếp tuyến đến tâm của đường tròn.
Định lý 2: Hai tiếp tuyến từ một điểm bên ngoài đường tròn bằng nhau. Với bài toán trên, ta có:
- Hai tiếp tuyến MA và MB từ điểm M đến đường tròn (O)
- Đường chéo CD của tứ giác AMCD. Do đó, ta có thể áp dụng định lý 2 để suy ra rằng MA = MB.
Tiếp theo, ta sẽ sử dụng định lý 1 để chứng minh rằng đường chéo CD của tứ giác AMCD là đường phân giác của góc AMD.
Vậy, ta đã chứng minh được rằng đường chéo CD của tứ giác AMCD là đường phân giác của góc AMD.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490
Gửi báo cáo thành công!