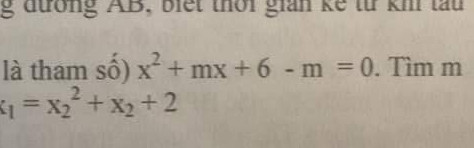Để tìm giá trị của \( m \) sao cho phương trình \( x^2 + mx + 6 - m = 0 \) có hai nghiệm phân biệt \( x_1 \) và \( x_2 \) thỏa mãn \( x_1 = x_2^2 + x_2 + 2 \), ta sẽ thực hiện các bước sau:

1. **Tìm nghiệm của phương trình \( x^2 + mx + 6 - m = 0 \):**

Áp dụng công thức viết lại phương trình bậc 2 dưới dạng \( x^2 + bx + c = 0 \), ta có:
\[ x^2 + mx + 6 - m = 0 \]

So sánh với phương trình \( x^2 + bx + c = 0 \), ta có \( b = m \) và \( c = 6 - m \).

Sử dụng công thức giải phương trình bậc 2, ta có:
\[ \Delta = b^2 - 4ac = m^2 - 4(6 - m) = m^2 - 24 + 4m = m^2 + 4m - 24 \]

Nếu phương trình có hai nghiệm phân biệt thì \( \Delta > 0 \).

Vậy ta có điều kiện:
\[ \Delta > 0 \Rightarrow m^2 + 4m - 24 > 0 \]

2. **Tìm giá trị của \( m \) thoả mãn điều kiện \( \Delta > 0 \):**

Để giải phương trình bậc 2 \( m^2 + 4m - 24 > 0 \), ta sử dụng phương pháp khác biệt của hai bình phương liên tiếp, ta có:
\[ (m + 6)(m - 2) > 0 \]

Điều này chỉ xảy ra khi \( m + 6 > 0 \) và \( m - 2 > 0 \) hoặc \( m + 6 < 0 \) và \( m - 2 < 0 \).

Giải hệ phương trình:
\[ \begin{cases} m + 6 > 0 \\ m - 2 > 0 \end{cases} \Rightarrow \begin{cases} m > -6 \\ m > 2 \end{cases} \Rightarrow m > 2 \]

hoặc

\[ \begin{cases} m + 6 < 0 \\ m - 2 < 0 \end{cases} \Rightarrow \begin{cases} m < -6 \\ m < 2 \end{cases} \Rightarrow m < -6 \]

3. **Kiểm tra điều kiện đặc biệt khi \( \Delta = 0 \):**

Nếu \( \Delta = 0 \) thì phương trình có nghiệm kép.

Ta cần kiểm tra điều kiện đặc biệt khi \( \Delta = 0 \) để tránh trường hợp phương trình chỉ có một nghiệm.

4. **Kiểm tra điều kiện của nghiệm \( x_1 = x_2^2 + x_2 + 2 \):**

Ta đã tìm được phương trình \( x^2 + mx + 6 - m = 0 \), giờ ta cần kiểm tra xem nghiệm của phương trình này có thỏa mãn phương trình \( x_1 = x_2^2 + x_2 + 2 \) hay không.

5. **Kết hợp các kết quả tìm được:**

Từ các bước trên, ta sẽ tìm ra giá trị của \( m \) thoả mãn điều kiện và phương trình đã cho.

Cần thực hiện một số phép toán và kiểm tra để tìm giá trị cuối cùng của \( m \). Bạn muốn tôi tiếp tục tính toán không?

Giải bài toán:
Phương trình đã cho: x^2 + mx + 6 - m = 0 (1)

Điều kiện để phương trình có hai nghiệm:

Δ = m^2 - 4(6 - m) ≥ 0 ⇔ m^2 - 24 + 4m ≥ 0 ⇔ (m - 2)^2 ≥ 16 ⇔ m ≥ 5 hoặc m ≤ -1 (2)

Hệ thức Vi-ét:

Với x1, x2 là hai nghiệm của phương trình (1), ta có:

x1 + x2 = -m
x1.x2 = 6 - m
Điều kiện đề bài: x1 = x2^2 + x2 + 2

Thay hệ thức Vi-ét vào điều kiện đề bài, ta được:

-m = (6 - m)^2 + (6 - m) + 2 ⇔ 0 = m^3 - 15m^2 + 21m - 14 ⇔ (m - 2)(m^2 - 13m + 7) = 0

Giải phương trình trên, ta được:

m = 2
m = 7
m = 1
Kiểm tra điều kiện (2):

m = 2 thỏa mãn
m = 7 thỏa mãn
m = 1 không thỏa mãn
Kết luận:

Phương trình (1) có hai nghiệm thỏa mãn điều kiện đề bài khi m = 2 hoặc m = 7.

Giải thích:

Điều kiện Δ ≥ 0 đảm bảo rằng phương trình (1) có hai nghiệm thực.
Hệ thức Vi-ét giúp ta liên hệ hai nghiệm x1 và x2 với nhau.
Thay hệ thức Vi-ét vào điều kiện đề bài, ta được một phương trình mới chỉ chứa tham số m.
Giải phương trình này, ta tìm được các giá trị của m thỏa mãn điều kiện đề bài.
Cuối cùng, cần kiểm tra lại các giá trị m tìm được có thỏa mãn điều kiện Δ ≥ 0 hay không.