Cho tam giác ABC có AB < AC, AD là tia phân giác của góc BAD

Lời giải Bài 15 trang 71 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

150
« Trang trước
Chia sẻ
Trang sau »
Giải SBT Toán 7 Cánh diều Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Bài 15 trang 71 SBT Toán 7 Tập 2: Cho tam giác ABC có AB < AC, AD là tia phân giác của BAD^ (D ∈ BC). Chứng minh ADB^<ADC^.

Lời giải

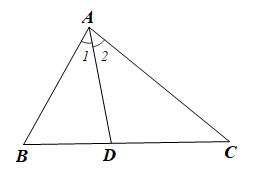
Sách bài tập Toán 7 Bài 2 (Cánh diều): Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác  (ảnh 1) 

Xét tam giác ABC có AB < AC (giả thiết)

Suy ra C^<B^ (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn).

Vì AD là tia phân giác của góc BAC nên A^1=A^2.

Xét ∆ABD có: A^1+B^+ADB^=180° (tổng ba góc của một tam giác).

Suy ra ADB^=180°−A^1−B^ (1)

Xét ∆ACD có: A^2+C^+ADC^=180° (tổng ba góc của một tam giác).

Suy ra ADC^=180°−A^2−C^ (2)

Mà A^1=A^2 (chứng minh trên) và B^>C^ (chứng minh trên) (3)

Từ (1), (2) và (3) ta có ADB^<ADC^

Vậy ADB^<ADC^.

Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:

Bài 12 trang 70 SBT Toán 7 Tập 2: Cho tam giác ABC có A^=3B^=6C^. a) Tìm số đo góc lớn nhất, góc bé nhất của tam giác ABC...

Bài 13 trang 70 SBT Toán 7 Tập 2: Cho tam giác ABC có góc A tù. Trên cạnh AC lấy điểm D và E (D nằm giữa A và E). Chứng minh BA < BD < BE < BC...

Bài 14 trang 70, 71 SBT Toán 7 Tập 2: a) Cho tam giác ABC có AB = 15 cm, BC = 8 cm. Tính độ dài cạnh AC, biết độ dài của nó (theo đơn vị xăng-ti-mét) là một số nguyên tố lớn hơn bình phương của 4...

Bài 15 trang 71 SBT Toán 7 Tập 2: Cho tam giác ABC có AB < AC, AD là tia phân giác của BAD^ (D ∈ BC). Chứng minh ADB^<ADC^...

Bài 16 trang 71 SBT Toán 7 Tập 2: Cho tam giác ABC có A^=110° và B^=C^. Trên cạnh BC lấy điểm D sao cho ADC^=105°. Từ C kẻ đường thẳng song song với AD cắt tia BA tại E. Chứng minh...

Bài 17 trang 71 SBT Toán 7 Tập 2: Cho tam giác ABC, điểm D nằm giữa hai điểm B và C. Chứng minh AD nhỏ hơn nửa chu vi của tam giác ABC...

Bài 18* trang 71 SBT Toán 7 Tập 2: Chứng minh rằng trong một tam giác, độ dài cạnh lớn nhất sẽ lớn hơn hoặc bằng 13 chu vi của tam giác nhưng nhỏ hơn nửa chu vi của tam giác đó...

Bài viết liên quan

150
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm

    Bài viết có lượt xem cao