Cho tam giác ABC có trọng tâm g gọi a'b'c' lần lượt là trung điểm của agbgcg chứ

huhu59076@gmail.com Hỏi từ APP VIETJACK

· 05:28 02/04/2025

Cho tam giác ABC có trọng tâm g gọi a'b'c' lần lượt là trung điểm của agbgcg chứng minh tam giác a'b' đồng dạng với tam giác ABC

Lưu câu hỏi Lưu

Hỏi chi tiết

Quảng cáo

9 tháng trước

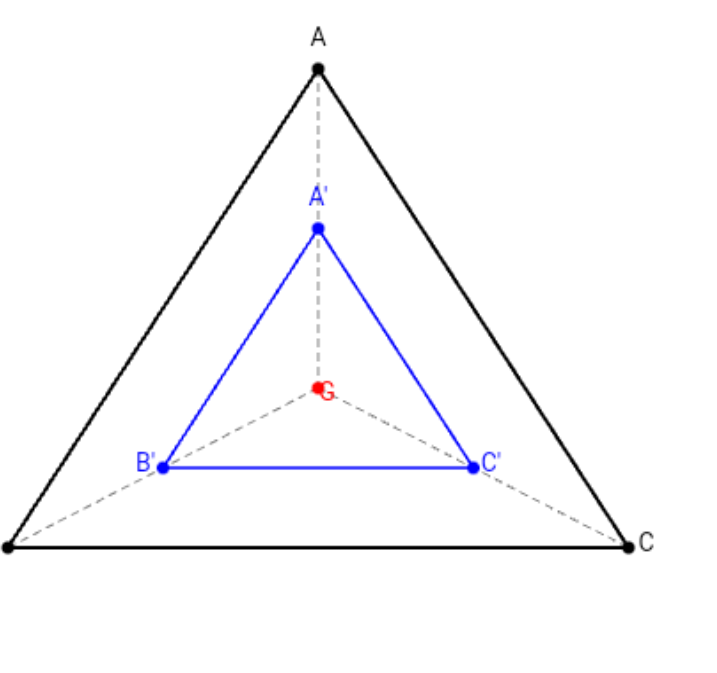
Xét $\triangle ABG$:

$A'$ là trung điểm $AG$ (giả thiết)

$B'$ là trung điểm $BG$ (giả thiết)

$\implies A'B'$ là đường trung bình của $\triangle ABG$.

$\implies A'B' = \frac{1}{2} AB$ (Tính chất đường trung bình) (1)

Xét $\triangle BCG$:

$B'$ là trung điểm $BG$ (giả thiết)

$C'$ là trung điểm $CG$ (giả thiết)

$\implies B'C'$ là đường trung bình của $\triangle BCG$.

$\implies B'C' = \frac{1}{2} BC$ (Tính chất đường trung bình) (2)

Xét $\triangle CAG$:

$C'$ là trung điểm $CG$ (giả thiết)

$A'$ là trung điểm $AG$ (giả thiết)

$\implies C'A'$ là đường trung bình của $\triangle CAG$.

$\implies C'A' = \frac{1}{2} CA$ (Tính chất đường trung bình) (3)

Từ (1), (2) và (3) suy ra:

$\frac{A'B'}{AB} = \frac{B'C'}{BC} = \frac{C'A'}{CA} = \frac{1}{2}$

Xét $\triangle A'B'C'$ và $\triangle ABC$ có:

$\frac{A'B'}{AB} = \frac{B'C'}{BC} = \frac{C'A'}{CA}$

Vậy $\triangle A'B'C' \sim \triangle ABC$ (trường hợp cạnh - cạnh - cạnh).

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

Quảng cáo

Bạn hỏi - Chuyên gia trả lời

Bạn cần hỏi gì?