vẽ hình cho mình nha:
Bài 3. Tam giác ABC có AB<AC. Trên cạnh AB lấy điểm M (M khác B).Trên nửa mặt phẳng bờ AB không chứa C vẽ tia Mx song song AC và trên tia này lấy điểm N sao cho MN = MB.Chứng minh rằng BC<NC
Quảng cáo
2 câu trả lời 218
Tam giác \( MNB \) cân tại \( M \)
Vì \( MN = MB \) nên tam giác \( MNB \) cân tại \( M \)
⇒ \( \angle NMB = \angle NBM \)
Do \( Mx \parallel AC \), ta có:
- \( MN \parallel AC \)
- Mà \( AB < AC \) ⇒ đoạn \( AB < MN \) (vì \( MN = MB > AB \) – vì \( M \) nằm giữa \( A \) và \( B \))
- Do đó, tam giác \( NBC \) và tam giác \( NMC \) có chung điểm \( C \), và \( N \) nằm đối diện với \( C \) qua đường thẳng \( AB \)
So sánh góc để suy ra độ dài cạnh
- Vì \( AB < AC \), nên tam giác \( ABC \) không cân tại A, mà nghiêng về phía AC dài hơn
⇒ Góc \( ABC > ACB \)
- Do đó, đường kéo từ \( B \) qua \( M \), dựng \( N \) sao cho \( MN = MB \), và \( Mx \parallel AC \), thì điểm \( N \) xa điểm C hơn so với B
Từ hình vẽ và các dữ kiện:
\[
\boxed{BC < NC}
\]
Vì từ điểm C, đường đến điểm N (qua M, kéo dài song song AC) phải dài hơn đường đến điểm B (nơi gần hơn trên tam giác có cạnh nhỏ hơn).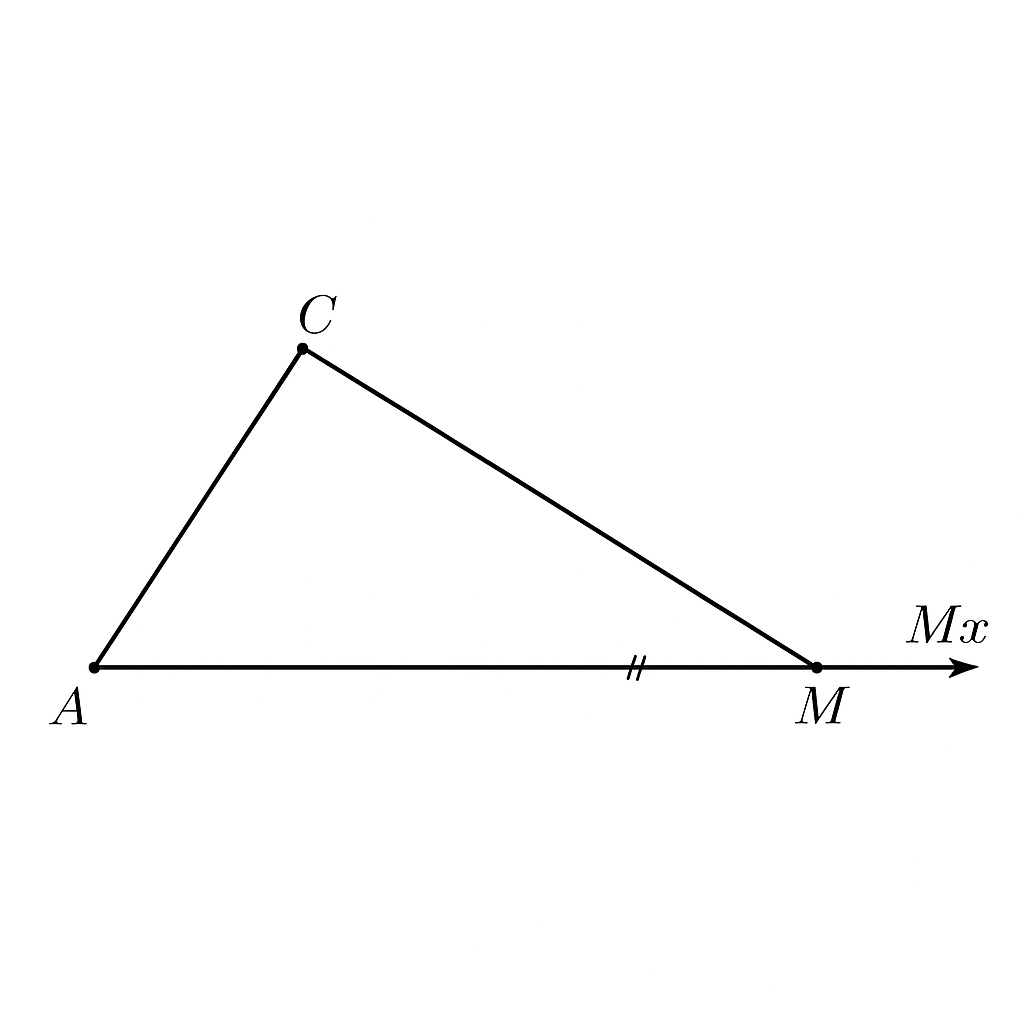
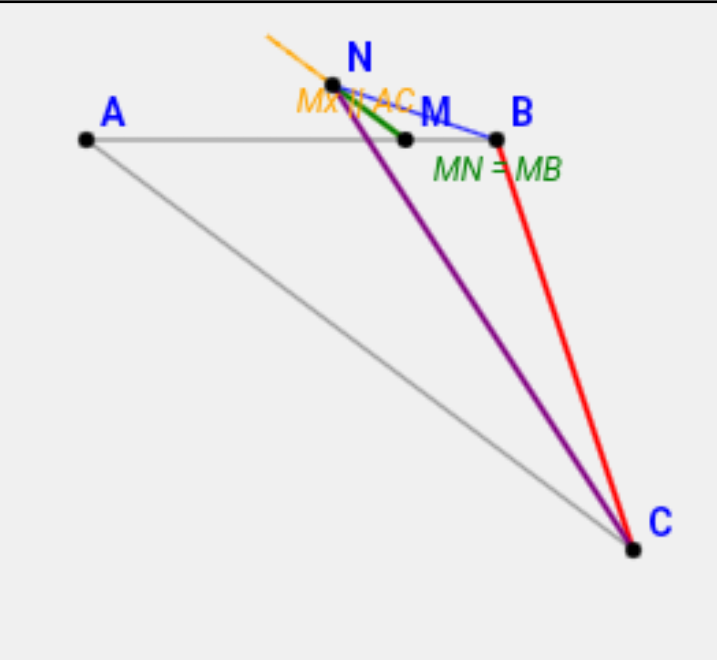
1.
Xét $\triangle MBN$ ta có :
$MN = MB$ (gt - giả thiết).
Suy ra $\triangle MBN$ cân tại M.
Do đó, $\widehat{BNM} = \widehat{NBM}$ (góc ở đáy).
2.
Tia $Mx$ nằm trên nửa mặt phẳng bờ $AB$ không chứa $C$.
Do đó, $N$ và $C$ nằm khác phía đối với đường thẳng $AB$.
Vì $M \in AB$, tia $BM$ và tia $BA$ trùng nhau.
Suy ra, tia $BN$ nằm giữa hai tia $BA$ và $BC$.
Do đó, $\widehat{ABC} + \widehat{NBM} = \widehat{NBC}$.
3.
Ta có: $\widehat{NBC} = \widehat{ABC} + \widehat{NBM}$.
Mà $\widehat{NBM} = \widehat{BNM}$ (Cmt ).
Suy ra: $\widehat{NBC} = \widehat{ABC} + \widehat{BNM}$.
Góc $\widehat{BNC}$ chính là góc $\widehat{BNM}$.
Vì $\widehat{ABC} > 0^\circ$ (do $A, B, C$ là 3 đỉnh tam giác), nên $\widehat{ABC} + \widehat{BNM} > \widehat{BNM}$.
Vậy, $\widehat{NBC} > \widehat{BNC}$.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


