Giải bất phương trình
X+√2x-1/√x+2≤0
Quảng cáo
3 câu trả lời 921
$X + \frac{\sqrt{2x - 1}}{\sqrt{x} + 2} \le 0$
$X(\sqrt{x} + 2) + \sqrt{2x - 1} \le 0$
$X(\sqrt{x} + 2)^2 + \sqrt{2x - 1}(\sqrt{x} + 2) \le 0$
$(x + 1)(\sqrt{x} + 2)(\sqrt{2x - 1}) \le 0$
TH1: $x + 1 \le 0$:
Bất phương trình luôn đúng với mọi $x \le -1$.
TH2: $\sqrt{x} + 2 \le 0$:
Vô nghiệm vì $\sqrt{x} \ge 0$ với mọi $x \ge 0$.
TH3: $\sqrt{2x - 1} \le 0$:
Bất phương trình chỉ đúng khi $x \le \frac{1}{2}$.
Tập nghiệm của bất phương trình là:
$S = \{ x | x \le -1 \text{ hoặc } x \le \frac{1}{2} \}$
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
89948
Đã trả lời bởi chuyên gia
89948 -
 Đã trả lời bởi chuyên gia
60184
Đã trả lời bởi chuyên gia
60184 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
59502
Đã trả lời bởi chuyên gia
59502 -
 Đã trả lời bởi chuyên gia
51140
Đã trả lời bởi chuyên gia
51140 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
48636
Đã trả lời bởi chuyên gia
48636 -
 Đã trả lời bởi chuyên gia
38917
Đã trả lời bởi chuyên gia
38917
Gửi báo cáo thành công!

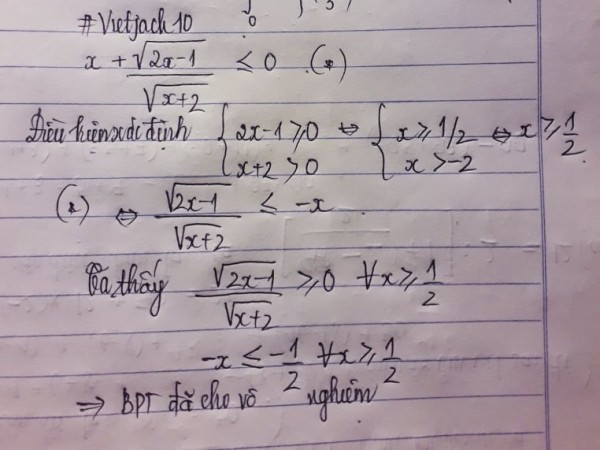
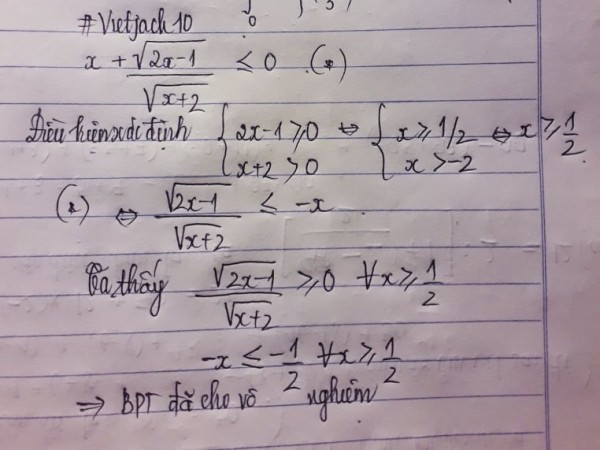 M
M
