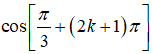Cho .Khẳng định nào sau đây đúng?
A. sin(α – π) ≥ 0.
B.sin(α – π) ≤ 0.
C. sin(α – π) > 0.
D. sin(α – π) < 0.
Phương Linh
· 2 năm trước
cho 0<a<pi. khẳng định nào đúng
Phương Linh
· 2 năm trước
a. sin>0 b. cos >0. c. tan>0. d.cot<0
Quảng cáo
10 câu trả lời 60132
Giải bài toán: Xét dấu của sin()
Phân tích bài toán
Cho ![]() . Ta cần xác định dấu của biểu thức sin().
. Ta cần xác định dấu của biểu thức sin().
Biến đổi biểu thức sin()
Sử dụng công thức lượng giác:
![]()
Thay a và b = , ta có:
![]()
Dùng giá trị lượng giác đặc biệt của :
![]()
Thay vào, ta được:
![]()
Xét dấu của sin()
Vì ![]() , nên:
, nên:
![]()
Do đó:
![]()
Kết luận
Khẳng định đúng là:
![]()
Phac Phac
· 2 năm trước
Cho e hỏi s biết được alpha trừ pi thuộc góc p tư thứ 3 ạ
$0<\alpha < \dfrac{\pi}{2}$
$\to 0-\pi < \alpha - \pi < \dfrac{\pi}{2} - \pi$
$\to -\pi < \alpha - \pi < -\dfrac{\pi}{2} < 0$
Đáp án $D$
Ta có
Do đó; điểm cuối cung α – π thuộc góc phần tư thứ 3 nên sin(α – π) < 0.
CEO Tập Đoàn Học Bá ><ヾ(•ω•`)o
· 1 năm trước
evowar
♈ㅤूाीू ¯\(▀̿Ĺ̯▀̿ ̿)/¯
· 1 năm trước
evowar.io
Thông tin hữu ích
Công thức lượng giác: sin(x−π)=−sin(x)sine open paren x minus pi close paren equals negative sine open paren x close paren
sin(𝑥−𝜋)=−sin(𝑥)
.
Dấu của hàm sinsine
sin
trong các góc phần tư.
Cách giải
Sử dụng công thức lượng giác để biến đổi biểu thức và xác định dấu của nó.
Bước 1 . Biến đổi biểu thức sin(α−π)sine open paren alpha minus pi close paren
sin(𝛼−𝜋)
:
Áp dụng công thức sin(x−π)=−sin(x)sine open paren x minus pi close paren equals negative sine open paren x close paren
sin(𝑥−𝜋)=−sin(𝑥)
.
Ta có sin(α−π)=−sin(α)sine open paren alpha minus pi close paren equals negative sine open paren alpha close paren
sin(𝛼−𝜋)=−sin(𝛼)
.
Bước 2 . Xác định dấu của sin(α)sine open paren alpha close paren
sin(𝛼)
:
Vì 0<α<π20 is less than alpha is less than the fraction with numerator pi and denominator 2 end-fraction
0<𝛼<𝜋2
, αalpha
𝛼
nằm trong góc phần tư thứ nhất.
Trong góc phần tư thứ nhất, giá trị của sin(α)sine open paren alpha close paren
sin(𝛼)
luôn dương, tức là sin(α)>0sine open paren alpha close paren is greater than 0
sin(𝛼)>0
.
Bước 3 . Xác định dấu của −sin(α)negative sine open paren alpha close paren
−sin(𝛼)
:
Vì sin(α)>0sine open paren alpha close paren is greater than 0
sin(𝛼)>0
, khi nhân với -1negative 1
−1
, ta được −sin(α)<0negative sine open paren alpha close paren is less than 0
−sin(𝛼)<0
.
Do đó, sin(α−π)<0sine open paren alpha minus pi close paren is less than 0
sin(𝛼−𝜋)<0
.
Lời giải
Khẳng định đúng là sin(α−π)<0sine open paren alpha minus pi close paren is less than 0
sin(𝛼−𝜋)<0
.
Công thức lượng giác: sin(x−π)=−sin(x)sine open paren x minus pi close paren equals negative sine open paren x close paren
sin(𝑥−𝜋)=−sin(𝑥)
.
Dấu của hàm sinsine
sin
trong các góc phần tư.
Cách giải
Sử dụng công thức lượng giác để biến đổi biểu thức và xác định dấu của nó.
Bước 1 . Biến đổi biểu thức sin(α−π)sine open paren alpha minus pi close paren
sin(𝛼−𝜋)
:
Áp dụng công thức sin(x−π)=−sin(x)sine open paren x minus pi close paren equals negative sine open paren x close paren
sin(𝑥−𝜋)=−sin(𝑥)
.
Ta có sin(α−π)=−sin(α)sine open paren alpha minus pi close paren equals negative sine open paren alpha close paren
sin(𝛼−𝜋)=−sin(𝛼)
.
Bước 2 . Xác định dấu của sin(α)sine open paren alpha close paren
sin(𝛼)
:
Vì 0<α<π20 is less than alpha is less than the fraction with numerator pi and denominator 2 end-fraction
0<𝛼<𝜋2
, αalpha
𝛼
nằm trong góc phần tư thứ nhất.
Trong góc phần tư thứ nhất, giá trị của sin(α)sine open paren alpha close paren
sin(𝛼)
luôn dương, tức là sin(α)>0sine open paren alpha close paren is greater than 0
sin(𝛼)>0
.
Bước 3 . Xác định dấu của −sin(α)negative sine open paren alpha close paren
−sin(𝛼)
:
Vì sin(α)>0sine open paren alpha close paren is greater than 0
sin(𝛼)>0
, khi nhân với -1negative 1
−1
, ta được −sin(α)<0negative sine open paren alpha close paren is less than 0
−sin(𝛼)<0
.
Do đó, sin(α−π)<0sine open paren alpha minus pi close paren is less than 0
sin(𝛼−𝜋)<0
.
Lời giải
Khẳng định đúng là sin(α−π)<0sine open paren alpha minus pi close paren is less than 0
sin(𝛼−𝜋)<0
.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
14947
Đã trả lời bởi chuyên gia
14947 -
 Đã trả lời bởi chuyên gia
12761
Đã trả lời bởi chuyên gia
12761 -
 Đã trả lời bởi chuyên gia
11784
Đã trả lời bởi chuyên gia
11784 -
 Đã trả lời bởi chuyên gia
11159
Đã trả lời bởi chuyên gia
11159 -
 Đã trả lời bởi chuyên gia
9916
Đã trả lời bởi chuyên gia
9916 -
 Đã trả lời bởi chuyên gia
9893
Đã trả lời bởi chuyên gia
9893
Gửi báo cáo thành công!

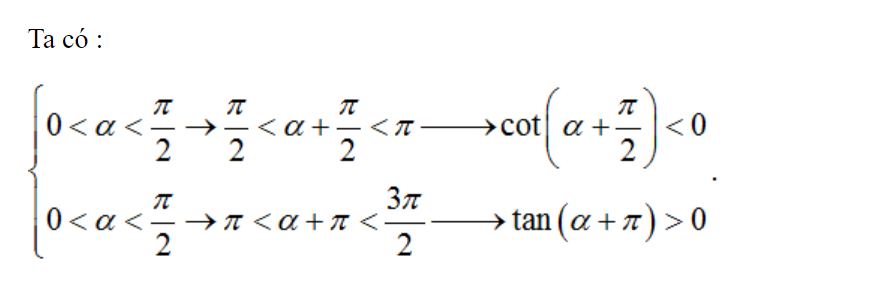
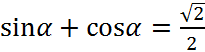
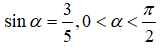
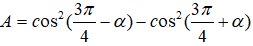
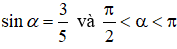
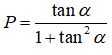 là :
là :