Chúng ta sẽ giải bài hình học này theo từng phần, sử dụng các định lý quen thuộc như định lý tiếp tuyến, tam giác đồng dạng, và hệ thức hình học trong đường tròn.

Giả thiết tổng quát:
• (O) là đường tròn tâm O, bán kính R = \frac{AD}{2}
• S nằm ngoài đường tròn (O), SA là tiếp tuyến tại A
• Qua A, kẻ đường thẳng vuông góc với OS, cắt (O) tại điểm thứ hai là B
• SD cắt (O) tại điểm thứ hai là C

a) Chứng minh: SA^2 = SH \cdot SO và SB là tiếp tuyến của (O)
Chứng minh SA^2 = SH \cdot SO:
• Tam giác SAO vuông tại A (do SA là tiếp tuyến, OA \perp SA)
• AH \perp OS tại H nên AH là đường cao từ A trong tam giác SAO
• Áp dụng hệ thức lượng trong tam giác vuông:
SA^2 = SH \cdot SO
Chứng minh SB là tiếp tuyến của (O):
• AB là đường thẳng cắt (O) tại A và B, với AB \perp OS
• SA là tiếp tuyến tại A, nên \angle SAB = \angle OAB = 90^\circ
• Do đó, tam giác SAB vuông tại A, và SB \perp OB
• Mà OB là bán kính, nên SB vuông góc với bán kính tại tiếp điểm ⇒ SB là tiếp tuyến của (O) tại B

b) Chứng minh 4 điểm O, S, A, B cùng thuộc một đường tròn
Ta chứng minh tứ giác OSAB nội tiếp:
• Từ phần a, ta có \angle SAO = 90^\circ và \angle SBO = 90^\circ
• Hai góc đối của tứ giác cùng bằng 90^\circ ⇒ tổng bằng 180^\circ
• ⇒ Tứ giác OSAB nội tiếp

c) SD cắt (O) tại C. Chứng minh: SC \cdot SD = SH \cdot SO
• Từ phần a, ta đã có SA^2 = SH \cdot SO
• Mà SA là tiếp tuyến từ S đến (O), nên theo định lý về tiếp tuyến và cát tuyến:
SC \cdot SD = SA^2
• Kết hợp lại:
SC \cdot SD = SA^2 = SH \cdot SO
• ⇒ Điều phải chứng minh

Nếu bạn muốn mình vẽ hình minh họa hoặc giải thích thêm về định lý nào trong bài, mình sẵn sàng hỗ trợ!

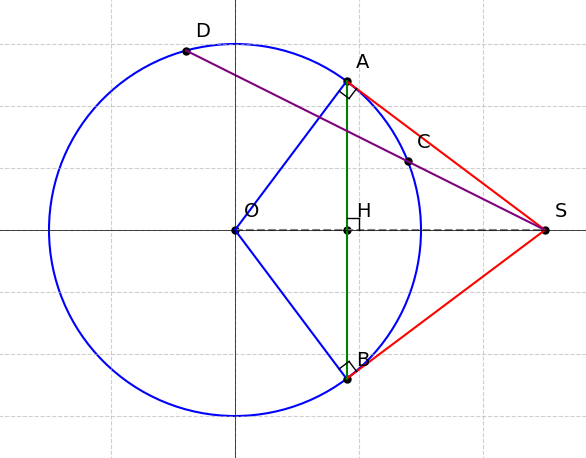a) 

 Xét $\displaystyle \triangle SAO$ vuông tại A, đường cao AH:
$\displaystyle \implies SA^2 = SH \cdot SO$ (Hệ thức lượng)

 Xét $\displaystyle \triangle SAO$ và $\displaystyle \triangle SBO$:
- $\displaystyle SO$ chung
- $\displaystyle OA = OB = R$
- $\displaystyle SA = SB$ (Tính chất hai tiếp tuyến cắt nhau, hoặc chứng minh $\displaystyle \triangle SAO = \triangle SBO$ như trên)
$\displaystyle \implies \triangle SAO = \triangle SBO$ (c.c.c)
$\displaystyle \implies \widehat{SBO} = \widehat{SAO} = 90^\circ$
$\displaystyle \implies SB \perp OB$
$\displaystyle \implies$ SB là tiếp tuyến của (O).

b) 

 Xét tứ giác OASB:
$\displaystyle \widehat{SAO} = 90^\circ$ (SA là tiếp tuyến)
$\displaystyle \widehat{SBO} = 90^\circ$ (SB là tiếp tuyến)
$\displaystyle \implies \widehat{SAO} + \widehat{SBO} = 180^\circ$
$\displaystyle \implies$ Tứ giác OASB nội tiếp đường tròn đường kính SO.

c) 

 Xét $\displaystyle \triangle SAC$ và $\displaystyle \triangle SDA$:
- $\displaystyle \widehat{S}$ chung
- $\displaystyle \widehat{SAC} = \widehat{SDA}$ (cùng chắn cung AC)
$\displaystyle \implies \triangle SAC \sim \triangle SDA$ (g.g)
$\displaystyle \implies \frac{SA}{SD} = \frac{SC}{SA} \implies SA^2 = SC \cdot SD$

 Từ (a) ta có: $\displaystyle SA^2 = SH \cdot SO$
 $\displaystyle \implies SC \cdot SD = SH \cdot SO$ (đpcm).