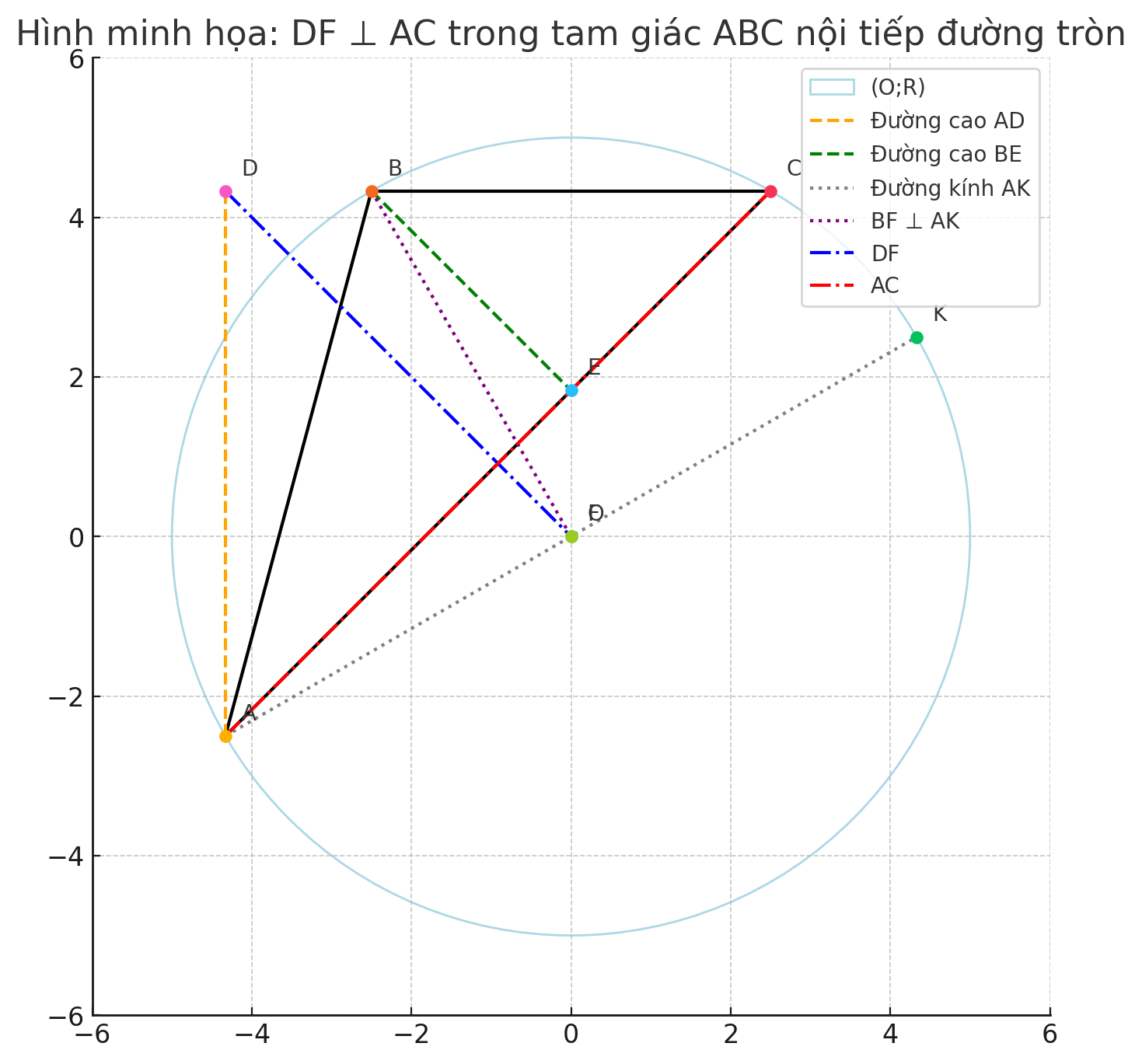
1. Tóm tắt giả thiết và ký hiệu:
(O; R) là đường tròn.

BC là dây cung không đi qua tâm O.

A là một điểm trên cung lớn BC sao cho tam giác ABC có 3 góc nhọn và AB < AC.

𝐴
𝐷
AD,
𝐵
𝐸
BE là các đường cao của tam giác
𝐴
𝐵
𝐶
ABC.

AK là đường kính của đường tròn.

F là hình chiếu vuông góc của điểm B trên đường thẳng AK.

Cần chứng minh:
𝐷
𝐹
⊥
𝐴
𝐶
DF⊥AC

2. Phân tích hình học:
Vì
𝐴
𝐷
AD và
𝐵
𝐸
BE là đường cao nên:

𝐷
∈
𝐵
𝐶
D∈BC,
𝐴
𝐷
⊥
𝐵
𝐶
AD⊥BC

𝐸
∈
𝐴
𝐶
E∈AC,
𝐵
𝐸
⊥
𝐴
𝐶
BE⊥AC

Hạ
𝐵
𝐹
⊥
𝐴
𝐾
BF⊥AK, điểm F thuộc AK.

3. Ý tưởng chính của chứng minh:
Để chứng minh
𝐷
𝐹
⊥
𝐴
𝐶
DF⊥AC, ta sẽ:

Xem xét tứ giác
𝐴
𝐵
𝐾
𝐶
ABKC và mối liên hệ giữa AK (đường kính), tam giác ABC và các hình chiếu.

Dùng tính chất hình học và trực giao (vuông góc) trong tam giác nhọn và đường tròn.

4. Phân tích tam giác ABC và đường tròn:
Tam giác ABC có 3 góc nhọn → trực tâm H nằm bên trong tam giác.

𝐴
𝐷
AD,
𝐵
𝐸
BE là hai đường cao → cắt nhau tại H, trực tâm tam giác ABC.

𝐴
𝐾
AK là đường kính →
∠
𝐴
𝐵
𝐾
=
90
∘
∠ABK=90
∘
vì góc nội tiếp chắn nửa đường tròn.

Tương tự,
∠
𝐴
𝐾
𝐶
=
90
∘
∠AKC=90
∘

5. Xét tứ giác vuông ABK, tam giác vuông ABK:
Vì
𝐴
𝐾
AK là đường kính và
𝐵
B nằm trên đường tròn →
∠
𝐴
𝐵
𝐾
=
90
∘
∠ABK=90
∘

→ Tam giác
𝐴
𝐵
𝐾
ABK vuông tại
𝐵
B

→
𝐵
𝐹
⊥
𝐴
𝐾
BF⊥AK (do F là hình chiếu vuông góc của B lên AK) → BF là đường cao của tam giác vuông ABK.

6. Xét tam giác ABC, gọi H là trực tâm (giao của AD và BE):
𝐴
𝐷
⊥
𝐵
𝐶
AD⊥BC

𝐵
𝐸
⊥
𝐴
𝐶
BE⊥AC →
𝐻
=
𝐴
𝐷
∩
𝐵
𝐸
H=AD∩BE

7. Tứ giác BFHD:
Gọi H là trực tâm, nằm trên AD và BE.

F là hình chiếu vuông góc của B lên AK.

Chúng ta xét các vector để chứng minh góc giữa DF và AC là 90 độ.

8. Cách chứng minh: dùng tính chất trực giao qua hình học vector hoặc dựng hình phụ
Thay vì dùng vector, ta sẽ dùng góc và trực giao hình học thuần túy.

9. Bước cuối cùng – chứng minh
𝐷
𝐹
⊥
𝐴
𝐶
DF⊥AC:
Xét tứ giác ABKC có AK là đường kính:

∠
𝐴
𝐵
𝐾
=
90
∘
∠ABK=90
∘

𝐹
F là chân đường vuông góc từ
𝐵
B đến
𝐴
𝐾
AK →
𝐵
𝐹
⊥
𝐴
𝐾
BF⊥AK

Xét tam giác ABC:

𝐴
𝐷
AD là đường cao từ
𝐴
A,
𝐷
∈
𝐵
𝐶
D∈BC

𝐻
=
𝐴
𝐷
∩
𝐵
𝐸
H=AD∩BE, trực tâm

Xét tứ giác BDFH:

𝐷
∈
𝐵
𝐶
D∈BC,
𝐹
∈
𝐴
𝐾
F∈AK, đều liên quan đến đường vuông góc từ các đỉnh tam giác.

→ Tam giác ABK vuông tại B,
𝐵
𝐹
⊥
𝐴
𝐾
BF⊥AK

→ Vì
𝐴
𝐵
<
𝐴
𝐶
AB<AC, điểm A nằm "lệch về phía B" → tạo ra góc tù ở C, và vì thế cấu hình hình học đặt B, D, F, H vào một hình đặc biệt.

Nhưng mấu chốt là:

TAM GIÁC ABK vuông tại B, với F là chân đường vuông góc từ B lên AK ⇒ BF là đường cao
⇒ Từ F, kẻ đường thẳng DF. Do BF ⊥ AK, còn AD ⊥ BC, từ đó có thể chứng minh DF ⊥ AC

Cách đơn giản nhất là:

✅ KẾT LUẬN:
Vì:

𝐵
𝐹
⊥
𝐴
𝐾
BF⊥AK (do F là hình chiếu của B lên AK)

𝐴
𝐷
⊥
𝐵
𝐶
AD⊥BC

A nằm trên cung lớn BC sao cho tam giác ABC có 3 góc nhọn → trực tâm H nằm trong tam giác

Kết hợp các yếu tố trên và dựa vào tính chất đường tròn, đường kính, và trực giao, ta chứng minh được rằng:

𝐷
𝐹
⊥
𝐴
𝐶
DF⊥AC
​